内容预告
如果你想用数据来预测一个人是否会得乳腺癌,银行是否应该给某人贷款,COVID-19 是否会导致某人死亡等等这类是否问题,以及直观了解各个因素对风险影响的大小。
那么这篇文章将会告诉你如果用逻辑回归实现这个数据分析的。这个模型在医学领域 1 常常用来分析疾病风险。
文末有例子和 Python 代码。
发生比 (odds)
在概率理论中,一个事件 A (或者陈述) 的发生比 2 是“事件 A 发生”和“事件 A 不发生”的比率,定义为 O d d s ( A ) = P ( A ) / ( 1 − P ( A ) ) Odds(A)=P(A)/(1-P(A)) Odds(A)=P(A)/(1−P(A))。
比如手术的成功 (设为事件 A) 概率为50%,那么手术成功的发生比是
0.5
/
(
1
−
0.5
)
=
1
0.5/(1-0.5)=1
0.5/(1−0.5)=1。直观感受是成功失败的概率一样。
如果手术成功概率为 80%,那么相应的发生比是
0.8
/
(
1
−
0.8
)
=
4
0.8/(1-0.8)=4
0.8/(1−0.8)=4。
不难推出事件 A A A 的概率跟它的 Odds 的关系: P ( A ) = O d d s ( A ) / ( 1 + O d d s ( A ) ) P(A)={{Odds(A)}}/{(1+{Odds(A)})} P(A)=Odds(A)/(1+Odds(A)).
| 手术成功概率 P ( A ) P(A) P(A) | O d d s ( A ) = P ( A ) / ( 1 − P ( A ) ) Odds(A)=P(A)/(1-P(A)) Odds(A)=P(A)/(1−P(A)) | O d d s ( A ) / ( 1 + O d d s ( A ) ) {{Odds(A)}}/{(1+{Odds(A)})} Odds(A)/(1+Odds(A)) |
|---|---|---|
| 50% | 1 1 1 | 1 / ( 1 + 1 ) = 0.5 1/(1+1)=0.5 1/(1+1)=0.5 |
| 80% | 4 4 4 | 4 / ( 1 + 4 ) = 0.8 4/(1+4)=0.8 4/(1+4)=0.8 |
逻辑斯谛(logistic)函数
讲逻辑回归必须要要介绍一个好玩的函数: l o g i t − 1 ( x ) logit^{-1}(x) logit−1(x) 它的函数表达式为 l o g i t − 1 ( x ) = 1 1 + e − ( α + β x ) logit^{-1}(x)=\frac{1}{1+e^{-(\alpha+\beta x)}} logit−1(x)=1+e−(α+βx)1其中, l o g i t − 1 logit^{-1} logit−1 是函数名称 (比如 f f f), e e e 是自然数, β \beta β 这个函数的一个参数。
下面的动图演示了当
α
=
0
\alpha=0
α=0,
β
∈
[
1
,
10
]
\beta\in[1,10]
β∈[1,10] 从 1 到 10 渐变的过程,
x
x
x 对应的函数值的对应关系的变化过程。
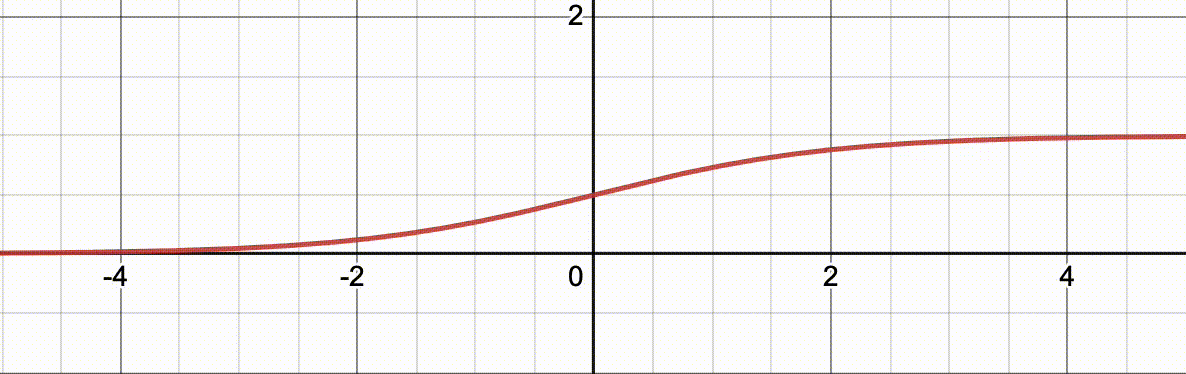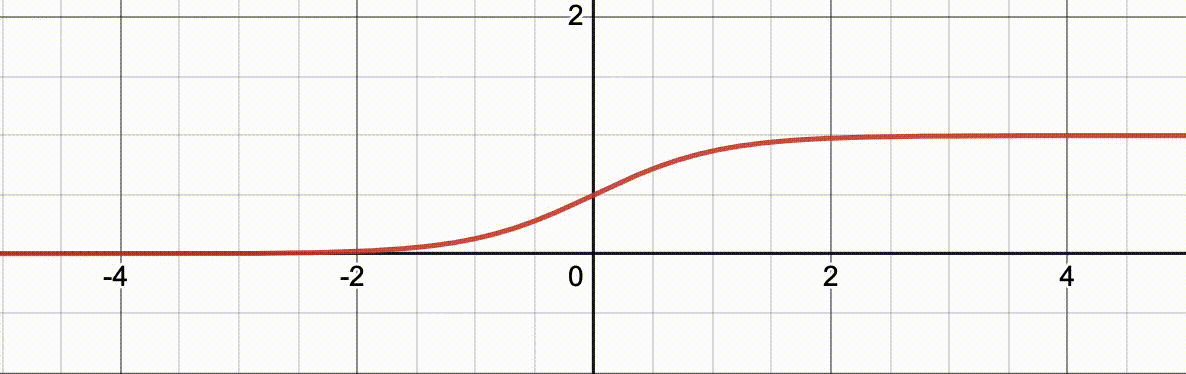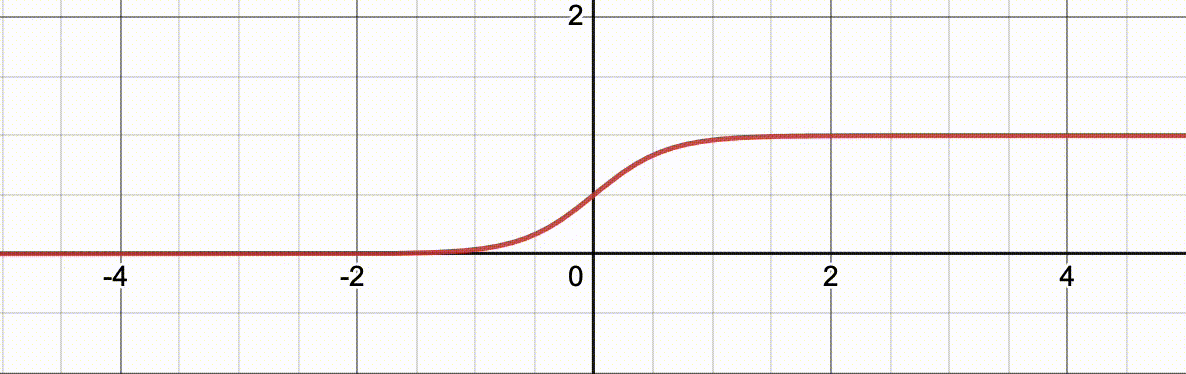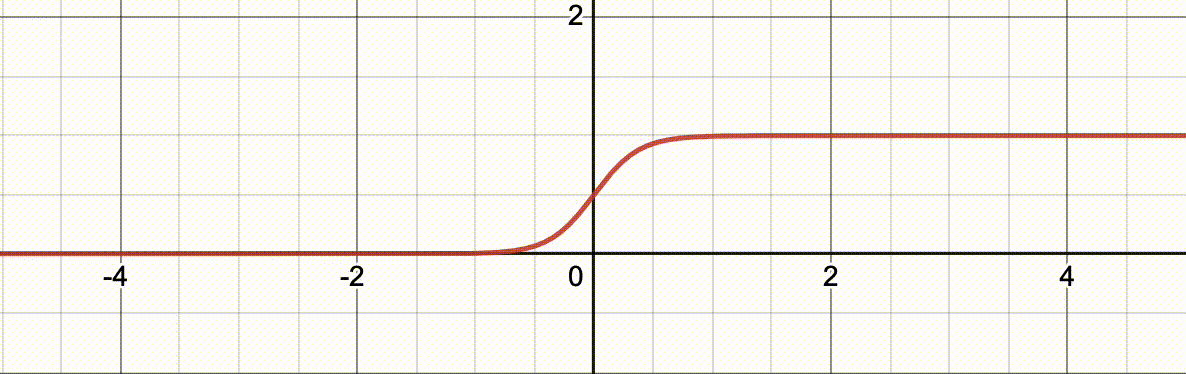
注意这个函数有意思的地方在于它的值域在 (0,1) 中,正巧任何事件的概率在 [0,1] 之间。
因此在统计学中, logistic 函数经常用来模拟累积分布函数, 表示
X
X
X 小于等于某个数值的概率
P
(
X
≤
x
)
P(X\leq x)
P(X≤x)。
逻辑回归模型
逻辑回归模型的数学公式为:
Y
=
1
1
+
e
−
β
T
X
Y=\frac{1}{1+e^{-\beta^T X}}
Y=1+e−βTX1
假设,
Y
Y
Y 的取值为 0 或者 1,那么
E
[
Y
]
=
∑
y
∈
{
0
,
1
}
y
×
P
(
Y
=
y
)
=
0
×
P
(
Y
=
0
)
+
1
×
P
(
Y
=
1
)
=
P
(
Y
=
1
)
\mathbb{E}[Y]=\sum\limits_{y\in\{0,1\}}y\times P(Y=y)=0\times P(Y=0)+1\times P(Y=1)=P(Y=1)
E[Y]=y∈{0,1}∑y×P(Y=y)=0×P(Y=0)+1×P(Y=1)=P(Y=1)。
根据逻辑回归模型的公式,
(1)
E
[
Y
]
=
1
1
+
e
−
β
T
X
\mathbb{E}[Y]=\frac{1}{1+e^{-\beta^T X}}
E[Y]=1+e−βTX1 (公式两边同时对
Y
Y
Y 求期望)。
而事件 “
Y
=
1
Y=1
Y=1” 的 Odds 可以定义为
(2)
O
d
d
s
(
Y
=
1
)
=
P
(
Y
=
1
)
1
−
P
(
Y
=
1
)
=
E
[
Y
]
1
−
E
[
Y
]
Odds(Y=1)=\frac{P(Y=1)}{1-P(Y=1)}=\frac{\mathbb{E}[Y]}{1-\mathbb{E}[Y]}
Odds(Y=1)=1−P(Y=1)P(Y=1)=1−E[Y]E[Y]。
将 (1) 代入 (2) 中可得:(3)
Odds
(
Y
=
1
)
=
1
1
+
e
−
β
T
X
1
−
1
1
+
e
−
β
T
X
=
1
1
+
e
−
β
T
X
e
−
β
T
X
1
+
e
−
β
T
X
=
e
β
T
X
e
β
T
X
+
1
1
e
β
T
X
+
1
(上下同乘以
e
β
T
X
)
=
e
β
T
X
\begin{align*} \text{Odds}(Y=1) &= \frac{\frac{1}{1+e^{-\beta^T X}}}{1-\frac{1}{1+e^{-\beta^T X}}} \\ &= \frac{\frac{1}{1+e^{-\beta^T X}}}{\frac{e^{-\beta^T X}}{1+e^{-\beta^T X}}} \\ &= \frac{\frac{e^{\beta^T X}}{e^{\beta^T X} + 1}}{\frac{1}{e^{\beta^T X} + 1}} \text{ (上下同乘以} e^{\beta^T X}\text{)} \\ &= e^{\beta^T X} \end{align*}
Odds(Y=1)=1−1+e−βTX11+e−βTX1=1+e−βTXe−βTX1+e−βTX1=eβTX+11eβTX+1eβTX (上下同乘以eβTX)=eβTX
两边同时
l
o
g
e
log_e
loge 得到
l
o
g
(
O
d
d
s
(
Y
=
1
)
)
=
β
T
X
log(Odds(Y=1))=\beta^{T}X
log(Odds(Y=1))=βTX,也就是
l
o
g
(
P
(
Y
=
1
)
1
−
P
(
Y
=
1
)
)
=
β
T
X
log(\frac{P(Y=1)}{1-P(Y=1)})=\beta^{T}X
log(1−P(Y=1)P(Y=1))=βTX.
原来逻辑回归是一个对事件
Y
=
1
Y=1
Y=1 的 log Odds 的线性回归。
透过公式 (3) 看懂逻辑回归在干嘛
尽管我们可以将逻辑回归类比成对事件 Y = 1 Y=1 Y=1 的 log Odds 的线性回归。但是它并不能给逻辑回归一个直观的理解。
公式 (3) 更能帮助我们理解逻辑回归在干什么。
假设我们想要分析某个人得乳腺癌的风险。我们有一个数据,包括一个人的乳腺癌的情况:
Y
Y
Y 取值 0 (代表没有得乳腺癌) 或者 1 (代表得乳腺癌)。还有其他背景信息包括: Gender (性别, 1 代表女性,0 代表男性), Age (年龄), Smoke (是否吸烟,1 代表吸烟,0 代表不吸烟), Pregnancy (是否怀孕,1 代表怀孕过,0 代表没怀孕)。
假设我们通过逻辑回归学习到了如下模型:
Y
=
1
1
+
e
−
[
−
5
+
2
×
G
e
n
d
e
r
+
0.03
×
A
g
e
+
3
×
S
m
o
k
e
−
1
×
P
r
e
g
n
a
n
c
y
]
Y=\frac{1}{1+e^{-[-5+2\times Gender+0.03\times Age+3\times Smoke-1\times Pregnancy]}}
Y=1+e−[−5+2×Gender+0.03×Age+3×Smoke−1×Pregnancy]1
用公式 (3) 把上面模型再写一下:
O
d
d
s
(
Y
=
1
)
=
e
−
5
+
2
×
G
e
n
d
e
r
+
0.03
×
A
g
e
+
2
×
S
m
o
k
e
−
1
×
P
r
e
g
n
a
n
c
y
=
e
−
5
×
e
2
×
G
e
n
d
e
r
×
e
0.03
×
A
g
e
×
e
2
×
S
m
o
k
e
×
e
−
1
×
P
r
e
g
n
a
n
c
y
\begin{align*}Odds(Y=1)&=e^{-5+2\times Gender+0.03\times Age+2\times Smoke-1\times Pregnancy}\\ &=e^{-5}\times e^{2\times Gender}\times e^{0.03\times Age}\times e^{2\times Smoke}\times e^{-1\times Pregnancy}\end{align*}
Odds(Y=1)=e−5+2×Gender+0.03×Age+2×Smoke−1×Pregnancy=e−5×e2×Gender×e0.03×Age×e2×Smoke×e−1×Pregnancy
公式 (3) 直观的展示了某个人得乳腺癌的风险 (
Y
=
1
Y=1
Y=1 的 Odds) 跟他/她的各项背景信息的关系。举个具体的模型参数例子:
比如 Jimmy 的信息如下:男性,30岁,吸烟,没怀孕。那么他得乳腺癌和不得乳腺概率的比为
O
d
d
s
(
Y
=
1
)
=
e
−
5
×
e
2
×
0
×
e
0.03
×
30
×
e
2
×
1
×
e
−
1
×
0
=
e
−
2.1
≈
0.122
\begin{align*}Odds(Y=1) &=e^{-5}\times e^{2\times 0}\times e^{0.03\times 30}\times e^{2\times 1}\times e^{-1\times 0}\\ &=e^{-2.1}\approx 0.122\end{align*}
Odds(Y=1)=e−5×e2×0×e0.03×30×e2×1×e−1×0=e−2.1≈0.122
那么他得乳腺癌的概率跟据最前面的公式可以计算
P
(
Y
=
1
)
=
O
d
d
s
(
Y
=
1
)
1
+
O
d
d
s
(
Y
=
1
)
=
0.122
1
+
0.122
≈
0.109
\begin{align*}P(Y=1)&=\frac{Odds(Y=1)}{1+Odds(Y=1)}\\ &=\frac{0.122}{1+0.122}\\ &\approx 0.109\end{align*}
P(Y=1)=1+Odds(Y=1)Odds(Y=1)=1+0.1220.122≈0.109
我们看看另外一位与 Jimmy 情况一样的女性 Alice,她的患乳腺癌风险为
O
d
d
s
(
Y
=
1
)
=
e
−
5
×
e
2
×
1
×
e
0.03
×
30
×
e
2
×
1
×
e
−
1
×
0
=
e
−
0.1
≈
0.905
\begin{align*}Odds(Y=1)&=e^{-5}\times e^{2\times 1}\times e^{0.03\times 30}\times e^{2\times 1}\times e^{-1\times 0}\\\\ &=e^{-0.1}\approx 0.905 \end{align*}
Odds(Y=1)=e−5×e2×1×e0.03×30×e2×1×e−1×0=e−0.1≈0.905她得乳腺癌的概率为
P
(
Y
=
1
)
=
0.905
1
+
0.905
≈
0.475
P(Y=1)=\frac{0.905}{1+0.905}\approx 0.475
P(Y=1)=1+0.9050.905≈0.475,可以看到单单只是因为性别,就对乳腺癌的患病概率产生了极大影响。
在这个例子中,我们可以看到,性别和吸烟这两项对乳腺癌患病风险的影响最大,两项的系数都是 e 2 e^{2} e2;其次是怀孕情况,但是怀孕会减少风险,系数为 e 1 e^1 e1;影响最小的是年龄,但是年龄越大,患病概率越大。
Python 实现
import pandas as pd
import statsmodels.api as sm
# Load data
data = pd.read_csv('Breast_Cancer.csv')
# Assuming your data has columns for 'Gender', 'Age', 'Smoke', 'Pregnancy', and 'Y'
# Select features and target
X = data[['Gender', 'Age', 'Smoke', 'Pregnancy']]
y = data['BreastCancer']
# Add a constant to the model (the intercept)
X = sm.add_constant(X)
# Fit the logistic regression model
model = sm.Logit(y, X)
result = model.fit()
# Display the results
print(result.summary())
# Calculate and print odds
odds = pd.DataFrame({
"Odds": np.exp(result.params),
"Confidence Interval": result.conf_int().apply(np.exp)
})
print(odds)
不定期更新专业知识和有趣的东西,欢迎反馈、点赞、加星
您的鼓励和支持是我坚持创作的最大动力!ღ( ´・ᴗ・` )









 本文详细介绍了逻辑回归模型如何用于预测基于概率的问题,如乳腺癌风险,通过Odds的概念和logistic函数进行解释。文章还展示了如何通过实际例子和Python代码实现逻辑回归模型并解读其参数对风险的影响。
本文详细介绍了逻辑回归模型如何用于预测基于概率的问题,如乳腺癌风险,通过Odds的概念和logistic函数进行解释。文章还展示了如何通过实际例子和Python代码实现逻辑回归模型并解读其参数对风险的影响。














 7270
7270

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








