现代优化算法（一）：模拟退火算法及应用举例

最新推荐文章于 2025-02-27 17:11:13 发布

wamg潇潇

最新推荐文章于 2025-02-27 17:11:13 发布

阅读量2.6w

点赞数 22

分类专栏： matlab数学建模

本文链接：https://blog.csdn.net/qq_29831163/article/details/89459183

版权

matlab数学建模专栏收录该内容

109 篇文章

订阅专栏

组合优化算法系列：

现代优化算法（一）：模拟退火算法及应用举例

现代优化算法（二）：遗传算法及应用举例

现代优化算法(三）：禁忌搜索算法

现代优化算法（四）：改进的遗传算法

现代优化算法（五）：蚁群算法

现代优化算法是 80 年代初兴起的启发式算法。这些算法包括禁忌搜索（tabu search），模拟退火（simulated annealing），遗传算法（genetic algorithms），人工神经网络（neural networks）。它们主要用于解决大量的实际应用问题。目前，这些算法在理论和实际应用方面得到了较大的发展。无论这些算法是怎样产生的，它们有一个共同的目标－求 NP-hard 组合优化问题的全局优解。虽然有这些目标，但 NP-hard 理论限制它们只能以启发式的算法去求解实际问题。

启发式算法包含的算法很多，例如解决复杂优化问题的蚁群算法（Ant Colony Algorithms）。有些启发式算法是根据实际问题而产生的，如解空间分解、解空间的限制等；另一类算法是集成算法，这些算法是诸多启发式算法的合成。

现代优化算法解决组合优化问题，如 TSP（Traveling Salesman Problem）问题，QAP （Quadratic Assignment Problem）问题，JSP（Job-shop Scheduling Problem）问题等效果很好。

模拟退火算法简介

1.2 应用举例

模拟退火算法简介

模拟退火算法得益于材料的统计力学的研究成果。统计力学表明材料中粒子的不同结构对应于粒子的不同能量水平。在高温条件下，粒子的能量较高，可以自由运动和重新排列。在低温条件下，粒子能量较低。如果从高温开始，非常缓慢地降温（这个过程被称为退火），粒子就可以在每个温度下达到热平衡。当系统完全被冷却时，终形成处于低能状态的晶体。

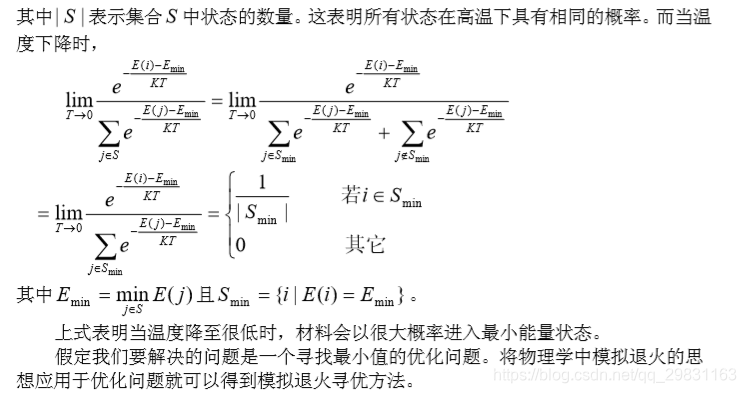
在模拟退火算法中应注意以下问题：

（1）理论上，降温过程要足够缓慢，要使得在每一温度下达到热平衡。但在计算机实现中，如果降温速度过缓，所得到的解的性能会较为令人满意，但是算法会太慢，相对于简单的搜索算法不具有明显优势。如果降温速度过快，很可能终得不到全局优解。因此使用时要综合考虑解的性能和算法速度，在两者之间采取一种折衷。

（2）要确定在每一温度下状态转换的结束准则。实际操作可以考虑当连续m 次的转换过程没有使状态发生变化时结束该温度下的状态转换。终温度的确定可以提前定为一个较小的值 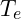$\small T_{e}$ ，或连续几个温度下转换过程没有使状态发生变化算法就结束。

（3）选择初始温度和确定某个可行解的邻域的方法也要恰当。

1.2 应用举例

例已知敌方 100 个目标的经度、纬度如表 1 所示。

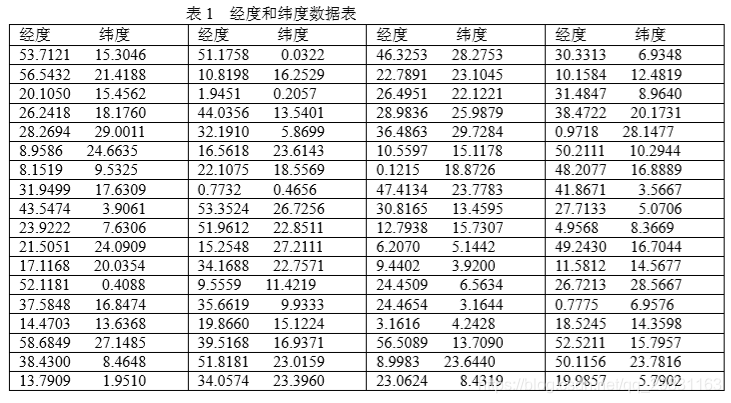
我们编写如下的 matlab 程序如下：

clc,clear 
load sj.txt    %加载敌方 100 个目标的数据，数据按照表格中的位置保存在纯文本 文件 sj.txt 中 
x=sj(:,1:2:8);x=x(:); 
y=sj(:,2:2:8);y=y(:); 
sj=[x y]; 
d1=[70,40]; 
sj=[d1;sj;d1]; 
sj=sj*pi/180; %距离矩阵 
d 
d=zeros(102); 
for i=1:101     
    for j=i+1:102         
        temp=cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2));
        d(i,j)=6370*acos(temp);     
    end 
end 
d=d+d'; 
S0=[];Sum=inf; 
rand('state',sum(clock)); 
for j=1:1000     
    S=[1 1+randperm(100),102];     
    temp=0; 
    for i=1:101         
        temp=temp+d(S(i),S(i+1));     
    end     
    if temp<Sum         
        S0=S;Sum=temp;     
    end 
end 
e=0.1^30;L=20000;at=0.999;T=1; 
%退火过程 
for k=1:L    %产生新解 
    c=2+floor(100*rand(1,2)); 
    c=sort(c); c1=c(1);c2=c(2);   %计算代价函数值   
    df=d(S0(c1-1),S0(c2))+d(S0(c1),S0(c2+1))-d(S0(c1-1),S0(c1))-d(S0(c2),S0(c2+1)); %接受准则   
    if df<0   
        S0=[S0(1:c1-1),S0(c2:-1:c1),S0(c2+1:102)];         
        Sum=Sum+df;   
    elseif exp(-df/T)>rand(1)   
        S0=[S0(1:c1-1),S0(c2:-1:c1),S0(c2+1:102)];   
        Sum=Sum+df;   
    end   
    T=T*at;    
    if T<e        
        break;    
    end 
end  
% 输出巡航路径及路径长度 
S0,Sum

计算结果为 44 小时左右。其中的一个巡航路径如图 1 所示。