阿伦(Allan)方差分析广泛应用于惯性器件的随机误差建模,常见的有陀螺误差分析。我需要对光纤陀螺的随机误差进行分析,故对阿伦方差的的原理以及python代码实现进行了整理,其中理论参考严恭敏老师的《惯性仪器测试与数据分析》第八章,python代码参考Allen B. Downey的《Think DSP》1
统计学中用均值和方差描述随机变量,但是,Allan 在1966年分析铯原子频标的频率稳定度时发现经典方差随着测量时间的增长而发散,为了解决该问题,提出了阿伦方差(Allan Variance, AVAR)分析法,后来IEEE在1971年正式推荐Allan方差作为频率频率稳定度的时域分析方法,后来被广泛应用于惯性器件的分析中。
随机信号Allan方差的物理意义及应用本质上源于它和功率谱之间的关系。故本文分为三个部分,1.功率谱的幂律模型以及python代码实现 2. 经典方差和Allan方差 3. 陀螺随机漂移误差的Allan分析以及python代码实现。
功率谱的幂律模型以及python代码实现
数学定义的连续时间白噪声 w ( t ) w(t) w(t),其在整个频率轴 f ∈ ( − ∞ , ∞ ) f\in (-\infty,\infty) f∈(−∞,∞)上功率谱都为常值 S w t S_{wt} Swt ,并且仅在 t = 0 t=0 t=0时自相关函数取值无限大,其他任何间隔时间下均不相关。在实际系统中,如果处理信号的带宽远远小于噪声源的带宽,则可以对带宽噪声源的功率谱进行合理扩展,以简化系统分析,通常数学上定义的白噪声是实际物理系统在感兴趣频段上平直功率谱外推后的理想化建模。
对连续时间信号 x ( t ) x(t) x(t)及其傅里叶变换 X ( j f ) X(jf) X(jf),根据时域微分或者积分性质有
C T F T [ x ′ ( t ) ] = j 2 π f ⋅ X ( j f ) CTFT[x\prime(t)]=j2\pi f \cdot X(jf) CTFT[x′(t)]=j2πf⋅X(jf)
C T F T [ ∫ − ∞ t x ( τ ) d τ ] = π X ( 0 ) δ ( f ) + 1 j 2 π f X ( j f ) = 1 j 2 π f X ( j f ) ( X ( 0 ) = 0 ) CTFT[\int\limits_{-\infty}^{t}x(\tau)d\tau]=\pi X(0)\delta(f) + \frac{1}{j2\pi f}X(jf) = \frac{1}{j2\pi f}X(jf)(X(0)=0) CTFT[−∞∫tx(τ)dτ]=πX(0)δ(f)+j2πf1X(jf)=j2πf1X(jf)(X(0)=0)
由此可得,积分和微分运算均为线性变换运算,可将运算结果看作是原信号经过线性系统之后的输出。如果将白噪声 w ( t ) w(t) w(t)输入微分线性系统 H ( j f ) = j 2 π f H(jf)=j2\pi f H(jf)=j2πf(在数学上白噪声不可微,这里只是形式上)则系统输出随机微分和积分信号的功率谱为:
S w t ′ = ( 2 π f ) 2 S w t S_{wt\prime}=(2\pi f)^2S_{wt} Swt′=(2πf)2Swt
S ∫ w t ( f ) = ( 2 π f ) − 2 S w t S_{\int wt}(f)=(2\pi f)^{-2}S_{wt} S∫wt(f)=(2πf)−2Swt
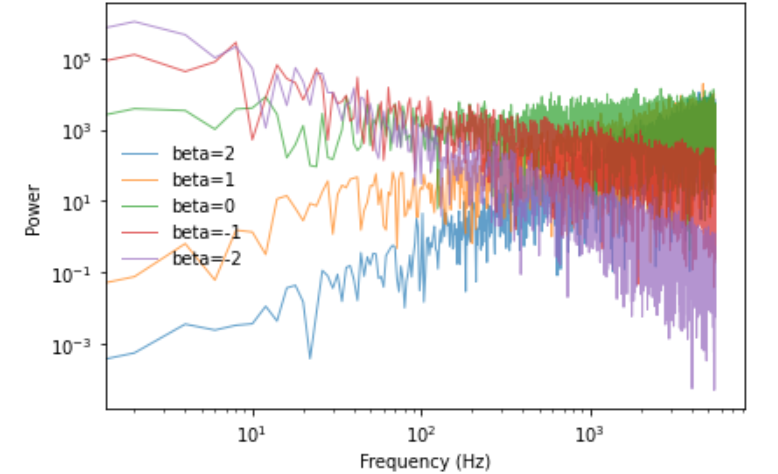
容易看出,微分系统具有高通滤波器特性,白噪声随机微分后,高频分量增强。积分系统具有低通滤波特性,低频分量增强。将白噪声进行一次随机微分和积分,分别得到了与 f 2 f^2 f2和 f − 2 f^{-2} f−2成比例的功率谱,如果对白噪声进行 k k k次随机积分或者微分,所得功率谱将具有幂次 S k = A k F 2 k ( k = 0 , ± 1 , ± 2... ) S_k = A_k F^{2k}(k=0,\pm1,\pm2 ...) Sk=AkF2k(k=0,±1,±2...)形式,如果绘制log-log图,则有 l o g 10 S k = l o g 10 A k + 2 k l o g 10 f log_{10}S_{k} = log_{10}A_k + 2klog_{10}f log10Sk=log10Ak+2klog10f ,其为斜率是 2 k 2k 2k的线性功率谱。在实际的物理系统中,除了斜率为 2 k 2k 2k的功率谱外,在大量电子设备中普遍存在着 1 / f 1/f 1/f噪声。下图给出了几种斜率的功率谱,其中 f 0 ( b e t a = 0 ) f^0(beta=0) f0(beta=0)对应白噪声序列, f − 2 ( b e t a = − 2 ) f^{-2}(beta=-2) f−2(beta=−2)对应白噪声序列的累计(即随机游走序列), f 2 ( b e t a = 2 ) f^2(beta=2) f2(beta=2)对应白噪声序列的差分, f − 1 ( b e t a = − 1 ) f^{-1}(beta=-1) f−1(beta=−1)和 f 1 ( b e t a = 1 ) f^1(beta=1) f1(beta=1)通过对频域直接处理得到。
下面对python代码实现进行说明,需要将thinkdsp.py文件放在运行目录中,文件获取后台回复阿伦方差
import numpy as np
import matplotlib.pyplot as plt
from thinkdsp import decorate #导入作图帮助函数
from thinkdsp import BrownianNoise # 引入随机游走噪声序列
signal = BrownianNoise()
wave = signal.make_wave(duration=0.5, framerate=11025) # 将随机游走生成波
wave.make_audio() # 在jupyter中会生成音频文件,可以试听
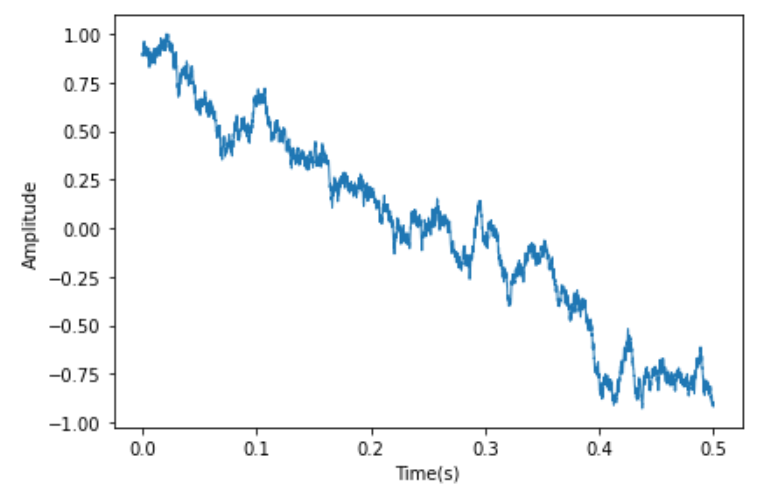
# 可以在时域看看其序列
wave.plot(linewidth = 1)
decorate(xlabel='Time(s)',
ylabel='Amplitude')
# 对随机游走序列进行频域分析,并且作图
spectrum = wave.make_spectrum()
spectrum.plot_power(linewidth=0.5)
decorate(xlabel='Frequency (Hz)',
ylabel='Power')
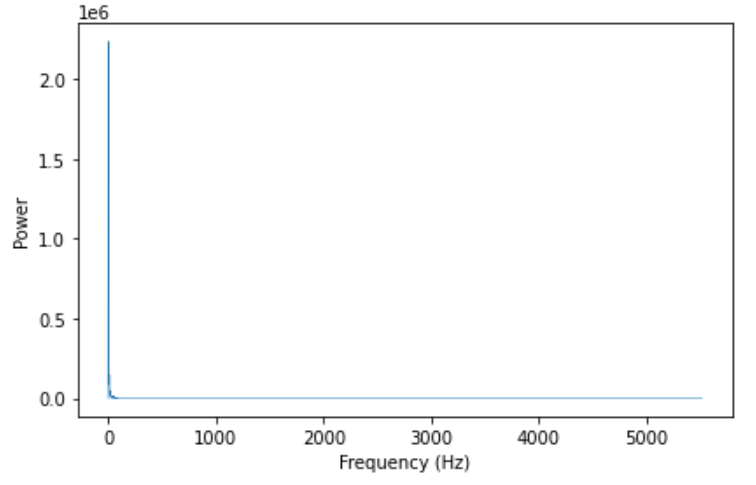
# 由于其低频分量占比较多,故采用loglog图
spectrum.hs[0] = 0 # log 0 不存在,故修改
spectrum.plot_power(linewidth=0.5)
loglog = dict(xscale='log', yscale='log')
decorate(xlabel='Frequency (Hz)',
ylabel='Power',
**loglog)spectrum.hs[0] = 0
spectrum.plot_power(linewidth=0.5)
loglog = dict(xscale='log', yscale='log')
decorate(xlabel='Frequency (Hz)',
ylabel='Power',
**loglog)
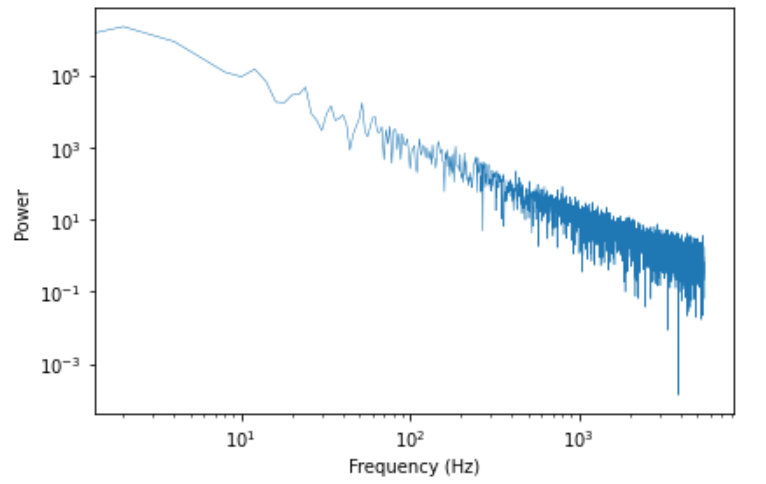
result = spectrum.estimate_slope() # 对功率谱斜率估计
[out]: -1.7954213807211257 #接近-2
其他斜率的功率生成与上述随机游走类似,故不在赘述。需要注意的是
BlueNoise和PinkNoise分别表示斜率区间为(0,2)和(-2,2),其中BlueNoise是我自己改的,如果引用作者源代码的化可能会报错- 由于代码是参考的音乐的处理方式,上述的斜率和和参数
beta是相反的,如果不确定对应关系,可以通过斜率估算函数得到对应的斜率。 - 建议对源码进行阅读。
如果若干个随机过程 X a X_a Xa之间相互独立且设总和 X = Σ X a X=\Sigma X_a X=ΣXa,则有 P S D [ X ] = Σ P S D [ X a ] PSD[X] = \Sigma PSD[X_a] PSD[X]=ΣPSD[Xa] 。若 X a X_a Xa为线性功率谱,即 P S D [ X a ] = h a f a PSD[X_a]=h_af^a PSD[Xa]=hafa,并且实际应用中 a a a取 − 2 , − 1 , 0 , 1 , 2 -2,-1,0,1,2 −2,−1,0,1,2,则随机过程 f − S f-S f−S为
l o g 10 S = l o g 10 ( Σ h a f a ) ≈ Σ ( l o g 10 h a + a l o g 10 f ) , f a L < f < f a H log_{10}S = log_{10}(\Sigma h_a f^a) \approx \Sigma(log_{10}h_a + alog_{10}f), f_{aL}<f<f_{aH} log10S=log10(Σhafa)≈Σ(log10ha+alog10f),faL<f<faH
对理想的幂律谱噪声按不同比例进行混合,得到的s-log可以大概看到不同斜率的占比。
from thinkdsp import Wave
def get_sum_wave(K, wave_red_noise=wave_red_noise, wave_pink_noise=wave_pink_noise, wave_white_noise=wave_white_noise, wave_blue_noise=wave_blue_noise, wave_purple_noise=wave_purple_noise):
wave_sum_ys = wave_red_noise.ys*K[0] + wave_pink_noise.ys*K[1] + wave_white_noise.ys*K[2] + wave_blue_noise.ys*K[3] + wave_purple_noise.ys*K[4]
wave_sum = Wave(wave_sum_ys, wave_white_noise.ts, wave_white_noise.framerate)
return wave_sum
K1 = [10,0,10,0,10]
K2 = [10,0,0,0,10]
spectrum_sum1 = get_sum_wave(K1).make_spectrum()
spectrum_sum2 = get_sum_wave(K2).make_spectrum()
spectrum_sum1.plot_power(linewidth=0.5, label='K1')
spectrum_sum2.plot_power(linewidth=0.5, label='K2')
loglog = dict(xscale='log', yscale='log')
decorate(xlabel='Frequency (Hz)',
ylabel='Power',
**loglog,
ylim=(1e-1,1e8))
结果如下图所示
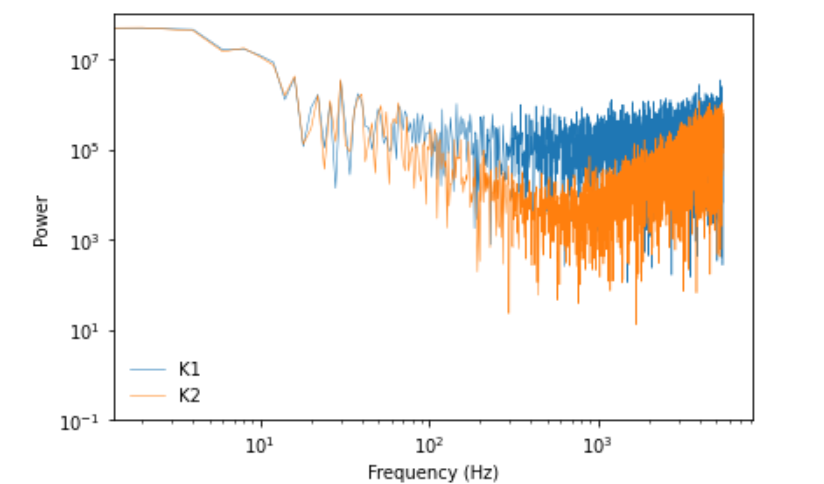
K1相比于K2在于有更多的白噪声分量,表现出结果就是在倒角处的斜率更加接近平行(白噪声斜率为0)
经典方差和Allan方差
频标输出的准周期信号通用模型为:
u
(
t
)
=
[
A
0
+
A
(
t
)
]
s
i
n
[
2
π
v
0
t
+
ϕ
(
t
)
]
u(t)=[A_0+A(t)]sin[2\pi v_0t + \phi(t)]
u(t)=[A0+A(t)]sin[2πv0t+ϕ(t)]
式中
A
0
,
v
0
A_0,v_0
A0,v0分别为信号输出的理想幅值和标称频率,
A
(
t
)
,
ϕ
(
t
)
A(t),\phi(t)
A(t),ϕ(t)分别为幅值起伏的相位抖动,一般情况下忽略
A
(
t
)
≪
A
0
A(t)\ll A_0
A(t)≪A0,分析时忽略
A
(
t
)
A(t)
A(t)的影响,信号的瞬时频率为相位相对时间的导数,即
v
(
t
)
=
1
2
π
⋅
d
[
2
π
v
0
t
+
ϕ
(
t
)
]
d
t
=
v
0
+
1
2
π
⋅
d
ϕ
(
t
)
d
t
v(t)=\frac{1}{2\pi}\cdot \frac{d[2\pi v_0 t + \phi(t)]}{dt}=v_0 + \frac{1}{2\pi}\cdot \frac{d\phi(t)}{dt}
v(t)=2π1⋅dtd[2πv0t+ϕ(t)]=v0+2π1⋅dtdϕ(t)
定义瞬时相对频率偏差:
y
(
t
)
=
v
(
t
)
−
v
0
v
0
=
1
2
π
v
0
⋅
d
ϕ
(
t
)
d
t
y(t) = \frac{v(t)-v_0}{v_0}=\frac{1}{2\pi v_0}\cdot \frac{d\phi(t)}{dt}
y(t)=v0v(t)−v0=2πv01⋅dtdϕ(t)
在实际情况中,通常无法测得频率的瞬间偏差值,而只能测一段时间
[
t
i
,
t
i
+
τ
]
[t_i, t_i + \tau]
[ti,ti+τ]内的平均值
y
i
(
τ
)
y_i(\tau)
yi(τ),即
y
i
(
τ
)
=
1
τ
∫
t
i
t
i
+
τ
y
(
t
)
d
t
y_i(\tau) = \frac{1}{\tau}\int \limits^{t_i + \tau}_{t_i}y(t)dt
yi(τ)=τ1ti∫ti+τy(t)dt
其中
τ
\tau
τ为平均时间,也就是平均频率的取样时间,经典方差也就是
y
i
2
y_i^2
yi2,当无间隔取样时有
<
y
i
2
(
τ
)
>
=
2
∫
0
∞
S
y
(
f
)
s
i
n
2
(
π
f
τ
)
(
π
f
τ
)
2
d
f
<y^2_i(\tau)>=2\int \limits^{\infty}_{0}S_y(f) \frac{sin^2(\pi f \tau)}{(\pi f \tau)^2}df
<yi2(τ)>=20∫∞Sy(f)(πfτ)2sin2(πfτ)df
其中
S
y
(
f
)
S_y(f)
Sy(f)为功率谱函数,具体推导过程参考严老师《惯性仪器测试与数据分析》
由上分析可得,平均时间为 τ \tau τ的时域经典方差 y i 2 ( τ ) y^2_i(\tau) yi2(τ)表示频率偏差信号 y ( t ) y(t) y(t)通过滤波器 H ( j f ) H(jf) H(jf)后的平均功率输出,其中 H ( j f ) H(jf) H(jf)为
H ( j f ) = s i n ( π f τ ) π f τ = S a ( π f τ ) H(jf)=\frac{sin(\pi f \tau)}{\pi f \tau}=Sa(\pi f \tau) H(jf)=πfτsin(πfτ)=Sa(πfτ)
若 y ( t ) y(t) y(t)非平稳,如果含有趋势项(均值时变但方差定常)或者表现为维纳过程,这是 y i ( τ ) y_i(\tau) yi(τ)也将包含趋势项或表现为随机游走过程,对于非平稳信号的功率谱 S y ( f ) S_y(f) Sy(f)在零频率附近为无穷大,且不可积,这样导致经典方差 y i 2 ( τ ) y^2_i(\tau) yi2(τ)也趋于无穷,因此对于非平稳频标,不能再使用经典方法来表示频率稳定性。
现定义Allan方差如下:
σ
y
2
(
τ
)
=
1
2
<
[
y
i
+
1
(
τ
)
−
y
i
(
τ
)
]
2
>
\sigma^2_y(\tau)=\frac{1}{2} <[y_{i+1}(\tau)-y_i(\tau)]^2>
σy2(τ)=21<[yi+1(τ)−yi(τ)]2>
略去推理过程可以得到
σ
y
2
(
τ
)
=
4
∫
0
∞
S
y
(
f
)
s
i
n
4
(
π
f
τ
)
(
π
f
τ
)
2
d
f
\sigma^2_y(\tau)=4\int \limits^{\infty}_{0}S_y(f) \frac{sin^4(\pi f \tau)}{(\pi f \tau)^2}df
σy2(τ)=40∫∞Sy(f)(πfτ)2sin4(πfτ)df
同理,采样时间为
τ
\tau
τ的时域阿伦方差
σ
i
2
(
τ
)
\sigma^2_i(\tau)
σi2(τ)表示频率偏差信号
y
(
t
)
y(t)
y(t)通过滤波器
H
A
(
j
f
)
H_A(jf)
HA(jf)后的平均功率输出,其中
H
A
(
j
f
)
H_A(jf)
HA(jf)为
H
A
(
j
f
)
=
−
j
2
s
i
n
2
(
π
f
τ
)
π
f
τ
=
S
a
(
π
f
τ
)
×
[
−
j
2
s
i
n
(
π
f
τ
)
]
H_A(jf)=-j \sqrt2 \frac{sin^2(\pi f \tau)}{\pi f \tau}=Sa(\pi f \tau)\times [-j\sqrt2 sin(\pi f \tau)]
HA(jf)=−j2πfτsin2(πfτ)=Sa(πfτ)×[−j2sin(πfτ)]
其中
S
a
(
π
f
τ
)
Sa(\pi f \tau)
Sa(πfτ)为低通滤波器,对应均值采样过程,
[
−
j
2
s
i
n
(
π
f
τ
)
]
[-j\sqrt2 sin(\pi f \tau)]
[−j2sin(πfτ)]为带通滤波器,对应差分
y
i
+
1
(
τ
)
−
y
i
(
τ
)
y_{i+1}(\tau)-y_i(\tau)
yi+1(τ)−yi(τ)过程。所以Allan方差计算的实质是使信号通过一个带通滤波器,然后做某种时间统计平均
[
⋅
]
2
[ \cdot ]^2
[⋅]2
通过与上一部分的幂律谱函数结合,则可以得到Allan方差是一种对功率谱进行加权后的自相关,加权函数为 ∣ H A ( j f ) ∣ 2 |H_A(jf)|^2 ∣HA(jf)∣2。
陀螺随机漂移误差的Allan分析以及python代码实现
综合上述的分析,可以得到,如果要对陀螺随机漂移误差进行阿伦方差建模,则首先需要得到影响陀螺随机漂移噪声源的功率谱,带入上节公式(8)得到对应噪声的阿伦方差,最后根据幂律谱模型进行建模。
本节对影响陀螺的噪声源物理背景进行说明,最后将阿伦方差整理为表格,略去推理过程,推理过程参见教材。
-
量化噪声(Quantization Noise,QN)
量化噪声是一切量化操作所固有的噪声,只要进行数字量化编码采样,传感器输出的理想值与量化值之间就必然会存在微笑差别,量化噪声代表了传感器检测的最小分辨率。
-
角度随机游走(Angular Random Walk, ARW)
角度随机游走是宽带角速率白噪声积分的结果,即陀螺从零时刻其累积的总角增量误差表现为随机游走,而每一时刻的等效角速率误差表现为白噪声。
-
角速率随机游走(Rate Random Walk, RRW)
角速率随机游走是宽带叫角加速率白噪声积分的结果,即陀螺角加速率误差表现为白噪声,而角速率误差表现为随机游走。
-
零偏不稳定性噪声(Bias Instability, BI)
零偏不稳定性噪声又称为闪变噪声或 1 / f 1/f 1/f噪声,顾名思义,其功率谱密度与频率成反比。
-
速率斜坡(Rate Ramp, RR)
陀螺角速率输出随时间缓慢变化,对于光纤陀螺来说,环境温度变化会引起角速率的线性变化。
噪声源的阿伦方差分析如下
| 噪声类型 | 功率谱 S Ω ( f ) S_\Omega(f) SΩ(f) | Allan方差 σ A 2 ( τ ) \sigma^2_A(\tau) σA2(τ) | 与 τ = 1 \tau=1 τ=1交点纵坐标 | 斜率 |
|---|---|---|---|---|
| 量化噪声 | τ 0 Q 2 ( 2 π f ) 2 \tau_0Q^2(2\pi f)^2 τ0Q2(2πf)2 | 3 Q 2 / τ 2 3Q^2/\tau^2 3Q2/τ2 | 3 Q \sqrt3 Q 3Q | − 1 -1 −1 |
| f噪声 | F ( 2 π f ) F(2\pi f) F(2πf) | 3 F ln ( e π f H τ ) π τ 2 \frac{3F \ln {(e \pi f_H \tau)}}{\pi \tau^2} πτ23Fln(eπfHτ) | 3 F ln ( e π f H ) / π \sqrt{3F \ln(e \pi f_H)/\pi} 3Fln(eπfH)/π | |
| 角度随机游走 | N 2 N^2 N2 | N 2 / τ N^2/\tau N2/τ | N N N | − 1 / 2 -1/2 −1/2 |
| 零偏不稳定性 | B 2 / ( 2 π f ) B^2/(2\pi f) B2/(2πf) | 4 B 2 / 9 4B^2/9 4B2/9 | 2 B / 3 2B/3 2B/3 | 0 0 0 |
| 角速率随机游走 | K 2 / ( 2 π f ) 2 K^2/(2 \pi f)^2 K2/(2πf)2 | K 2 τ / 3 K^2\tau/3 K2τ/3 | K / 3 K/\sqrt3 K/3 | 1 / 2 1/2 1/2 |
| 速率斜坡 | − − − --- −−− | R 2 τ 2 / 2 R^2\tau^2/2 R2τ2/2 | R / 2 R/\sqrt2 R/2 | 1 1 1 |
根据上表以及幂律谱模型,可以得到陀螺的Allan 方差模型为
σ
A
2
(
τ
)
=
σ
Q
N
2
(
τ
)
+
σ
A
R
W
2
(
τ
)
+
σ
B
I
2
(
τ
)
+
σ
R
R
W
2
(
τ
)
+
σ
R
R
2
(
τ
)
\sigma^2_A(\tau) = \sigma^2_{QN}(\tau)+\sigma^2_{ARW}(\tau)+\sigma^2_{BI}(\tau)+\sigma^2_{RRW}(\tau)+\sigma^2_{RR}(\tau)
σA2(τ)=σQN2(τ)+σARW2(τ)+σBI2(τ)+σRRW2(τ)+σRR2(τ)
将上表的第三列带入得:
σ
A
2
(
τ
)
=
3
Q
2
τ
2
+
N
2
τ
+
4
B
2
9
+
K
2
τ
3
+
R
2
τ
2
2
=
Σ
k
=
−
2
2
A
k
τ
k
\sigma^2_A(\tau) = \frac{3Q^2}{\tau^2}+\frac{N^2}{\tau}+\frac{4B^2}{9}+\frac{K^2\tau}{3}+\frac{R^2\tau^2}{2}=\Sigma^2_{k=-2}A_k\tau^k
σA2(τ)=τ23Q2+τN2+94B2+3K2τ+2R2τ2=Σk=−22Akτk
对实际数据进行阿伦方差,需要获得一组采样间隔为 τ 0 \tau_0 τ0内的平均角速率值,通常取 τ 0 = 1 \tau_0=1 τ0=1。
python代码如下
def get_allen(y, tau0=1):
N = len(y)
NL = N
Tau = [] # 保存不同的tau
Sigma = [] # 保存不同tao下的阿伦方差值
Err = []
for k in np.arange(1, 1000):
sigma_k = np.sqrt(1/(2*(NL-1)) * np.sum(np.power(y[1:NL]-y[0:NL-1], 2))) #Allan的时域表达式
Sigma.append(sigma_k)
tau_k = 2 ** (k-1) * tau0 #将取样时间加倍, tau2 = 2tau1
Tau.append(tau_k)
err = 1 / np.sqrt(2* (NL-1))
Err.append(err)
NL = np.floor(NL/2)
NL = int(NL)
if NL < 3:
break
y = 1/2 * (y[0:2*NL:2] + y[1:2*NL:2]) # 对应的序列长度减半
return Sigma, Tau
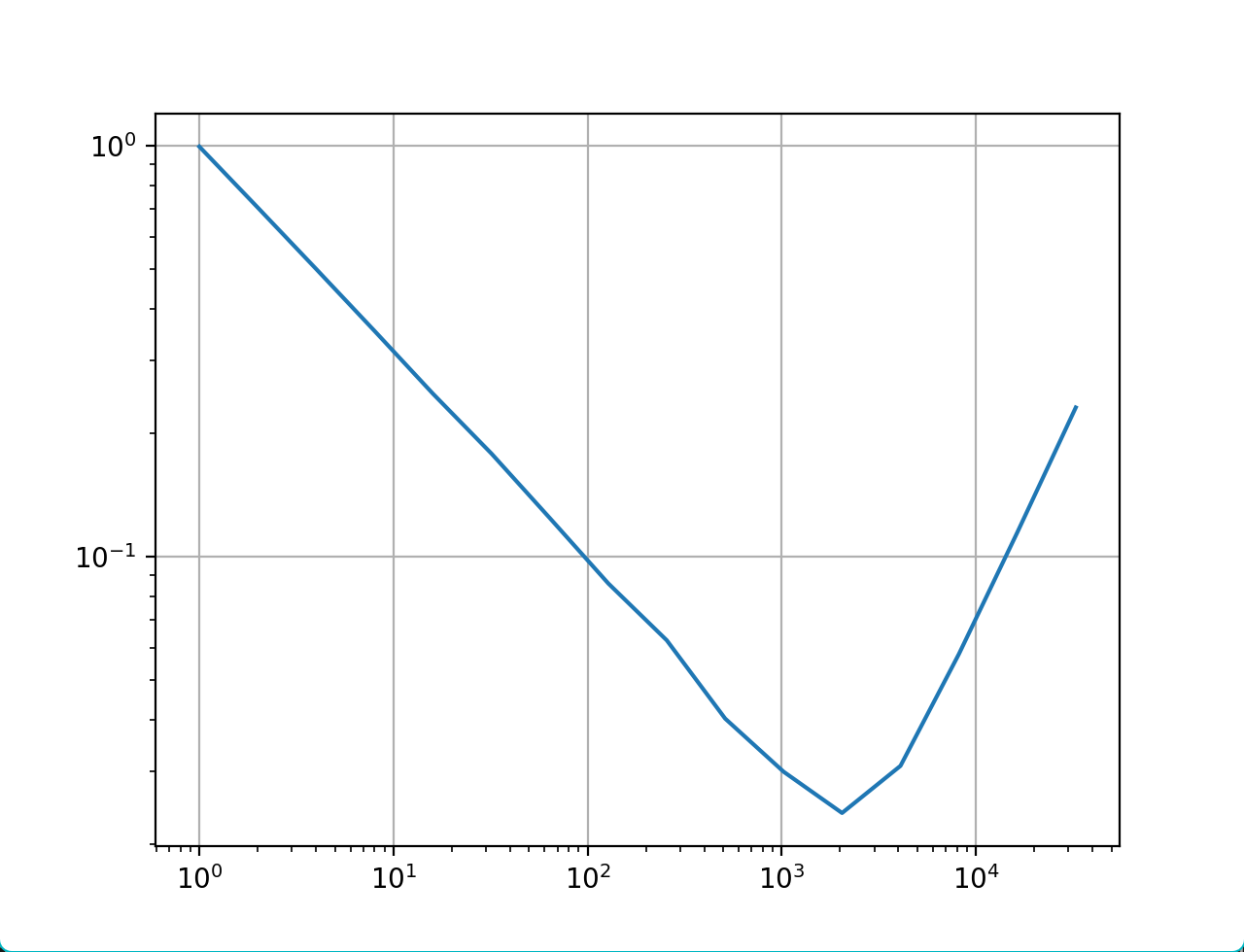
对随机数进行Allan分析得到如下结果
if __name__ == '__main__':
data_size_ex = 5
y = np.random.standard_normal((10**data_size_ex),) + (10 ** -data_size_ex) * np.arange(1,10**data_size_ex + 1)
fig, ax = plt.subplots()
Sigma, Tau = get_allen(y)
ax.set_xscale("log")
ax.set_yscale("log")
ax.set_adjustable("datalim")ax.plot(Tau, Sigma)
ax.grid()
plt.show()






















 842
842











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








