文章目录
- 1. 标度(Scale)与标度律
- 2. 缩放(Scaling)
- 3. 标度不变性
- 3.1 标度不变(Scale-invariant)曲线和自相似性(self-similarity)
- 3.2 随机过程中的标度不变性
- 3.3 经典场论中的标度不变性
- 3.4 量子场论中的标度不变性
- 3.5 相变
- 3.6 标度不变性的其他例子
- 3.7 标度空间(Scale space)
- 3.8 标度不变特征变换(Scale-invariant feature transform)
- 3.9 普适性(Universality)
- 3.10 普适类(Universality class)
- 3.11 临界现象
- 4. 无标度网络(Scale-free network)
1. 标度(Scale)与标度律
在感官检验中,标度方法是感官体验的量化方式,通过这种数字化的处理,感官评价可以成为基于统计分析、模型、预测等理论的定量科学。
标度方法广泛应用于需要量化感觉、态度或喜好倾向性等各种场合。标度技术基于感觉强度的心理物理学模型。即增强物理刺激的能量或增加食品组分的浓度或含量,会导致其在感觉、视觉、嗅觉或味觉方面有多大程度的增强。
从感官检验的定义中我们知道,它是一门度量的科学,度量是将感官体验进行量化的关键一步, 在此基础上才能将数据进行统计分析。标度法中既使用数据来表达样品性质的强度(甜度、硬度、柔软度),也是用词汇来表达对该性质的感受(太软、正合适、太硬)。如果使用词汇,应该将词汇和数字对应起来,比如非常喜欢 =9,非常不喜欢 =1,这样就可以将这些数据进行统计分析。
1.1 标度种类
有 4 种对事件的标度种类,通常是指名义标度、序级标度、等距标度和比率标度。这几种标度是根据测量理论中测量水平提出的,适用于各个水平的各类统计分析和不同的建模水平。
1.1.1 名义标度
名义标度中,对于事件的赋值仅仅是作为标记。数值赋值仅仅是用于分析的一个标记、类项或种类,不反应序列特征。对这类数据的适当分析是进行频率计算并报告的结果。
1.1.2 序级标度
序级标度中,赋值是为了对产品的一些特性、品质或观点(如偏爱)标示排列的顺序,该方法赋给产品的数值增加标示感官体验的数量或强度增加。
1.1.3 等距标度
当反应的主观间距相等时会出现等距标度。在该标度水平下,赋值的数据可以表示实际的差别程度。那么这种差别程度就是可以比较的,成为等距水平测量。
1.1.4 比率标度
在比率标度下,0 点不是任意的,而是数值反映了比例。
1.2 常用标度方法
常用的标度方法有第三种,最古老也是最广为使用的标度方法是类项标度,评价员根据特定而有限的反应,将数值赋予察觉到的感官刺激。第二种的方法与此相应,是量值估计法,这种方法评价员可以对感觉赋予任何数值来反映其比率。第三种常用的方法是线性标度法。该方法是评价员采用在一条线上做标记来评价感觉强度或喜爱程度。
1.3 标度律
在日常的直觉中,人们习惯于用几何相似地放大(或缩小)的倍数去推论其后果,譬如,一个人身体高了50%,做衣服用的布料也要多50%。曾经流传过一种说法:跳蚤可以跳了一米高,若它长得像人那样大,就能跳一千多米高。这里都错误地按几何线度放大的倍数去推算其它某种后果。对于一定几何形状的物体,若其几何线度为 l l l, l l l 改变时,其它因素按怎样的规律变化?这类规律可称之为标度律。上述物体的表面积 S ∝ l 2 S\propto l^{2} S∝l2,体积 V ∝ l 3 V\propto l^{3} V∝l3,这是最基本的标度律,它们是由量纲关系决定的。所以身高 1.5 1.5 1.5 倍,费布料多 ( 1.5 ) 2 = 2.25 (1.5)^{2}=2.25 (1.5)2=2.25 倍,这里的标度律是布料面积 ∝ l 2 \propto l^{2} ∝l2。跳蚤体内储存的能量 E ∝ 体重 E\propto\text{体重} E∝体重,设密度不变,则 E ∝ 体积 ∝ l 3 E\propto\text{体积}\propto l^{3} E∝体积∝l3。另一方面,跳到高度 h h h 所需重力势能 m g h ∝ 体重 ∝ l 3 mgh\propto\text{体重}\propto l^{3} mgh∝体重∝l3。所以这里的标度律是 h ∝ l 0 h\propto l^{0} h∝l0(不变),即像人那样大的跳蚤也只能跳一米高。
伽利略在他第二本名著《两种新科学的对话》中记载了威尼斯造船厂一位有经验工匠的话:“在最大的船只下水时必须格外注意,以避免大船在它们自身的巨大重量下发生开裂的危险。”这段话引发了书中对话者的争论,问题的实质是,将小船的设计按比例几何相似地按比例放大,造出的船是否变得不结实了?用量纲来分析,这是显然的。 船的重量(包括自重与载荷) ∝ 体积 ∝ l 3 \text{船的重量(包括自重与载荷)}\propto\text{体积}\propto l^{3} 船的重量(包括自重与载荷)∝体积∝l3,而船的骨架的横截面积 S ∝ l 2 S\propto l^{2} S∝l2,从而这里的标度律是 单位面积上的负荷 ∝ l \text{单位面积上的负荷}\propto l 单位面积上的负荷∝l,船越大,单位面积上的负荷越大,开裂的危险也就越大。这个道理可以用到其它许多地方,譬如马从两倍于它身高的地方跌下来会摔断骨头,而猫可以从五六倍于自己身高的地方跳下来安全无恙,老鼠从天花板上跌落下来(这相当于它身高的几十倍),什么危险也没有。大象粗壮的四条腿,与其它小型动物的腿是不成比例的。鲸鱼这样大的哺乳动物只能生活在海里,在岸上搁浅,失去了水的浮力,它们就会被自身的重量压死。
寻找正确的标度律,对于许多实际问题是很重要的。例如用缩小的模型去模拟桥梁、水坝、乃至飞机,都需要用正确的标度律来指导,而正确的标度律要靠量纲分析来得到。
2. 缩放(Scaling)

图 Sierpinski 三角形的每次迭代都包含与下一次迭代相关的三角形,比例因子为 1/2。
在仿射几何(affine geometry)中,均匀缩放(uniform scaling)(或各向同性缩放(isotropic scaling))是一种线性变换,它通过在所有方向上相同的比例因子放大(增加)或缩小(缩小)对象。均匀缩放的结果与原始结果相似(在几何意义上)。通常允许比例因子为 1,因此全等形状也被归类为相似形状。例如,在放大或缩小照片时,或者在创建建筑物、汽车、飞机等的比例模型时,会发生统一缩放。
更一般的是针对每个轴方向使用单独的比例因子进行缩放。当至少一个缩放因子与其他缩放因子不同时,获得非均匀缩放(各向异性缩放);一种特殊情况是定向缩放或拉伸(在一个方向上)。非均匀缩放会改变对象的形状;例如,如果正方形的边不平行于缩放轴(保留与轴平行的线之间的角度,但不是所有角度),则正方形可能会变成矩形或平行四边形。例如,当从倾斜角度观看远处的广告牌时,或者当平面物体的阴影落在与其不平行的表面上时,就会发生这种情况。
当比例因子大于 1 时,(均匀或非均匀)缩放有时也称为膨胀(dilation)或放大(enlargement)。当比例因子为小于 1 的正数时,缩放有时也称为收缩(contraction)或缩减(reduction)。
在最一般的意义上,缩放包括缩放方向不垂直的情况。它还包括一个或多个比例因子等于零的情况(投影),以及一个或多个负比例因子的情况(-1 的方向缩放等同于反射)。
缩放是一种线性变换,是位似变换(homothetic transformation)的特例(关于一个点缩放)。在大多数情况下,位似变换是非线性变换。
2.1 均匀缩放(Uniform scaling)
比例因子通常是一个小数,它可以缩放或乘以某个数量。在等式 y = C x y = Cx y=Cx 中, C C C 是 x x x 的比例因子。 C C C 也是 x x x 的系数,可称为 y y y 对 x x x 的比例常数。例如,加倍距离对应于距离的比例因子 2,而将蛋糕切成两半会导致块的体积比例因子为二分之一。它的基本方程是像除以原像。
在测量领域,仪器的比例因子有时被称为灵敏度(sensitivity)。两个相似几何图形中任意两个对应长度的比值也称为比例(scale)。
2.2 矩阵表示
缩放可以由缩放矩阵表示(scaling matrix)。要通过向量 v = ( v x , v y , v z ) v = (v_{x}, v_{y}, v_{z}) v=(vx,vy,vz) 缩放对象,每个点 p = ( p x , p y , p z ) p = (p_{x}, p_{y}, p_{z}) p=(px,py,pz) 都需要与此缩放矩阵相乘:
S v = [ v x 0 0 0 v y 0 0 0 v z ] S_{v}={\begin{bmatrix}v_{x}&0&0\\0&v_{y}&0\\0&0&v_{z}\\\end{bmatrix}} Sv= vx000vy000vz
如下所示,乘法将给出预期的结果:
S v p = [ v x 0 0 0 v y 0 0 0 v z ] [ p x p y p z ] = [ v x p x v y p y v z p z ] S_{v}p={\begin{bmatrix}v_{x}&0&0\\0&v_{y}&0\\0&0&v_{z}\\\end{bmatrix}}{\begin{bmatrix}p_{x}\\ p_{y}\\p_{z}\end{bmatrix}}={\begin{bmatrix}v_{x}p_{x}\\v_{y}p_{y}\\v_{z}p_{z }\end{bmatrix}} Svp= vx000vy000vz pxpypz = vxpxvypyvzpz
这种缩放将物体的直径改变为比例因子之间的一个因子,面积改变为两个比例因子的最小和最大乘积之间的一个因子,体积为所有三个的乘积。
当且仅当缩放因子相等( v x = v y = v z v_{x} = v_{y} = v_{z} vx=vy=vz)时,缩放是均匀的。如果除比例因子之一以外的所有比例因子都等于 1,则我们有方向缩放。
在 v x = v y = v z = k v_{x} = v_{y} = v_{z} = k vx=vy=vz=k 的情况下,缩放将任何表面的面积增加 k 2 k^{2} k2 倍,将任何固体物体的体积增加 k 3 k^{3} k3 倍。
2.2.1 任意维度缩放
在 n n n 维空间 R n \mathbb {R} ^{n} Rn,均匀缩放一个因子 v v v 通过标量乘法完成,即每个点的每个坐标乘以 v v v。作为线性变换的特例,也可以通过将每个点(视为列向量)乘以对角矩阵,其对角线上的元素都等于 v v v,即 v I vI vI。
非均匀缩放是通过与任何对称矩阵相乘来实现的。矩阵的特征值是比例因子,相应的特征向量是每个比例因子应用的轴。一种特殊情况是对角矩阵,具有任意数字 v 1 , v 2 , … v n v_{1},v_{2},\ldots v_{n} v1,v2,…vn 沿对角线:缩放轴则为坐标轴,变换 通过因子 v i v_{i} vi 沿各轴 i i i 缩放。
在使用非零比例因子的均匀缩放中,所有非零向量都保持它们的方向(从原点看),或者所有的方向都反转,这取决于比例因子的符号。在非均匀缩放中,只有属于特征空间的向量会保持其方向。属于不同特征空间的两个或多个非零向量之和的向量将向具有最大特征值的特征空间倾斜。
2.3 使用齐次坐标
在计算机图形学经常使用的射影几何中,点使用齐次坐标(homogeneous coordinates)表示。要通过向量 v = ( v x , v y , v z ) v = (v_{x}, v_{y}, v_{z}) v=(vx,vy,vz) 缩放对象,每个齐次坐标向量 p = ( p x , p y , p z , 1 ) p = (p_{x}, p_{y}, p_{z}, 1) p=(px,py,pz,1) 需要与此投影变换(projective transformation)矩阵相乘:
S v = [ v x 0 0 0 0 v y 0 0 0 0 v z 0 0 0 0 1 ] S_{v}={\begin{bmatrix}v_{x}&0&0&0\\0&v_{y}&0&0\\0&0&v_{z}&0\\0&0&0&1\end{bmatrix}} Sv= vx0000vy0000vz00001
如下所示,乘法将给出预期的结果:
S v p = [ v x 0 0 0 0 v y 0 0 0 0 v z 0 0 0 0 1 ] [ p x p y p z 1 ] = [ v x p x v y p y v z p z 1 ] S_{v}p={\begin{bmatrix}v_{x}&0&0&0\\0&v_{y}&0&0\\0&0&v_{z}&0\\0&0&0&1\end{bmatrix}}{\begin{bmatrix}p_{x} \\p_{y}\\p_{z}\\1\end{bmatrix}}={\begin{bmatrix}v_{x}p_{x}\\v_{y}p_{y}\\v_{ z}p_{z}\\1\end{bmatrix}} Svp= vx0000vy0000vz00001 pxpypz1 = vxpxvypyvzpz1
由于齐次坐标的最后一个分量可以看作是其他三个分量的分母,因此可以通过使用此缩放矩阵来完成公因子 s s s 的均匀缩放:
S v = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 s ] S_{v}={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&{\frac {1}{s}}\end{bmatrix}} Sv= 100001000010000s1
对于每个向量 p = ( p x , p y , p z , 1 ) p = (p_{x}, p_{y}, p_{z}, 1) p=(px,py,pz,1) 我们会有:
S v p = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 s ] [ p x p y p z 1 ] = [ p x p y p z 1 s ] {\displaystyle S_{v}p={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&{\frac {1}{s}}\end{bmatrix}}{\begin{bmatrix}p_{x }\\p_{y}\\p_{z}\\1\end{bmatrix}}={\begin{bmatrix}p_{x}\\p_{y}\\p_{z}\\{\frac {1}{s}}\end{bmatrix}}} Svp= 100001000010000s1 pxpypz1 = pxpypzs1
这相当于
[ s p x s p y s p z 1 ] {\begin{bmatrix}sp_{x}\\sp_{y}\\sp_{z}\\1\end{bmatrix}} spxspyspz1
2.4 函数扩张(dilation)和收缩(contraction)
给定一点 P ( x , y ) P(x,y) P(x,y),膨胀通过下面方程,将它与点 P ′ ( x ′ , y ′ ) P'(x',y') P′(x′,y′) 相关联:
{ x ′ = m x y ′ = n y for m , n ∈ R + {\displaystyle {\begin{cases}x'=mx\\y'=ny\end{cases}}} \ \ \text{for}\ \ {\displaystyle m,n\in \mathbb {R} ^{+}} {x′=mxy′=ny for m,n∈R+
因此,给定一个函数 y = f ( x ) y=f(x) y=f(x),扩张函数(dilated function)的方程为:
y = n f ( x m ) {\displaystyle y=nf\left({\frac {x}{m}}\right)} y=nf(mx)
2.4.1 特殊情况
如果 n = 1 n=1 n=1,变换是水平的(horizontal);当 m > 1 m>1 m>1,是膨胀,当 m < 1 m<1 m<1,它是一个收缩。
如果 m = 1 m=1 m=1,变换是垂直的(vertical);当 n > 1 n>1 n>1,是膨胀,当 n < 1 n<1 n<1,是收缩。
如果 m = 1 / n m=1/n m=1/n 或 n = 1 / m n=1/m n=1/m,变换是挤压映射(squeeze mapping)。
3. 标度不变性
图 Wiener process 是标度不变的
在物理学、数学和统计学中,标度不变性(或尺度不变性)是物体或定律的一个特征,如果长度、能量或其他变量的尺度乘以一个公因数,这些物体或定律不会改变,因此代表了一种普适性。
这种变换的技术术语是扩张(dilatation or dilation)。扩张可以形成更大的共形对称性(conformal symmetry)的一部分。
- 在数学中,标度不变性通常是指单个函数或曲线的不变性。 一个密切相关的概念是自相似性,其中函数或曲线在扩张的离散子集下是不变的。随机过程的概率分布也有可能表现出这种标度不变性或自相似性。
- 在经典场论中,标度不变性最常用于整个理论在膨胀下的不变性。这些理论通常描述没有特征长度尺度的经典物理过程。
- 在量子场论中,标度不变性有粒子物理学的解释。在标度不变理论中,粒子相互作用的强度不取决于所涉及粒子的能量。
- 在统计力学中,标度不变性是相变的一个特征。关键的观察是,在相变或临界点附近,所有长度尺度都会发生涨落,因此应该寻找一种明确的标度不变理论来描述这种现象。这种理论是标度不变的统计场论(statistical field theories),在形式上与标度不变的量子场论非常相似。
- 普适性(universality)是指观察到广泛不同的微观系统可以在相变时表现出相同的行为。因此,许多不同系统中的相变可以用相同的基础标度不变理论来描述。
- 通常,无量纲量(dimensionless quantities)是标度不变的。统计学中类似的概念是标准化矩(standardized moments),它是变量的标度不变统计,而非标准化矩(unstandardized moments)则不是。
3.1 标度不变(Scale-invariant)曲线和自相似性(self-similarity)
在数学中,可以考虑函数或曲线 f ( x ) f (x) f(x) 在变量 x x x 重新缩放下的缩放属性。也就是说,人们对某个比例因子 λ \lambda λ 下的 f ( λ x ) f (\lambda x) f(λx) 的形状感兴趣,可以将其视为长度或大小重新缩放。 f ( x ) f(x) f(x) 在所有重新缩放下都不变的要求通常被认为是:
f ( λ x ) = λ Δ f ( x ) f(\lambda x)=\lambda ^{\Delta }f(x) f(λx)=λΔf(x)
其中指数 Δ \Delta Δ 与函数 f ( x ) f(x) f(x) 有关,缩放的系数 λ \lambda λ 是任意的(除了后续的分形外),这相当于 f f f 是次数为 Δ \Delta Δ 的齐次函数。
标度不变函数的例子是单项式 f ( x ) = x n f(x)=x^{n} f(x)=xn, 其中 Δ = n \Delta = n Δ=n,很明显:
f ( λ x ) = ( λ x ) n = λ n f ( x ) f(\lambda x)=(\lambda x)^{n}=\lambda ^{n}f(x) f(λx)=(λx)n=λnf(x)
标度不变曲线的一个例子是对数螺线,这是自然界中经常出现的一种曲线。在极坐标 ( r , θ ) (r, \theta) (r,θ) 中,螺旋可以写为:
θ = 1 b ln ( r / a ) \theta ={\frac {1}{b}}\ln(r/a) θ=b1ln(r/a)
考虑到曲线的旋转,它在所有重新缩放 λ \lambda λ 下都是不变的;也就是说, θ ( λ r ) \theta(\lambda r) θ(λr) 与 θ ( r ) \theta(r) θ(r) 的旋转形式相同。
3.1.1 射影几何
单项式的标度不变性的思想在更高维度上推广到齐次多项式的思想,更一般地推广到齐次函数。齐次函数是射影空间(projective space)的自然存在,齐次多项式在射影几何(projective geometry)中作为射影变体(projective varieties)进行研究。射影几何是一个特别丰富的数学领域。在其最抽象的形式中,格式(schemeshttps://en.wikipedia.org/wiki/Scheme_(mathematics))的几何,它与弦理论中的各种主题都有联系。
3.1.2 分形
有时说分形是标度不变的,但更准确地说,应该说它们是自相似的。分形通常仅对于一组离散值 λ \lambda λ 等于自身,即使这样,也可能必须应用平移和旋转以使分形与自身匹配。
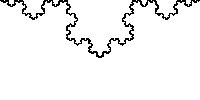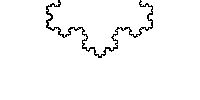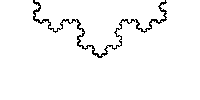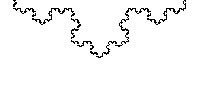
图 自相似的 Koch curve
因此,例如,Koch curve 随 Δ = 1 \Delta = 1 Δ=1 缩放,但缩放仅适用于 n n n 为整数时, λ = 1 3 n \lambda = \frac{1}{3}^{n} λ=31n 值。此外,Koch curve 不仅在原点缩放,而且在某种意义上“无处不在”:沿着曲线可以找到它自己的微型副本。
注意在研究 Koch curve 的自相似中,横坐标和纵坐标都需要放大,两者放大的倍数不同也会影响最终的相似性,在 Koch curve 中横纵坐标都是按照相同倍数(离散的)放大,此时呈现严格的自相似性,以为每个被放大的细节都可充当原始图像的精确副本。但在其他函数曲线中,可能需要横纵坐标放大倍数不同,才能直观看到曲线的自相似性。比如函数曲线 f ( x ) = x 2 f(x)=x^{2} f(x)=x2 中,如果将函数缩放 λ \lambda λ,则 f ( λ x ) = λ 2 x 2 f(\lambda x)=\lambda^{2}x^{2} f(λx)=λ2x2,即横坐标缩放 λ \lambda λ 的时候,纵坐标需要缩放 λ 2 \lambda^{2} λ2,才能保持曲线在缩放的过程中保持不变(自相似),否则曲线就会变形。
注意上述有关自相似的缩放操作,本质上是基于朴实的视觉感受得到的,从这种朴实的视觉角度出发,会更好的理解自相似概念。
一些分形可能同时具有多个比例因子;这种缩放是通过多重分形分析(multi-fractal analysis)研究的。
周期性的外部和内部射线(external and internal rays)是不变曲线。
3.2 随机过程中的标度不变性
如果 P ( f ) P(f) P(f) 是频率 f f f 下的平均期望功率,则噪声按比例缩放:
P ( f ) = λ − Δ P ( λ f ) P(f)=\lambda ^{-\Delta }P(\lambda f) P(f)=λ−ΔP(λf)
Δ = 0 \Delta = 0 Δ=0 表示白噪声, Δ = − 1 \Delta = −1 Δ=−1 表示粉红噪声, Δ = − 2 \Delta = −2 Δ=−2 表示布朗噪声(更一般地说,布朗运动)。之所以这样定义,是因为上述几种噪声形式都是幂指数的(或单项式)。
更准确地说,随机系统中的缩放涉及从所有可能的随机构型集(random configurations)中选择特定构型的可能性。这种可能性由概率分布给出。
标度不变分布的示例是 Pareto distribution 和 Zipfian distribution。
3.2.1 标度不变的 Tweedie distribution
Tweedie distribution 是指数分散模型(exponential dispersion models)的一个特例,它是一类统计模型,用于描述广义线性模型(generalized linear model)的误差分布(error distributions),其特点是在加法和再生卷积(reproductive convolution)以及标度变换下具有闭合性。其中包括许多常见的分布:正态分布、泊松分布和伽马分布,以及更不寻常的分布,如 compound Poisson-gamma distribution、positive stable distributions 和 extreme stable distributions。由于其固有的标度不变性,Tweedie 随机变量 Y Y Y 给出方差 var ( Y ) \text{var}(Y) var(Y) 与 E ( Y ) \text{E}(Y) E(Y) 之间的幂律关系:
var ( Y ) = a [ E ( Y ) ] p {\text{var}}\,(Y)=a[{\text{E}}\,(Y)]^{p} var(Y)=a[E(Y)]p
其中 a a a 和 p p p 是正常数。这种方差与均值之间的幂律关系,在物理学文献中称为涨落标度(fluctuation scaling),在生态学文献中称为 Taylor’s law。
由 Tweedie 分布支配并通过扩展格子的方法(https://en.wikipedia.org/wiki/Tweedie_distributions)评估的随机序列,在方差与均值幂律和幂律自相关之间表现出双条件关系(biconditional relationship)Wiener-Khinchin 定理进一步暗示,对于在这些条件下表现出均值幂律方差的任何序列,也将表现出 1 / f 1/f 1/f 噪声。
Tweedie 收敛定理(Tweedie convergence theorem)为涨落标度(fluctuation scaling)和 1 / f 1/f 1/f 噪声的广泛出现提供了假设性解释。从本质上讲,它要求任何渐近地表明均值幂律方差的指数分散模型(exponential dispersion model)都需要表现为一个方差函数,该方差函数(variance function)位于 Tweedie 模型的吸引力域内。几乎所有具有有限累积生成函数(finite cumulant generating functions)的分布函数都符合指数分散模型(exponential dispersion models)的条件,并且大多数指数分散模型都表现出这种形式的方差函数。因此,许多概率分布具有表示这种渐近行为(asymptotic behavior)的方差函数,并且 Tweedie 分布成为各种数据类型的收敛焦点。
就像中心极限定理要求某些类型的随机变量具有作为收敛焦点的高斯分布并表现为白噪声一样,Tweedie 收敛定理要求某些非高斯随机变量表达 1 / f 1/f 1/f 噪声和涨落标度。
3.2.2 宇宙学
在物理宇宙学中,宇宙微波背景(cosmic microwave background)空间分布的功率谱接近标度不变函数。虽然在数学中这意味着频谱是幂律,但在宇宙学中术语“标度不变”表示作为波数 k k k 函数的原始涨落的振幅 P ( k ) P(k) P(k) 近似恒定,即平坦的频谱。这种模式与宇宙膨胀的提议是一致的。
3.3 经典场论中的标度不变性
经典场论通常由依赖于坐标 x x x 下的一个场或场 φ \varphi φ 的集合来描述。然后通过求解 φ \varphi φ 的微分方程来确定有效的场构型,这些方程称为场方程(field equations)。
对于一个标度不变的理论,结合一些指定的场重新缩放,它的场方程在坐标的重新缩放下应该是不变的:
x → λ x φ → λ − Δ φ x\rightarrow \lambda x\\ \varphi \rightarrow \lambda ^{-\Delta }\varphi x→λxφ→λ−Δφ
参数 Δ \Delta Δ 被称为场的标度维度(scaling dimension),其值取决于所考虑的理论。如果理论中没有出现固定长度尺度(fixed length scale),标度不变性通常会成立。相反,固定长度尺度的存在表明理论不是标度不变的。
标度不变的结果是,给定一个标度不变场方程的解,我们可以通过适当地重新缩放坐标和场来自动找到其他解。更具体的,给定一个解 φ ( x ) \varphi(x) φ(x),总是有其他形式的解:
λ Δ φ ( λ x ) \lambda ^{\Delta }\varphi (\lambda x) λΔφ(λx)
3.3.1 场构型(field configurations)的标度不变性
对于特定的场构型 φ ( x ) \varphi(x) φ(x),要保持标度不变,我们要求:
φ ( x ) = λ − Δ φ ( λ x ) \varphi (x)=\lambda ^{-\Delta }\varphi (\lambda x) φ(x)=λ−Δφ(λx)
其中 Δ \Delta Δ 是场的标度维度。
我们注意到这个条件是相当严格的。一般来说,即使是标度不变场方程的解也不是标度不变的,在这种情况下,对称性被称为自发破缺(spontaneously broken)。
3.3.2 经典电磁学
标度不变的经典场论的一个例子是没有电荷或电流的电磁学。这些场是电场和磁场, E ( x , t ) \mathbf{E}(\mathbf{x},t) E(x,t) 和 B ( x , t ) \mathbf{B}(\mathbf{x},t) B(x,t),而它们的场方程是麦克斯韦方程。
在没有电荷或电流的情况下,这些场方程采用波动方程的形式
∇ 2 E = 1 c 2 ∂ 2 E ∂ t 2 ∇ 2 B = 1 c 2 ∂ 2 B ∂ t 2 \nabla ^{2}\mathbf {E} ={\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2} }}\\ \nabla ^{2}\mathbf {B} ={\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {B} }{\partial t^{2} }} ∇2E=c21∂t2∂2E∇2B=c21∂t2∂2B
其中 c c c 是光速。
这些场方程在变换下不变:
x → λ x t → λ t x\rightarrow\lambda x\\ t\rightarrow\lambda t x→λxt→λt
此外,给定麦克斯韦方程组的解 E ( x , t ) \mathbf{E}(\mathbf{x}, t) E(x,t) 和 B ( x , t ) \mathbf{B}(\mathbf{x}, t) B(x,t),则 E ( λ x , λ t ) \mathbf{E}(\lambda\mathbf{x}, \lambda t) E(λx,λt) 和 B ( λ x , λ t ) \mathbf{B}(\lambda\mathbf{x}, \lambda t) B(λx,λt) 也是解。
3.3.3 无质量标量场论(Massless scalar field theory)
标度不变经典场论的另一个例子是无质量标量场(请注意,名称标量(scalar)与标度(scale)不变性无关)。标量场 φ ( x , t ) \varphi(x, t) φ(x,t) 是一组空间变量 x x x 和时间变量 t t t 的函数。
首先考虑线性理论。和上面的电磁场方程一样,这个理论的运动方程也是一个波动方程,
1 c 2 ∂ 2 φ ∂ t 2 − ∇ 2 φ = 0 {\frac {1}{c^{2}}}{\frac {\partial ^{2}\varphi }{\partial t^{2}}}-\nabla ^{2}\varphi =0 c21∂t2∂2φ−∇2φ=0
并且在变换下不变
x → λ x t → λ t x\rightarrow\lambda x\\ t\rightarrow\lambda t x→λxt→λt
无质量这个名字是指在场方程中没有 ∝ m 2 φ \propto m^{2}\varphi ∝m2φ 这一项。这一项通常被称为“质量”项,并且会破坏上述变换下的不变性。在相对论场论中,质量标度(mass-scale) m m m 在物理上等同于固定长度的标度,通过:
L = ℏ m c L={\frac {\hbar }{mc}} L=mcℏ
因此,大质量标量场论不是标度不变的也就不足为奇了。
3.3.4 φ 4 \varphi^{4} φ4 理论
上面示例中的场方程在场中都是线性的,这意味着标度维度 Δ \Delta Δ 并不那么重要。然而,通常要求标量场作用是无量纲的,这就固定了 φ \varphi φ 的标度维数。 尤其是,
Δ = D − 2 2 \Delta ={\frac {D-2}{2}} Δ=2D−2
其中 D D D 是空间和时间维度的组合数。
给定 φ \varphi φ 的这个标度维数,无质量标量场论的某些非线性修改也是标度不变的。一个例子是 D = 4 D=4 D=4 的无质量 φ 4 \varphi^{4} φ4 理论。场方程为:
1 c 2 ∂ 2 φ ∂ t 2 − ∇ 2 φ + g φ 3 = 0 {\frac {1}{c^{2}}}{\frac {\partial ^{2}\varphi }{\partial t^{2}}}-\nabla ^{2}\varphi +g\varphi ^{3}=0 c21∂t2∂2φ−∇2φ+gφ3=0
(请注意,名称 φ 4 \varphi^{4} φ4 源自拉格朗日量的形式,其中包含 φ \varphi φ 的四次方。)
当 D = 4 D=4 D=4 时(例如三个空间维度和一个时间维度),标量场标度维度为 Δ = 1 \Delta=1 Δ=1。然后场方程在变换下不变:
x → λ x t → λ t φ ( x ) → λ − 1 φ ( x ) x\rightarrow\lambda x\\ t\rightarrow\lambda t\\ \varphi (x)\rightarrow \lambda ^{-1}\varphi (x) x→λxt→λtφ(x)→λ−1φ(x)
关键是参数 g g g 必须是无量纲的,否则就会在理论中引入定长尺度:对于 φ 4 \varphi^{4} φ4 理论,这只是 D = 4 D=4 D=4 的情况。请注意,在这些转换下,函数 φ \varphi φ 的参数没有改变。
3.4 量子场论中的标度不变性
量子场论(quantum field theory,QFT)的尺度依赖性(scale-dependence)的特征在于其耦合参数(coupling parameters)取决于给定物理过程的能量尺度(energy-scale)的方式。这种能量依赖性由重整化群描述,并编码在理论的 beta-functions 中。
对于标度不变的 QFT,其耦合参数必须独立于能量尺度,这由理论的 beta-functions 的消失表明。此类理论也称为相应重整化群流的不动点(fixed points of the corresponding renormalization group flow)。
3.4.1 量子电动力学
标度不变 QFT 的一个简单示例是没有带电粒子的量子化电磁场。该理论实际上没有耦合参数(因为光子无质量且无相互作用),因此是标度不变的,很像经典理论。
然而,在自然界中,电磁场耦合到带电粒子,例如电子。描述光子和带电粒子相互作用的 QFT 是量子电动力学(QED),该理论不是标度不变的。我们可以从 QED beta-functions 中看出这一点。这告诉我们电荷(理论上是耦合参数)随着能量的增加而增加。因此,虽然没有带电粒子的量子化电磁场是标度不变的,但 QED 不是标度不变的。
3.4.2 无质量标量场论
自由、无质量的量子化标量场论(quantized scalar field theory)没有耦合参数。因此,与经典版本一样,它是标度不变的。在重整化群的语言中,这个理论被称为高斯不动点(Gaussian fixed point)。
然而,即使经典无质量 φ 4 \varphi^{4} φ4 理论在 D = 4 D=4 D=4 时是标度不变的,但量子化版本(quantized version)不是标度不变的。 我们可以从耦合参数 g g g 的 beta-functions 中看出这一点。
尽管量子化的无质量 φ 4 \varphi^{4} φ4 不是标度不变的,但除了高斯不动点之外,确实存在标度不变的量子化标量场理论。一个例子是下面的 Wilson–Fisher fixed point。
3.4.3 共形场论(Conformal field theory)
标度不变 QFT 在完全共形对称(conformal symmetry)下几乎总是不变的,研究此类 QFT 的是共形场论(conformal field theory,CFT)。CFT 中的运算符具有明确定义的标度维度,类似于上面讨论的经典场的标度维度 Δ \Delta Δ。然而,CFT 中算子的标度维度通常不同于相应经典理论中的场。CFT 中出现的额外贡献被称为异常标度维度(anomalous scaling dimensions)。
3.4.4 标度和共形异常(Scale and conformal anomalies)
上面的 φ 4 \varphi^{4} φ4 理论示例表明,即使相应的经典场论是标度不变(或共形不变),量子场论的耦合参数也可以是标度相关的(scale-dependent)。如果是这种情况,则称经典标度(或共形)不变性是反常的(anomalous)。一个经典的标度不变场论,其中标度不变性被量子效应打破,提供了对早期宇宙近乎指数膨胀的解释,称为宇宙膨胀,只要该理论可以通过微扰理论进行研究。
3.5 相变
在统计力学中,当系统经历相变时,其涨落由标度不变统计场论描述(statistical field theory)。对于在 D D D 空间维度上处于平衡状态(即与时间无关)的系统,相应的统计场论在形式上类似于 D D D 维 CFT。此类问题中的标度维度通常称为临界指数,原则上可以在适当的 CFT 中计算这些指数。
3.5.1 伊辛模型
将本文中的许多想法联系在一起的一个例子是 Ising 模型的相变,这是铁磁物质的一个简单模型。这是一个统计力学模型,也有共形场论的描述。该系统由一组晶格点组成,这些点阵形成一个 D D D 维周期性晶格。与每个晶格位置相关联的是磁矩或自旋,该自旋可以取值 +1 或 -1。(这些状态也分别称为向上和向下。)
关键是伊辛模型具有自旋-自旋相互作用,这使得它在能量上有利于两个相邻的自旋对齐。另一方面,热波动通常会在自旋排列中引入随机性。在某个临界温度 T c T_{\mathrm{c}} Tc 下,据说会发生自发磁化。这意味着在 T c T_{\mathrm{c}} Tc 以下,自旋-自旋相互作用将开始占主导地位,并且在两个方向之一上存在一些自旋净排列。
在这个临界温度下,人们想要计算的物理量类型的一个例子是相隔距离 r r r 的自旋之间的相关性。这具有一般行为:
G ( r ) ∝ 1 r D − 2 + η G(r)\propto {\frac {1}{r^{D-2+\eta }}} G(r)∝rD−2+η1
对于某些特定值 η \eta η ,这是一个临界指数的例子。
3.5.1.1 CFT 描述
温度 T c T_{\mathrm{c}} Tc 的涨落是尺度不变的,因此这个相变的伊辛模型有望用标度不变的统计场论来描述。事实上,这个理论就是 Wilson–Fisher fixed point,一种特殊的标度不变标量场理论。
在这种情况下, G ( r ) G(r) G(r) 被理解为标量场的相关函数,
⟨ ϕ ( 0 ) ϕ ( r ) ⟩ ∝ 1 r D − 2 + η \langle \phi (0)\phi (r)\rangle \propto {\frac {1}{r^{D-2+\eta }}} ⟨ϕ(0)ϕ(r)⟩∝rD−2+η1
现在我们可以将已经看到的一些想法组合在一起。
从上面可以看出,该相变的临界指数 η \eta η 也是一个反常维度(anomalous dimension)。这是因为标量场的经典维度,
Δ = D − 2 2 \Delta ={\frac {D-2}{2}} Δ=2D−2
修改为
Δ = D − 2 + η 2 \Delta ={\frac {D-2+\eta }{2}} Δ=2D−2+η
其中 D D D 是伊辛模型晶格的维数。
因此,共形场论中的这个反常维数与伊辛模型相变的特定临界指数相同。
请注意,对于维度 D ≡ 4 − ε D \equiv 4−\varepsilon D≡4−ε,可以使用 epsilon expansion 近似计算 η \eta η,并且发现:
η = ε 2 54 + O ( ε 3 ) \eta ={\frac {\varepsilon ^{2}}{54}}+O(\varepsilon ^{3}) η=54ε2+O(ε3)
在物理上有趣的三个空间维度的情况下,我们有 ε = 1 \varepsilon=1 ε=1,因此这种展开并不严格可靠。然而,半定量预测是 η \eta η 在三个维度上数值较小。
另一方面,在二维情况下,伊辛模型是完全可解的。特别是,它等同于最小模型之一,即一系列广为人知的 CFT,并且可以精确计算 η \eta η(和其他临界指数),
η D = 2 = 1 4 。 \eta _{_{D=2}}={\frac {1}{4}}。 ηD=2=41。
3.5.2 Schramm–Loewner evolution
某些二维 CFT 中的异常维度可能与随机游动的典型分形维数有关,其中随机游动是通过 Schramm–Loewner evolution(SLE)定义的。正如我们在上面看到的,CFT 描述了相变的物理学,因此可以将某些相变的临界指数与这些分形维数联系起来。示例包括 2 d 2d 2d 临界 Ising 模型和更一般的 2 d 2d 2d 临界 Potts model。将其他 2 d 2d 2d CFT 与 SLE 相关联是一个活跃的研究领域。
3.6 标度不变性的其他例子
3.6.1 无外作用力的牛顿流体力学
在某些情况下,流体力学是标度不变的经典场论。这些场是流体流动的速度, u ( x , t ) \mathbf {u} (\mathbf {x} ,t) u(x,t),流体密度, ρ ( x , t ) \rho (\mathbf {x} ,t) ρ(x,t),以及流体压力, P ( x , t ) P(\mathbf {x} ,t) P(x,t)。这些场必须同时满足 Navier-Stokes 方程和连续性方程。对于牛顿流体,它们采用各自的形式:
ρ ∂ u ∂ t + ρ u ⋅ ∇ u = − ∇ P + μ ( ∇ 2 u + 1 3 ∇ ( ∇ ⋅ u ) ) ∂ ρ ∂ t + ∇ ⋅ ( ρ u ) = 0 \begin{aligned} &\rho {\frac {\partial \mathbf {u} }{\partial t}}+\rho \mathbf {u} \cdot \nabla \mathbf {u} =-\nabla P+\mu \left( \nabla ^{2}\mathbf {u} +{\frac {1}{3}}\nabla \left(\nabla \cdot \mathbf {u} \right)\right)\\ &\frac {\partial \rho }{\partial t}+\nabla \cdot \left(\rho \mathbf {u} \right)=0 \end{aligned} ρ∂t∂u+ρu⋅∇u=−∇P+μ(∇2u+31∇(∇⋅u))∂t∂ρ+∇⋅(ρu)=0
其中 μ \mu μ 是动力粘度(dynamic viscosity)。
为了推导出这些方程的标度不变性,我们指定了一个状态方程,将流体压力与流体密度相关联。状态方程取决于流体的类型及其所处的条件。例如,我们考虑等温理想气体,它满足:
P = c s 2 ρ P=c_{s}^{2}\rho P=cs2ρ
其中 c s c_{s} cs 是流体中的声速。鉴于此状态方程,Navier-Stokes 和连续性方程在变换下不变:
x → λ x t → λ 2 t ρ → λ − 1 ρ u → λ − 1 u \begin{aligned} x&\rightarrow\lambda x\\ t&\rightarrow \lambda ^{2}t\\ \rho &\rightarrow \lambda ^{-1}\rho\\ \mathbf {u} &\rightarrow \lambda ^{-1}\mathbf {u} \end{aligned} xtρu→λx→λ2t→λ−1ρ→λ−1u
给定解 u ( x , t ) \mathbf {u} (\mathbf {x} ,t) u(x,t) 和 ρ ( x , t ) \rho (\mathbf {x} ,t) ρ(x,t),我们自动得到 λ u ( λ x , λ 2 t ) \lambda \mathbf {u} (\lambda \mathbf {x} ,\lambda ^{2}t) λu(λx,λ2t) 和 λ ρ ( λ x , λ 2 t ) \lambda \rho (\lambda \mathbf {x} ,\lambda ^{2}t) λρ(λx,λ2t) 也是解。
3.6.2 液体和固体中隐藏的标度不变性
分子动力学计算机模拟研究的某些模型,包括 Lennard-Jones 和 Yukawa pair-potential models,具有势能函数 U ( R ) U(\mathbf {R} ) U(R) 一个很好的近似值遵循“隐藏标度不变性”标准:
U ( R a ) < U ( R b ) ⇒ U ( λ R a ) < U ( λ R b ) {\displaystyle U(\mathbf {R} _{\rm {a}})<U(\mathbf {R} _{\rm {b}})\,\Rightarrow \,U(\lambda \mathbf {R } _{\rm {a}})<U(\lambda \mathbf {R} _{\rm {b}})} U(Ra)<U(Rb)⇒U(λRa)<U(λRb)
这里 R a \mathbf {R} _{\rm {a}} Ra 和 R b \mathbf {R} _{\rm {b}} Rb 是两个相同密度构型的完整空间坐标, λ \lambda λ 是一个将构型统一缩放到不同密度的参数。隐藏标度不变性意味着如果将这些排列均匀地缩放到不同的密度,则根据它们的势能保持一个密度的构型排序。这仅严格适用于具有欧拉齐次势能函数的系统,例如,粒子与逆幂律对势相互作用(inverse-power-law pair potentials)的系统。当隐藏标度不变性意味着大多数构型时,这意味着热力学相图中存在线,即所谓的“同构”,沿着这些线,简化单元中的结构和动力学对于一个好的近似是不变的。据信,大多数金属和范德瓦尔斯键合系统在液相和固相中都遵循这种近似对称性,而具有强方向键的系统(如共价键或氢键系统)则不然;离子和偶极系统构成介于两者之间的一类。大多数系统在气相中不服从隐藏的标度不变性。由于同构(isomorph)是恒定超熵线(line of constant excess entropy),同构的存在在很大程度上解释了 Rosenfeld 于 1977 年发现的超熵标度(excess-entropy scaling),以及为什么这也适用于混合物、受限系统、分子系统等。
3.6.3 计算机视觉
在计算机视觉和生物视觉中,由于透视图像映射和世界上具有不同物理尺寸的物体,会出现缩放变换。在这些领域中,标度不变性是指当图像域中的局部尺度发生变化时,图像数据的局部图像描述符或视觉表示保持不变。在标准化导数响应(normalized derivative responses)的尺度上检测局部最大值为从图像数据中获得标度不变性提供了一个通用框架。应用示例包括通过标度不变特征变换(scale-invariant feature transform)进行的斑点检测(blob detection)、角点检测(corner detection)、脊线检测(ridge detection)和目标识别(object recognition)。
3.7 标度空间(Scale space)
3.8 标度不变特征变换(Scale-invariant feature transform)
wiki: Scale-invariant feature transform
3.9 普适性(Universality)
在统计力学中,普适性是指观察到一大类系统的属性独立于系统的动态细节。当大量相互作用的部分聚集在一起时,系统在缩放限制中显示出普适性。该术语的现代含义由 Leo Kadanoff 在 1960 年代引入,但该概念的更简单版本已经隐含在范德瓦尔斯方程和较早的朗道相变理论中,后者没有正确地包含缩放。
这个术语在数学的几个领域中逐渐得到更广泛的使用,包括组合学和概率论,只要结构的定量特征(例如渐近行为)可以从定义中出现的几个全局参数推导出来,而不需要了解系统的细节。
重整化群(renormalization group)提供了一种直观的、吸引人的、尽管在数学上并不严格的普适性解释。它将统计场论中的算子分为相关和不相关。相关算子负责扰动自由能,虚时间拉格朗日,这将影响连续极限,并且可以在远距离看到。不相关的算子是那些只改变短距离细节的算子。标度不变统计理论的集合定义了普适类(universality classes),相关算子的有限维系数列表参数化了近临界行为(near-critical behavior)。
3.9.1 统计力学中的普适性
普适性的概念起源于统计力学中相变的研究。当材料以急剧的方式改变其特性时,就会发生相变:水在加热时沸腾并变成蒸汽;或磁铁在加热时会失去磁性。相变的特征在于有序参数,例如密度或磁化强度,其作为系统参数(例如温度)的函数而变化。系统改变其所在相的参数的特殊值是系统的临界点(critical value)。对于表现出普适性的系统,参数越接近其临界值,序参量对系统细节的依赖就越不敏感。
如果参数 β \beta β 在值 β c \beta_{\mathrm{c}} βc 处是临界的,那么序参量 a a a 将很好地近似为:
a = a 0 ∣ β − β c ∣ α {\displaystyle a=a_{0}\left\vert \beta -\beta _{c}\right\vert ^{\alpha }} a=a0∣β−βc∣α
指数 α \alpha α 是系统的临界指数(critical exponent)。二十世纪下半叶的一项非凡发现是,非常不同的系统具有相同的临界指数。
1975 年,Mitchell Feigenbaum 发现了迭代映射的普适性。
3.9.2 例子
普适性之所以得名,是因为它出现在各种各样的物理系统中。普适性的例子包括:
- 成堆的沙子崩塌。雪崩的可能性与雪崩的大小成幂律比例,并且可以看到雪崩发生在所有大小的尺度上。这被称为“自组织临界性(self-organized criticality)”。
- 从钢铁到岩石再到纸张,各种材料中裂纹和撕裂的形成和传播。撕裂方向的变化,或断口表面的粗糙度,与尺寸比例成幂律比例。
- 电介质的电击穿,类似于裂缝和撕裂。
- 流体通过无序介质的逾渗,例如石油通过破裂的岩床,或水通过滤纸,例如在色谱法中。幂律标度将流速与裂缝分布联系起来。
- 分子在溶液中的扩散,以及扩散限制聚集(diffusion-limited aggregation)现象。
- 不同大小的岩石在被摇动的颗粒混合物中的分布(重力作用在岩石上)。
- 在相变点附近,流体中临界乳光的出现。
3.9.3 理论概述
1970 年代和 80 年代材料科学的重要发展之一是认识到统计场论与量子场论类似,可用于提供普适性的微观理论。核心观察是,对于所有不同的系统,相变时的行为都由连续场描述,并且相同的统计场论将描述不同的系统。所有这些系统中的标度指数(scaling exponents)都可以单独从场论中推导出来,被称为临界指数(critical exponents)。
关键的观察是,在相变或临界点附近,所有尺度都会发生扰动,因此人们应该寻找一种明确的标度不变理论来描述这种现象,这似乎首先被置于一个 Pokrovsky 和 Patashinsky 于 1965 年建立的正式理论框架中。普适性是标度不变理论相对较少这一事实的副产品。对于任何一个特定的物理系统,详细描述可能有许多与尺度相关的参数和方面。然而,随着相变的临近,与尺度相关的参数发挥的重要作用越来越小,物理描述的尺度不变部分占主导地位。因此,可以使用简化且通常可精确求解的模型来近似这些系统在临界点附近的行为。
逾渗可以通过随机电阻网络来建模,电流从网络的一侧流到另一侧。网络的总电阻被视为由网络中电阻器的平均连通性来描述。
撕裂和裂纹的形成可以通过随机的电熔丝网络来模拟。随着流经网络的电流增加,一些保险丝可能会爆裂,但总的来说,电流会在问题区域周围分流,并均匀分布。然而,在某个点(在相变时)可能会发生级联故障(cascade failure),其中一个保险丝弹出的过大电流依次使下一个保险丝过载,直到网络的两侧完全断开并且不再有电流流动。
要对此类随机网络系统进行分析,需要考虑所有可能网络的随机空间(即正则系综),并对所有可能的网络构型进行求和(积分)。与前面的讨论一样,每个给定的随机构型都被理解为是从具有某个给定概率分布的所有构型池中抽取的;温度在分布中的作用通常被网络的平均连通性所取代。
算子的期望值,如流速、热容量等,是通过对所有可能的配置进行积分得到的。这种对所有可能构型的积分行为是统计力学和量子场论系统之间的共同点。特别地,重整化群的语言可以应用于随机网络模型的讨论。在 1990 年代和 2000 年代,人们发现了统计模型与共形场论(conformal field theory)之间更紧密的联系。 普遍性研究仍然是一个重要的研究领域。
3.9.4 其他领域的应用
与统计力学中的其他概念(如熵和主方程)一样,普适性已被证明是一种有用的结构,可用于在更高级别表征分布式系统,如多主体系统(multi-agent systems)。该术语已应用于多主体模拟,其中系统表现出的系统级行为,独立于单个主体的复杂程度,几乎完全由管理它们交互的约束的性质驱动。在网络动力学中,普适性指的是尽管非线性动力学模型在许多细节上存在差异,但观察到的许多不同系统的行为都遵循一组普遍规律。这些定律独立于每个系统的具体细节。
3.10 普适类(Universality class)
在统计力学中,普适类是重整化群流(renormalization group flow)过程中,共同遵守单一标度不变限制(single scale invariant limit)的数学模型的集合。虽然同一类中的模型在有限尺度上可能存在显著差异,但随着接近限制尺度,它们的行为将变得越来越相似。特别是,临界指数等渐近现象(asymptotic phenomena)对于类中的所有模型都是相同的。
一些经过充分研究的普适性类是在其各自的相变点,包含伊辛模型或渗流理论的类;这些都是类族(families of classes),每个晶格维度一个。通常,一族普适类将具有较低和较高的临界维数(critical dimension):低于较低的临界维数,普适性类变得退化(对于 Ising 模型或定向渗流,该维数为 2 d 2d 2d,但对于无向渗流为 1 d 1d 1d),并且在上临界维度之上,临界指数稳定并且可以通过平均场理论的模拟来计算(对于 Ising 或定向渗流,该维度为 4 d 4d 4d,对于无向渗流,该维度为 6 d 6d 6d)。
3.10.1 临界指数列表
临界指数是根据系统在其相变点附近的某些物理性质的变化来定义的。这些物理特性将包括其降低的温度 τ \tau τ ,测量系统处于“有序”阶段的程度的序参量,比热等。
- 指数 α \alpha α 是比热 C C C 与降低温度之间相关的指数:我们有 C = τ − α C=\tau ^{-\alpha } C=τ−α。比热在临界点通常是奇异的,但 α \alpha α 定义中的减号允许它保持正值。
- 指数 β \beta β 与序参量 Ψ \Psi Ψ 与温度之间的关系有关。与大多数临界指数不同,它被假定为正,因为序参量在临界点通常为零。所以我们有 Ψ = ∣ τ ∣ β \Psi =|\tau |^{\beta } Ψ=∣τ∣β。
- 指数 γ \gamma γ 将温度与系统对外部驱动力或源场(source field)的响应联系起来。我们有 d Ψ / d J = τ − γ \mathrm{d}\Psi /\mathrm{d}J=\tau ^{-\gamma } dΨ/dJ=τ−γ,其中 J J J 为驱动力。
- 指数 δ \delta δ 将序参量与临界温度下的源场相关联,此时该关系变为非线性。我们有 J = Ψ δ J=\Psi ^{\delta } J=Ψδ(因此 Ψ = J 1 / δ \Psi =J^{1/\delta } Ψ=J1/δ), 含义同上。
- 指数 ν \nu ν 将相关性的大小(即有序相的斑块(patches of the ordered phase))与温度相关联;远离临界点,这些以相关长度(correlation length) ξ \xi ξ 为特征。 我们有 ξ = τ − ν \xi =\tau ^{-\nu } ξ=τ−ν。
- 指数 η \eta η 测量临界温度下相关性的大小。它被定义为相关函数(correlation function)缩放为 r − d + 2 − η r^{-d+2-\eta } r−d+2−η。
- 指数 σ \sigma σ 用于渗流理论,测量在低于临界点的“温度”(连接概率)下最大集团(粗略地说,最大有序块)的大小。 所以 s m a x ∼ ( p c − p ) − 1 / σ s_{\mathrm{max}}\sim (p_{c}-p)^{-1/\sigma } smax∼(pc−p)−1/σ。
- 指数 τ \tau τ 也来自渗流理论,测量大小为 s s s 的集团的数量,其大小远离 s m a x s_{\mathrm{max}} smax(或处于临界状态的集团数): n s ∼ s − τ f ( s / s m a x ) n_{s}\sim s^{-\tau }f(s/s_{\mathrm{max}}) ns∼s−τf(s/smax),其中 f f f 因子在临界概率下被移除。
对于对称性,列出的群给出了序参量的对称性。群 D i h n Dih_{n} Dihn 是二面体群(dihedral group), n n n 多边形的对称群, S n S_{n} Sn 为 n n n 元对称群, O c t Oct Oct 为八面体群, O ( n ) O(n) O(n) 为 n n n 维正交群。1 是平凡群。

图 临界指数列表
3.11 临界现象
3.11.1 临界点(Critical point)
wki: Critical point (thermodynamics)
wiki: Critical points of the elements (data page)
3.11.2 临界指数(Critical exponent)
wiki: Percolation critical exponents
临界指数(Critical exponents)描述了物理量在连续相变附近的行为。人们相信,虽然没有证明,但它们是普适的(universal),即它们不依赖于物理系统的细节,而只依赖于它的一些一般特征。例如,对于铁磁系统,临界指数仅取决于:
- 系统维度;
- 相互作用的范围;
- 自旋维度。
实验数据支持临界指数的这些性质。解析结果理论上可以在高维的平均场理论中获得,或者可以得出精确解,例如二维伊辛模型。一般维度的理论处理需要重整化群方法或保形自举(conformal bootstrap)技术。相变和临界指数出现在许多物理系统中,例如临界点的水、磁系统、超导性、渗流和湍流。平均场指数有效的临界尺寸因系统而异,甚至可以是无限大。
3.11.2.1 定义
驱动相变的控制参数通常是温度,但也可以是其他宏观变量,如压力或外部磁场。为简单起见,以下讨论根据温度进行,转换为另一个控制参数很简单。发生转变的温度称为临界温度 T c T_{\mathrm{c}} Tc。我们想根据临界温度附近的幂律来描述物理量 f f f 的行为;我们引入对比温度(reduced temperature):
τ : = T − T c T c {\displaystyle \tau :={\frac {T-T_{\mathrm {c} }}{T_{\mathrm {c} }}}} τ:=TcT−Tc
其在相变时为零,并定义临界指数 k k k:
k = def lim τ → 0 log ∣ f ( τ ) ∣ log ∣ τ ∣ {\displaystyle k\,{\stackrel {\text{def}}{=}}\,\lim _{\tau \to 0}{\frac {\log |f(\tau )|}{\log |\tau |}}} k=defτ→0limlog∣τ∣log∣f(τ)∣
这导致我们正在寻找的幂律:
f ( τ ) ∝ τ k , τ → 0 {\displaystyle f(\tau )\propto \tau ^{k}\,,\quad \tau \to 0} f(τ)∝τk,τ→0
重要的是要记住,这表示函数在 τ → 0 \tau\rightarrow 0 τ→0 时, f ( τ ) f(\tau) f(τ) 的渐近行为。
更一般地说,人们可能会期望
f ( τ ) = A τ k ( 1 + b τ k 1 + ⋯ ) {\displaystyle f(\tau )=A\tau ^{k}\left(1+b\tau ^{k_{1}}+\cdots \right)} f(τ)=Aτk(1+bτk1+⋯)
3.11.2.2 最重要的临界指数
让我们假设系统有两个不同的相,其特征在于序参量 Ψ \Psi Ψ,它在 T c T_{\mathrm{c}} Tc 处及以上消失。
分别考虑无序相( τ > 0 \tau>0 τ>0)、有序相( τ < 0 \tau<0 τ<0)和临界温度( τ = 0 \tau=0 τ=0)相。按照标准约定,与有序相相关的临界指数被启动。 使用上标/下标 + ( − ) + (-) +(−) 表示无序(有序)状态也是另一个标准约定。一般来说,自发对称性破缺发生在有序相中。
下方是符号的相关定义:
| Definitions | |
|---|---|
| Ψ \Psi Ψ | order parameter (e.g. ρ − ρ c ρ c \frac{\rho −\rho_{\mathrm{c}}}{\rho_{\mathrm{c}}} ρcρ−ρc for the liquid–gas critical point, magnetization for the Curie point, etc.) |
| τ \tau τ | T − T c T c \frac{T − T_{\mathrm{c}}}{T_{\mathrm{c}}} TcT−Tc |
| f f f | specific free energy |
| C C C | specific heat: − T ∂ 2 f ∂ T 2 −T\frac{\partial^{2}f}{\partial T^{2}} −T∂T2∂2f |
| J J J | source field (e.g. P − P c P c \frac{P-P_{\mathrm{c}}}{P_{\mathrm{c}}} PcP−Pc where P P P is the pressure and P c P_{\mathrm{c}} Pc the critical pressure for the liquid-gas critical point, reduced chemical potential, the magnetic field H H H for the Curie point) |
| χ \chi χ | the susceptibility, compressibility, etc.; ∂ φ ∂ J \frac{\partial \varphi}{\partial J} ∂J∂φ |
| ξ \xi ξ | correlation length |
| d d d | the number of spatial dimensions |
| < ψ ( x ) → ψ ( y ) → > \left<\psi\overrightarrow{(x)}\psi\overrightarrow{(y)}\right> ⟨ψ(x)ψ(y)⟩ | the correlation function |
| r r r | spatial distance |
以下条目在 J = 0 J = 0 J=0 处求值( δ \delta δ 条目除外)
| Critical exponents for τ > 0 \tau > 0 τ>0 (disordered phase) | |
|---|---|
| Greek letter | relation |
| α \alpha α | C ∝ τ − α C \propto \tau^{-\alpha} C∝τ−α |
| γ \gamma γ | χ ∝ τ − γ \chi\propto\tau^{-\gamma} χ∝τ−γ |
| ν \nu ν | ξ ∝ τ − ν \xi\propto\tau^{−\nu} ξ∝τ−ν |
| Critical exponents for τ < 0 \tau < 0 τ<0 (ordered phase) | |
|---|---|
| Greek letter | relation |
| α ′ \alpha' α′ | C ∝ ( − τ ) − α ′ C\propto (−\tau)^{−\alpha '} C∝(−τ)−α′ |
| β \beta β | Ψ ∝ ( − τ ) β \Psi\propto (−\tau)^{\beta} Ψ∝(−τ)β |
| γ ′ \gamma' γ′ | χ ∝ ( − τ ) − γ ′ \chi\propto (−\tau)^{-\gamma'} χ∝(−τ)−γ′ |
| ν ′ \nu' ν′ | ξ ∝ ( − τ ) − ν ′ \xi\propto (−\tau)^{−\nu'} ξ∝(−τ)−ν′ |
| Critical exponents for τ = 0 \tau=0 τ=0 | |
|---|---|
| Greek letter | relation |
| δ \delta δ | J ∝ Ψ δ J\propto\Psi^{\delta} J∝Ψδ |
| η \eta η | < ψ ( 0 ) ψ ( r ) > ∝ r − d + 2 − η \left<\psi(0)\psi(r)\right>\propto r^{−d + 2 −\eta} ⟨ψ(0)ψ(r)⟩∝r−d+2−η |
临界指数可以从比自由能(specific free energy) f ( J , T ) f(J,T) f(J,T) 导出,后者作为源和温度的函数。相关长度(correlation length)可以从泛函 F [ J ; T ] F[J;T] F[J;T] 导出。
这些关系在二维和三维系统的临界点附近是准确的。然而,在四维空间中,幂律被对数因子修正。它们不会出现在任意接近但不完全接近 4 的维度中,这可以用来解决这个问题。
3.11.2.3 类伊辛系统的平均场临界指数
标量场(伊辛模型是典型示例)的临界指数的经典朗道理论(也称为平均场理论)值由下式给出:
α = α ′ = 0 , β = 1 2 , γ = γ ′ = 1 , δ = 3 {\displaystyle \alpha =\alpha ^{\prime }=0\,,\quad \beta ={\tfrac {1}{2}}\,,\quad \gamma =\gamma ^{\prime }=1 \,,\quad \delta =3} α=α′=0,β=21,γ=γ′=1,δ=3
如果我们添加导数项将其变成平均场 Ginzburg-Landau theory,我们得到
η = 0 , ν = 1 2 {\displaystyle \eta =0\,,\quad \nu ={\tfrac {1}{2}}} η=0,ν=21
临界现象研究的重大发现之一是,临界点的平均场论只有在系统的空间维数高于某一维数时才正确,该维数称为上临界维数(upper critical dimension),其在多数情况下不包括物理维数 1、2 或 3 。平均场理论的问题在于临界指数不依赖于空间维度。这导致低于临界维度的定量差异,其中真正的临界指数与平均场值不同。它甚至会导致低空间维度上的定性差异,此时临界点实际上不再存在,尽管平均场理论仍然预测存在临界点。这是没有相变的维度 1 中的伊辛模型的情况。平均场论在定性上变得不正确的空间维度称为下临界维度(lower critical dimension)。
3.11.2.4 实验值
对于超流氦的相变(所谓的 lambda 转变),最准确的 α 测量值是 −0.0127(3)。 该值是在航天飞机上测量的,以尽量减少样品中的压力差。这个数值与通过高温膨胀技术(high temperature expansion techniques)、蒙特卡罗方法(Monte Carlo methods)和保形自举法(conformal bootstrap)得到的最精确的理论测定结果存在重大分歧
未解决的物理问题:
解释 Helium-4 中超流体转变的热容量临界指数 α \alpha α 的实验和理论确定之间的差异。
3.11.2.5 理论预测
可以通过晶格模型的蒙特卡罗模拟来评估临界指数。这种第一性原理方法的准确性取决于可用的计算资源,这决定了达到无限体积极限和减少统计误差的能力。其他技术依赖于对临界涨落(critical fluctuations)的理论理解。应用最广泛的技术是重整化群。保形自举是最近开发的一项技术,它在伊辛临界指数方面取得了无与伦比的准确性。
3.11.2.6 缩放函数(Scaling functions)
鉴于临界尺度,我们可以用无量纲量重新表达所有热力学量。足够接近临界点,一切都可以根据减少量的幂的特定比率重新表达。这就是缩放函数。
缩放函数的起源可以从重整化群中看出。临界点是红外固定点(infrared fixed point)。在临界点足够小的邻域内,我们可以线性化重整化群的作用。这基本上意味着将系统重新缩放因子 a a a,将等同于将运算符(operators)和源场(source fields)重新缩放为某个 Δ \Delta Δ 的一个 a Δ a^{\Delta} aΔ 因子。因此,我们可以根据重新缩放的比例无关量重新参数化所有量。
3.11.2.7 比例关系
长期以来,人们认为临界指数在临界温度之上和之下是相同的,例如 α ≡ α ′ \alpha\equiv \alpha' α≡α′ 或 γ ≡ γ ′ \gamma\equiv\gamma' γ≡γ′。现在已经表明,这不一定是正确的:当连续对称性(continuous symmetry)被不相关的(在重整化群意义上)各向异性明确分解为离散对称性(discrete symmetry)时,指数 γ \gamma γ 和 γ ′ \gamma' γ′ 不相同。
临界指数用希腊字母表示。它们属于普适类,并服从缩放(scaling)和超缩放关系(hyperscaling relations)
ν d = 2 − α = 2 β + γ = β ( δ + 1 ) = γ δ + 1 δ − 1 2 − η = γ ν = d δ − 1 δ + 1 \begin{aligned} \nu d&=2-\alpha =2\beta +\gamma =\beta (\delta +1)=\gamma {\frac {\delta +1}{\delta -1 }}\\ 2-\eta &={\frac {\gamma }{\nu }}=d{\frac {\delta -1}{\delta +1}} \end{aligned} νd2−η=2−α=2β+γ=β(δ+1)=γδ−1δ+1=νγ=dδ+1δ−1
这些方程意味着只有两个独立的指数,例如 ν ν ν 和 η \eta η。所有这些都来自重整化群的理论。
3.11.2.8 渗流理论(Percolation theory)
相变和临界指数也出现在渗流过程中,其中晶格中“被占据”的位置(site)或链接(link)的浓度是相变的控制参数(与物理学中经典相变中的温度类比)。
最简单的例子之一是二维方晶格中的伯努利渗流(Bernoulli percolation)。位点被随机占用的概率为 p p p。集团(cluster)被定义为最近相邻的已占用位点的集合。对于较小的 p p p 值,被占用的位点只形成小的局部集团。在渗流阈值(percolation threshold)处 p c ≈ 0.5927 p_{c}\approx 0.5927 pc≈0.5927(也称为临界概率(critical probability),形成了横跨系统相反位置的跨越集团(spanning cluster),并且我们得到了以普适临界指数为特征的二阶相变。对于渗流,普适类与 Ising 普适类不同。例如,对于 2D 伯努利渗流,相关长度临界指数为 ν = 4 / 3 \nu =4/3 ν=4/3,相比而言,二维 Ising 模型的临界指数为 ν = 1 \nu = 1 ν=1。
3.11.2.9 各向异性
有一些各向异性系统,其中相关长度与方向有关。
定向渗流也可以看作是各向异性渗流。在这种情况下,临界指数不同,上限临界维数为 5。
3.11.2.10 多临界点(Multicritical points)
更复杂的行为可能发生在多临界点(Multicritical points)、临界流形(critical manifolds)的边界或交叉点。它们可以通过调整两个或多个参数的值来达到,例如温度和压力。
3.11.2.11 静态与动态属性
上述示例专门针对关键系统的静态属性。然而,系统的动态特性也可能变得至关重要。特别是,系统的特征时间 τ c h a r \tau_{\mathrm{char}} τchar 发散为 τ c h a r ∝ ξ z \tau_{\mathrm{char}}\propto\xi^{z} τchar∝ξz,具有动态指数 z z z。此外,如果要求动态指数也相同,则具有相同静态临界指数的等效模型的大静态普适类会分解为较小的动态普适类。
临界指数可以从共形场论(conformal field theory)中计算出来。
另见异常缩放维度(anomalous scaling dimension)。
3.11.2.12 自组织临界
耗散系统的自组织临界性也存在临界指数。
3.11.3 临界乳光(Critical opalescence)
3.11.4 临界维度(Critical dimension)
3.11.5 Widom scaling
3.11.6 Conformal bootstrap
3.11.7 Conformal field theory
4. 无标度网络(Scale-free network)
标度不变(scale invariance)则从函数构造的角度,当因变量 x x x 比例缩放时,函数本身会比例的标度缩放,即 f ( a x ) = a n f ( x ) f(ax)=a^{n}f(x) f(ax)=anf(x), 因此,每个幂指数对应的幂律函数都只是其他情况的缩放而已。
无标度(scale-free)主要侧重在幂指数 β \beta β 不同条件下,其均值、方差和不同的矩的 infinty 情况。
国内复杂网络教材有时候基本一个意思,没有太多的区分,都说是无标度。在国外专门的数学统计书或者期刊上有这层意思。
简单来说:scale-free 和 scale invariant 表达的是同一定义。即一个:
‘property invariant under scale transformations’ or ‘property free from scale transformations’。
实际上在早于复杂网络的研究之前统计物理学界里 scale-free 和 scale invariant 就常常混着用了。
在复杂网络的研究当中,scale-free 就比较特指幂率分布的 scale-free network。个人认为是因为最早 Barabasi & Albert 的文章中使用了 scale-free network 的命名。而 scale invariant 就泛指 scale invariance 这一个更加大的概念了。
- 参考文献
百度百科: 标度
wiki: Universality (dynamical systems)
赵凯华. 力学. 2004.
























 1942
1942

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








