记一下机器学习笔记 核方法与径向基函数网络

这里算是《神经网络与机器学习》第5章的笔记。
其实本章主打的是还是径向基函数，关于核方法的内容不多。

核方法的想法就是，把原来线性不可分的样本通过某种非线性变换映射到合适的高维特征空间，使之方便用线性学习器来处理。
径向基函数网络是一种实现方式，其结构类似于单一隐藏层的神经网络，原理是在隐藏层用径向基函数将数据映射到高维特征空间，然后再在输出层对其输出进行线性分类。
这招最经典的应用便是支持向量机。

Cover定理

Cover定理说白了就是：把一堆线性不可分的数据非线性地映射到一个维度更高的空间，没准就变得线性可分了。

首先，输入的数据样本集为一组N个$m_0$维的向量$\textbf x_1,\textbf x_1,...,\textbf x_N$，每个样本都被归类到两个类$C_1$和$C_2$之一。
定义一组实值函数（也就是输入一个向量输出一个实数的函数）$\varphi_1(\textbf x),\varphi_2(\textbf x), ... ,\varphi_{m_1}(\textbf x)$，用来将输入数据映射到一个$m_1$维的空间，将它们组成一个向量：

$$\phi = \left[ \varphi_1(\textbf x),\varphi_2(\textbf x), \cdots ,\varphi_{m_1}(\textbf x)\right]^T$$

这个函数向量$\phi$的输出可被认为是被映射到高维空间之后的输入数据$\textbf x$。$\varphi_i(\textbf x)$称为隐藏函数，其组成的向量$\phi$所在的空间称为隐藏空间或特征空间。

如果有那么个$m_1$维的向量$\textbf w$，使得这个成立：

$$\textbf w^T \phi(\textbf x)>0, \textbf x \in C_1;$$ $$\textbf w^T \phi(\textbf x)<0, \textbf x \in C_2;$$
也就是说被 $\phi$映射到另一个高维空间的数据样本们成了线性可分的，就说这个把 $\textbf x$分类到 $C_1$和 $C_2$的分法是 $\phi$可分的。
对于 $\textbf x$来说， $\textbf w ^T \phi (\textbf x)=0$就是一个分类曲面。

于是模式可分性的Cover定理在这就包含这两部分：

• 隐藏函数的非线性转换。
• 高维的特征空间（这个高维是相对原始数据的维度来说的，由隐藏函数的个数决定）。

异或问题

拿异或问题举个栗子。因为是个典型的线性不可分问题。
其点(0,0)和(1,1)归于类0，点(0,1)和点(1,0)归于类1。

然后我们要拿一组隐藏函数将这些点映射到零一空间里。
在这里使用高斯隐藏函数。因为问题简单，所以只用了两个隐藏函数，维度没有增加，不过够用了：

$$\varphi_1(\textbf x) = exp(-\lVert \textbf x - \textbf t_1 \rVert^2)$$ $$\varphi_2(\textbf x) = exp(-\lVert \textbf x - \textbf t_2 \rVert^2)$$
其中 $\textbf t_1 = (1,1)$， $\textbf t_2 = (0,0)$。也就是拿样本点跟这俩点的几何距离作为高斯函数的自变量。
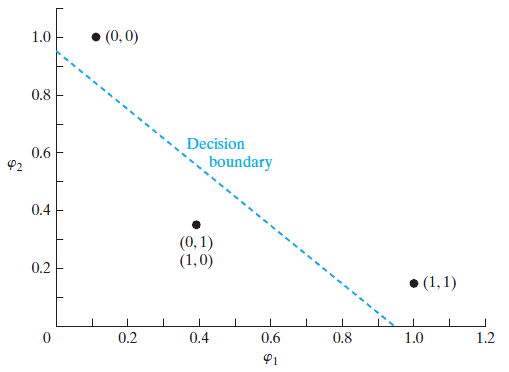
转换出来这个样子。

转换前	转换后
(1,1)	(1.0000, 0.1353)
(0,1)	(0.3678, 0.3678)
(0,0)	(0.1353, 1.0000)
(1,0)	(0.3678, 0.3678)

图画出来一看，线性可分了。

这就是传说中的核技巧。

径向基函数网络

插值问题

其实单一输出变量的机器学习问题可以理解成这么一个插值问题（可以拿地统计里的空间插值理解）：

• 训练阶段就是找出这么个曲面： $$F(\textbf x_i) = d_i, \qquad i = 1,2,\cdots,N$$
• 泛化阶段就是在这曲面上插值。

这里用的解决方案就是径向基函数（Radial-Based Function，RBF）技术。
其给出的$F(\textbf x)$的形式为：

F