点云轮廓点排序——旋转角法（python pycharm）

一、背景介绍

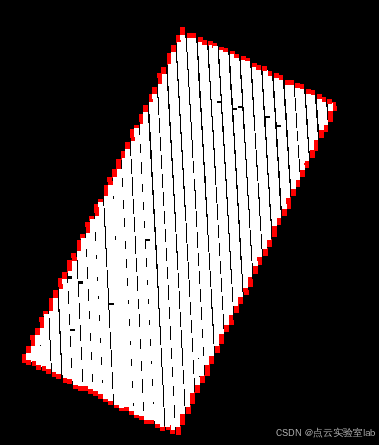
      很多边缘提取算法提取的边缘点为无序点云，如下图所示，无序点云不利于后续各种应用，比如根据边缘计算点云面积、点云轮廓线规则化等。若对点云进行排序，则可以进行上述应用。但实际上，点云形状错综复杂，对点云进行排序难度会比较大。此次博客介绍一种针对简单形状点云的边缘点排序原理，对于复杂形状点云，仅供参考。

二、旋转角大小排序

       对于形状简单的点云，可以使用与某一方向的夹角，按照夹角大小进行排序，实现点的排序，如下图所示。如图所示，以y轴为起始旋转角开始的地方，每个轮廓点与以轴构成的旋转角不一致，按照旋转角从小到大进行排序，可以实现轮廓点的排序。

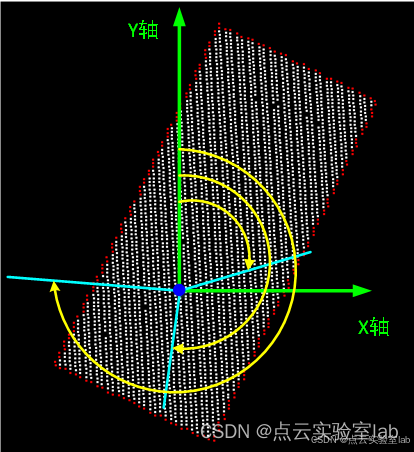
   基于这一原理，具体步骤如下：

（1）中心计算：统计所有点的平均坐标作为中心

（2）计算旋转角：以y轴为起始方向，计算每个轮廓点与y轴的夹角，得到夹角集合

（3）角度排序：对角度从小到大进行排序，按照排序后的角度对轮廓点进行排序，即实现角度排序

三、测试

3.1 测试数据说明

     数据格式如图，x  y  z  r  g  b，其中边缘点用红色表示，其r g b值为255  0 0。非边缘点用白色表示，其r g b值为255 255 255。

3.2 原始轮廓点直接连线

      直接将文件中边缘轮廓点直接相连，结果如下。表明点之间是无序结构，直接连轮廓点，无法反应点云真实形状。

3.3 轮廓点排序后结果

      可以发现，对轮廓点进行排序后，构成的多边形能够较准确反应点云形状，局部放大图中，也可以看到轮廓点为有序结构。

排序后直接相连	局部放大	局部放大

四、源代码下载

根据上述介绍的原理，基于python、pycharm进行实现，包括测试数据与代码，下载链接地址：https://download.csdn.net/download/qq_32867925/90245007?spm=1001.2014.3001.5503

其中包含2个测试，一个为未排序时的结果，轮廓点无序；后一个为排序后结果。