Ornstein-Uhlenbeck过程

在强化学习中（如DDPG算法），可能会用到Ornstein-Uhlenbeck（奥恩斯坦-乌伦贝克）过程，即OU过程。

这篇博客将从三个角度解释一下OU过程：

1. 什么是OU过程？
2. OU过程适用于哪些场景？
3. OU过程的验证实验

前言： DDPG论文中使用Ornstein-Uhlenbeck噪声用于探索，为什么不用高斯噪声呢？

1. OU过程定义

OU过程有下面的随机微分方程：$$d{x}_t=\theta (\mu -x_t)dt+\sigma d{W}_t$$ 其中，其中$\theta >0$，$\mu$（均值），$\sigma >0$（方差）均为参数，$W_t$ 为维纳过程（布朗运动）。

---

可以将OU过程表达为离散形式研究一下，暂且不考虑第二项（扰动项）：
$$d{x}_t=x(t+\Delta t)-x(t)=-\theta (x_t-\mu )\Delta t$$ 可以发现，OU过程是均值回归过程，当 $x_t$ 比均值 $\mu$ 大的时候，下一步状态值$x_{t+\Delta t}$就会变小；反之，下一步状态值会变大。简单地说就是状态值偏离均值的时候会被拉回。

---

那么$\theta >0$，$\mu$，$\sigma >0$ 各个参数有什么作用呢？先看结论：

现在对OU过程有下面的随机微分方程 $d{x}_t=\theta (\mu -x_t)dt+\sigma d{W}_t$
进行分析，这显然是一个一阶线性微分方程，求解过程如下：

注：求解过程中用 $\alpha$ 表示 $\mu$，用 $\beta$ 表示 $\theta$。

不考虑维纳过程，可以得到：$$x_t=\mu +(x_0-\mu )e^{-\theta t}$$ 所以 $\theta$ 表示系统对干扰的反映程度，即 $\theta$ 越大，干扰变得越小，保持状态值在均值附近。

再考虑扰动项（维纳过程），每一段时间间隔内的增量是服从高斯分布的：
$$W(t)-W(s)\sim N(0,{\sigma }^2(t-s))$$ 所以 方差$\sigma$ 表示噪音的大小或变化，即决定扰动的变化尺度。

2. OU过程适适用场景

OU过程是时序相关的，所以在强化学习的前一步和后一步的动作选取过程中可以利用OU过程产生时序相关的探索，以提高在惯性系统（即环境）中的控制任务的探索效率。（注：高斯噪声是时序上不相关的，前一步和后一步选取动作的时候噪声都是独立的。前后两动作之间也只是通过状态使其独立。）
所以OU过程的适用场景有：

1. 相比于独立噪声，OU噪声适合于惯性系统，尤其是时间离散化粒度较小的情况。
2. 可以保护实际系统，如机械臂。

本部分参考知乎专栏强化学习中Ornstein-Uhlenbeck噪声是鸡肋吗？

3. OU过程实验

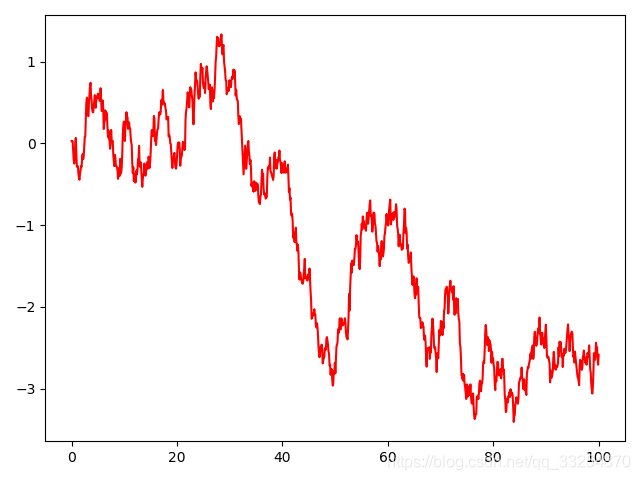
import numpy as np
import matplotlib.pyplot as plt


class OrnsteinUhlenbeckActionNoise:
    def __init__(self, mu, sigma=1.0, theta=0.15, dt=1e-2, x0=None):
        self.theta = theta
        self.mu = mu
        self.sigma = sigma
        self.dt = dt
        self.x0 = x0
        self.reset()

    def __call__(self):
        x = self.x_prev + self.theta * (self.mu - self.x_prev) * self.dt + \
            self.sigma * np.sqrt(self.dt) * np.random.normal(size=self.mu.shape)
        self.x_prev = x
        return x

    def reset(self):
        self.x_prev = self.x0 if self.x0 is not None else np.zeros_like(self.mu)

    def __repr__(self):
        return 'OrnsteinUhlenbeckActionNoise(mu={}, sigma={})'.format(self.mu, self.sigma)


if __name__ == "__main__":
    ou_noise = OrnsteinUhlenbeckActionNoise(mu=np.zeros(1))
    plt.figure()
    y1 = []
    y2 = np.random.normal(0, 1, 1000)
    t = np.linspace(0, 100, 1000)
    for _ in t:
        y1.append(ou_noise())

    # plt.plot(t, y1, c='r')
    plt.plot(t, y2, c='b')
    plt.show()

从上面结果可以很清楚地区分了OU过程的时序相关性与高斯随机过程的前后无关性。OU noise往往不会高斯噪声一样相邻的两步的值差别那么大，而是会绕着均值附近正向或负向探索一段距离，就像物价和利率的波动一样，这有利于在一个方向上探索。