【线性代数复习笔记】同济大学版第三章和第四章 矩阵的初等变换与线性方程组与向量组的线性相关性

1.矩阵的初等变换

矩阵的三种初等变换及性质

行阶梯形矩阵

对行最简形矩阵再施以初等列变换，可变为形状更简单的矩阵，称为标准型：

矩阵的初等变换的性质

---

性质二的推论：

2.矩阵的秩

矩阵子式定义：

---

矩阵的初等变换并不改变矩阵的秩：

矩阵的秩的定义：

可逆矩阵的秩等于矩阵的阶数，故可逆矩阵又叫做满秩矩阵，不可逆矩阵（奇异矩阵）又称降秩矩阵。

---

定理2的推论：

---

矩阵的秩的性质

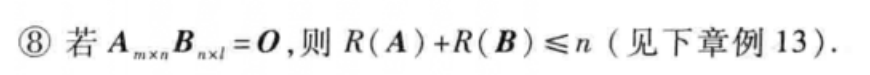
3.线性方程的解

由定理3得到的推论：

---

第四章分界线

1.向量组及其线性组合

补充：单位坐标向量：

2.向量组的线性相关性

推论：

补充：n维单位坐标向量组是线性无关的。

线性相关性的一些重要结论

看着真懵啊。。。。

3.向量组的秩

最大无关组有很多个。

---

根据向量组的秩的定义和定理6可以得到：


以上为定理2和定理3的重述

4.线性方程组的解的结构

线性齐次方程

---

线性非齐次方程

---

5.向量空间

下面这两个例题可以很好的帮助理解定义6

---