1.3 傅里叶变换介绍4-离散傅里叶变换

一、定义离散序列x[n]的傅里叶变换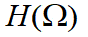

       对于线性非时变系统，把x(t)分解成一些列子信号（子信号要简单)，然后得到各子信号的响应(子信号的响应要容易求出），然后综合出来就是输出y(t).

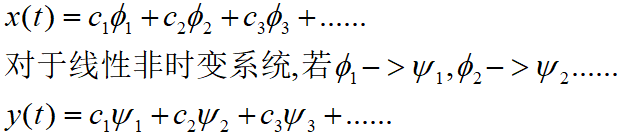
        对于连续系数系统，选择指数函数作为子系统，

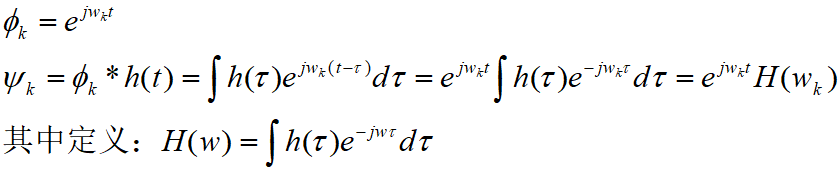
     对于离散系统，同样选择指数函数作为子系统

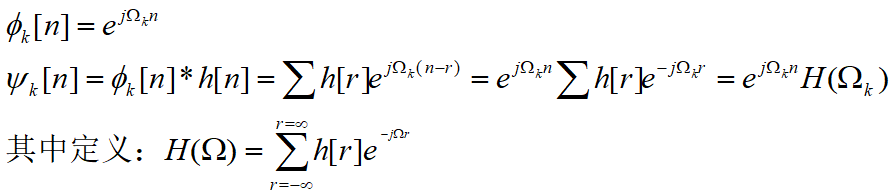
二、周期离散序列的离散傅里叶级数分解：

        周期离散函数离散傅里叶级数以及逆变换公式如下：

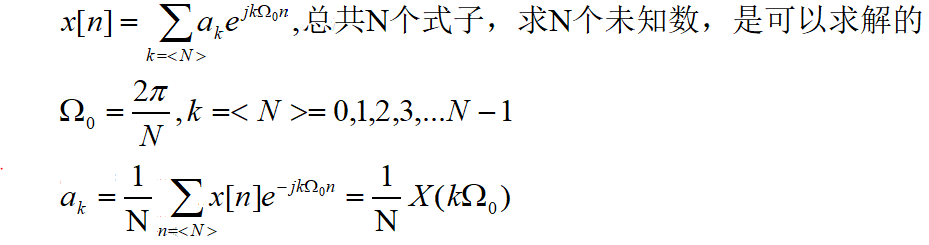
【例1】举例说明上述子信号是在k=N/2时角频率最大，

【例2】见附录1，进行高频滤波的一种做法。

三、非周期离散函数的离散傅里叶变换公式：

        同样先把非周期离散函数x(n)周期化为，然后把周期增大到正无穷，推如下：

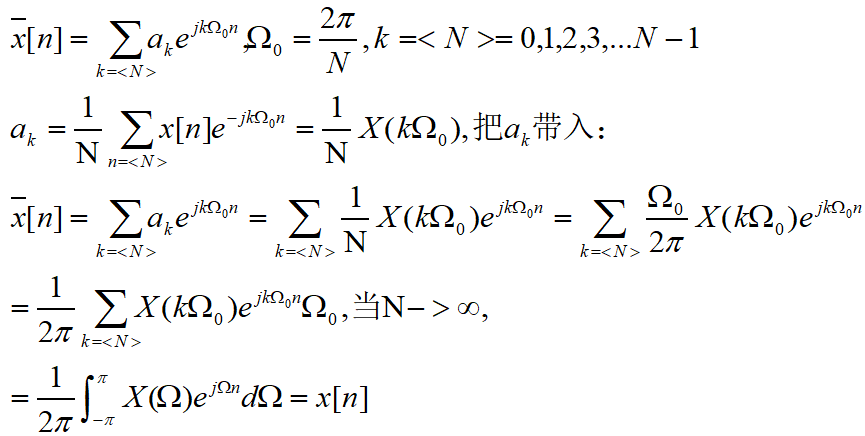
总结如下，非周期离散序列的傅里叶变换如下：

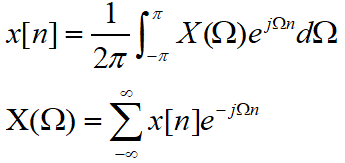
四、一个例子

[例]求的傅里叶变换：a>0.

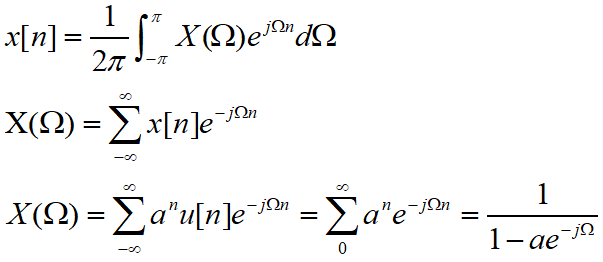
当a=0.6时，其图像如下，可以见X是周期性的，周期为2Pi.

import cmath
import numpy as np
import matplotlib.pyplot as plt

a=0.6
w=[]
F = []
pi=3.141592
for theta in np.arange(-10,10,0.1):
    w.append(theta)
    res = 1/(1-a*cmath.exp(complex(0,-theta)))
    F.append(abs(res))
plt.plot(w,F, color='blue')
plt.show()

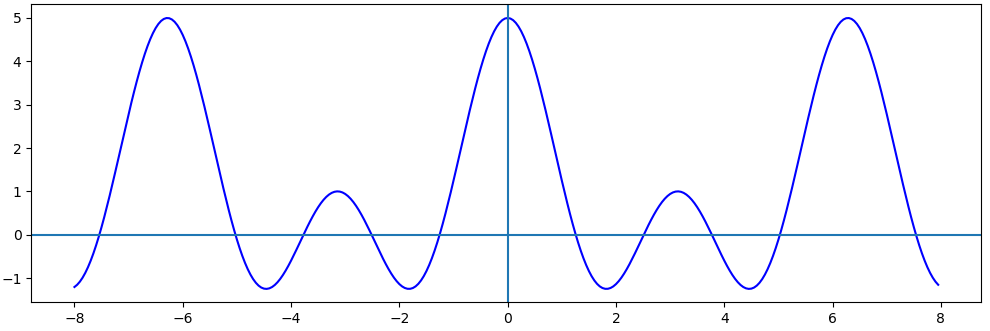
【例2】方波的一个信号。x[n]=1,  n>=-2且n<=2时，其离散傅里叶变换的幅值曲线如下图：

起始

import cmath
import numpy as np
import matplotlib.pyplot as plt

N=2
w=[]
F = []
pi=3.141592
for theta in np.arange(-8,8,0.05):
    w.append(theta)
    sum=0
    for n in [-2,-1,0,1,2]:
        sum=sum+cmath.exp(complex(0,-n*theta))
    F.append(sum.real)
plt.plot(w,F, color='blue')
plt.axvline()
plt.axhline()
plt.show()

五、周期序列的x[n]的傅里叶变换

定义如下：

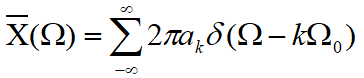
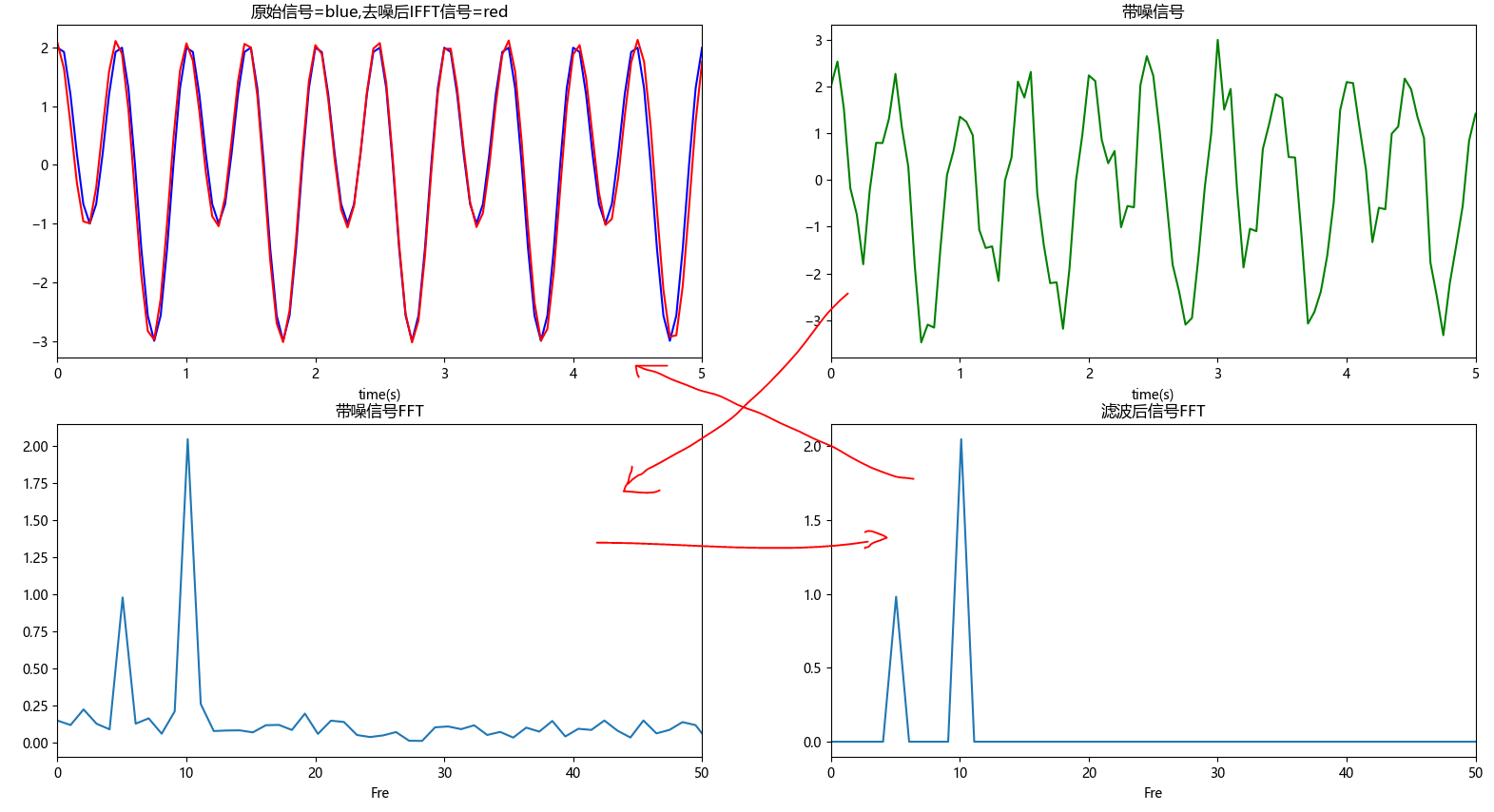
【附录1】数字序列的滤波

        通过把数字序列（原始序列+噪声）分解得到子信号以及其系数,把其中高频的子信号系数设置为0（去除噪声），重新逆变换得到新的数字序列，和原始序列非常一致。

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
sample_rate = 101
t = np.linspace(0, 5, sample_rate)
print(t)
fre1 = 1
fre2 = 2
sig = np.sin(2 * np.pi * fre1 * t) + 2 * np.cos(2 * np.pi * fre2 * t)  # 原始信号
noise = np.random.normal(0, 0.5, len(sig))
sig_noise = sig + noise  # 带噪信号
#   绘制原始信号
plt.figure(figsize=(20, 10))
plt.subplot(2, 2, 1)
plt.plot(t, sig, color='blue')
plt.xlim(0, 5)
plt.xlabel("time(s)")
plt.title("原始信号=blue,去噪后IFFT信号=red")
#   绘制带噪信号

plt.subplot(2, 2, 2)
plt.plot(t, sig_noise, color='green')
plt.xlim(0, 5)
plt.xlabel("time(s)")
plt.title("带噪信号")
#   计算并绘制带噪信号的FFT频域图

n_fft = 101
fre = np.linspace(0, sample_rate / 2, int(n_fft / 2) + 1)
sig_noise_fft = np.fft.rfft(sig_noise, n_fft)
sig_noise_fft_abs = np.abs(sig_noise_fft) * 2 / n_fft
plt.subplot(2, 2, 3)
plt.plot(fre, sig_noise_fft_abs)
plt.xlim(0, 50)
plt.xlabel("Fre")
plt.title("带噪信号FFT")

#   对带噪信号滤波并绘制FFT频域图

found_fre = np.where(sig_noise_fft_abs < 0.5)  # 滤波：判定数组内abs<0.3的值为噪声，并抽取其数组索引
filter_sig_noise_fft = sig_noise_fft.copy()
filter_sig_noise_fft[found_fre] = 0  # 滤波：将抽取的数组索引对应的FFT值赋0，去噪
filter_sig_noise_fft_abs = sig_noise_fft_abs.copy()
filter_sig_noise_fft_abs[found_fre] = 0
plt.subplot(2, 2, 4)
plt.plot(fre, filter_sig_noise_fft_abs)
plt.xlim(0, 50)
plt.xlabel("Fre")
plt.title("滤波后信号FFT")
#   对滤波后的带噪信号进行IFFT并绘制时域图与原信号对比

filter_sig_noise_ifft = np.fft.irfft(filter_sig_noise_fft, 101)
plt.subplot(2, 2, 1)
plt.plot(t, filter_sig_noise_ifft, color='red')
plt.xlim(0, 5)
plt.show()