Large Scale Spectral Clustering with Landmark-Based Representation

论文：AAAI 2011

代码：Julia

基于锚点的谱聚类
核心： 选取一个较小的anchor集【通常为原始数据点的子集】，计算所有数据点和anchor集之间的相似度，减少相似度矩阵维度 or 使得相似度矩阵稀疏化【导致拉普拉斯矩阵也是稀疏的，从而更高效地计算出谱】。

摘要

由于谱聚类的时间复杂度过高导致其无法在大数据集上应用，因此出现了很多改进的方法：比如使用采样策略减少数据的尺寸，或者是减少特征分解步骤的时间复杂度。对于采样的方法，虽然它们很有效，但代价是在采样过程损失了数据的结构信息。

本文提出了一个名为LSC(Landmark-based Spectral Clustering)的可扩展的谱聚类算法，其核心思想是选取p(p<<n)个代表性数据点作为landmark，将剩余数据点表示为这些landmark的线性组合，然后使用基于landmark的表示有效地计算数据的谱嵌入(spectral embedding)。并且整体的算法时间复杂度与输入呈线性关系，构图需要$O(pnm)$，计算特征值需要$O(p^3+p^{2}n)$。

算法流程： 首先在数据集X中随机选取或者利用K-Means选取p个landmark；计算landmark与剩余数据之间相似度矩阵$Z$；计算得到$Z{Z}^T$的前k个特征向量A，并根据公式【详见原文】得到最终的特征向量$B$；将$B$中每一行视为一个数据点，执行k-means聚类得到最终的结果。

Landmark-based Spectral Clustering

我们尝试设计具有如下性质的亲和矩阵：
$$W={\hat{Z}}^T\hat{Z}\hat{Z}\in R^{p\times n},p<<n\text{\hspace{1em}(1)}$$

Landmark-based Sparse Coding

数据矩阵 $X=[x_1,\cdot \cdot \cdot ,x_n]\in R^{m\times n}$，矩阵分解可以将X近似分解为 $U\in R^{m\times p}$、$Z\in R^{p\times n}$
$X\approx UZ$
U的每一列都可以被视为一个基向量，它捕捉数据中更高层次的特征，Z的每一列都是原始输入相对于新基的p维表示。测量近似值的常用方法是通过矩阵Frobenius范数||·||。因此，矩阵分解可以定义为如下优化问题：
$$\underset{U,Z}{\min }||X-UZ|{|}^2\text{\hspace{1em}(2)}$$

由于每个基向量(U的列向量)都可以看作是一个概念，稠密矩阵Z表示每个数据点都是所有概念的组合。这与我们的常识相反，因为大多数数据点只包括几个语义概念。稀疏编码(SC)是最近流行的一种矩阵分解方法，试图解决这个问题。稀疏编码在优化问题(2)中增加了Z的稀疏约束，具体来说就是A的每一列。这样SC就可以学习到一个稀疏表示。SC在数据表示方面有几个优势。首先，它产生稀疏表示，这样每个数据点被表示为少量基向量的线性组合。因此，数据点可以以一种更优雅的方式解释。其次，稀疏表示自然是一种允许快速检索的索引方案。第三，稀疏表示可以过完备，提供了广泛的生成元素。广泛的范围可能会使信号表示更加灵活，在信号提取和数据压缩等任务中更有效。

然而，求解具有稀疏约束的优化问题(2)非常耗时。现有的大多数方法都是迭代计算U和Z。显然，这些方法不能用于光谱聚类。

基向量(U的列向量)与原始数据点具有相同的维数。我们可以将基向量作为数据集的地标点。从数据集中选择地标点最有效的方法是随机抽样。除了随机选择外，还提出了几种路标点的选择方法。例如，我们可以使用k-means算法先对所有的数据点进行聚类，然后以聚类中心作为里land-mark点。但是，这些方法中的许多都是计算昂贵的，并且不能扩展到大型数据集。因此，我们将重点放在随机选择方法上，尽管在我们的实证研究中提出了随机选择和基于k-means的地标选择之间的比较。

假设我们已经有了地标矩阵U，我们可以通过求解优化问题(2)来计算表示矩阵z。通过固定U，优化问题成为一个约束(稀疏约束)线性回归问题。有很多算法可以解决这个问题。然而，这些优化方法仍然很耗时。在我们的方法中，我们简单地使用Nadaraya-Watson核回归来计算表示矩阵Z。

对于任何数据点$x_i$，我们通过下式得到近似的 ${\hat{x}}_i$,
$${\hat{x}}_i=\sum _{j=1}^p{z}_{ji}{u}_j\text{\hspace{1em}(3)}$$
$u_j$是$U$的第$j$列。这里假设，当$x_i$更接近$u_j$，$z_{ji}$应该更大；$u_j$不是$x_i$的$r(\le p)$近邻，$z_{ji}=0$这种限制自然会导致稀疏表示矩阵Z。$U_{<i>}\in R^{m\times r}$是由$x_i$的$r$个最近 landmarks 组成的$U$的子矩阵。$z_{ji}$的计算公式：

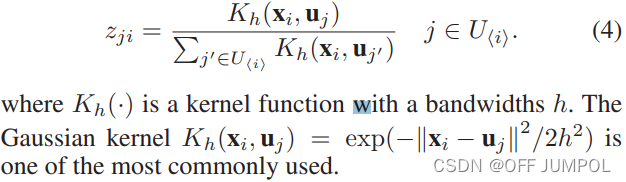
Spectral Analysis on Landmark-based Graph

我们有基于landmark的稀疏表示$Z\in R^{p\times n}$ 现在，我们简单地计算图矩阵：

$$W={\hat{Z}}^T\hat{Z}\text{\hspace{1em}(5)}$$
可以进行非常有效的特征分解。在算法中，我们选择 $\hat{Z}=D^{-1/2}Z$，其中$D$是Z的行的和。注意在上一节中，$Z$的每一列和为1，因此$W$的度矩阵为$I$，即图被自动归一化。
对$\hat{Z}$进行SVD（奇异值分解）分解：

参考链接：
初探“谱聚类”算法（无公式）