Abstract
本文主要研究谱聚类中亲和矩阵的归一化问题。我们表明,N-cuts和Ratio-cuts之间的区别在于在寻找与输入亲和矩阵最接近的双随机矩阵时所使用的误差度量(相对熵与L1范数)。然后,我们开发了一种利用冯-诺伊曼连续投影引理在Frobenius范数下寻找最优双随机逼近的方案。新的归一化方案简单有效,提供了优于许多标准化测试的聚类性能。
1 Introduction
将数据点划分为许多不同的集合的问题,称为聚类问题,是数据分析和机器学习的核心问题。通常,聚类的图论方法从测量成对亲和度Kij开始,测量点xi, xj之间的相似度,然后是标准化步骤,然后是提取主要特征向量,这些特征向量形成一个嵌入式坐标系,从中可以很容易地获得分区。在这个领域中,成功聚类有三个主要维度:(i)亲和度量,(ii)亲和矩阵的归一化,以及(iii)特定的聚类算法。通常的实践表明,前两者对性能的影响很大,而聚类过程本身的细节对性能的影响相对较小。
在本文中,我们主要研究了关联矩阵的归一化。我们首先表明,现有的流行方法Ratio-cut(参见[1])和normalization -cut[7]采用了一种隐式归一化,该归一化对应于亲和矩阵K对双重随机矩阵的L1和基于相对熵的近似。然后,我们引入了一种基于简单连续投影格式的Frobenius范数(L2)归一化算法(基于Von-Neumann的[5]连续投影引理,用于寻找子空间的最近交集),该算法在最小二乘误差范数下找到最近的双随机矩阵。我们展示了各种归一化方案对大量数据集的影响,并表明新的归一化算法通常会在标准化测试中引起显着的性能提升。综上所述,我们为聚类算法引入了一个新的调优维度,从而可以更好地控制聚类性能。
2.双随机标准化的作用
过去已经表明[11,4]K-means和谱聚类密切相关,特别是[11]表明,常用的亲和矩阵归一化(如normalize -cuts所采用的)与K-means引起的双随机约束有关。由于这一背景是我们工作的关键,我们将简要介绍相关的论点和推导。
x i ∈ R N x_i \in R^N xi∈RN 是数据点,划分为 k k k 个簇 ψ \psi ψ,每个簇 ψ j \psi_j ψj内有 n j n_j nj个点, K i j = κ ( x i , x j ) K_{ij} = \kappa (x_i,x_j) Kij=κ(xi,xj) 是对称半正定的亲和函数,如 K i j = e x p ( − ∥ x i − x j ∥ 2 / σ 2 ) K_{ij} = exp(-\begin{Vmatrix} x_i-x_j \end{Vmatrix}^2/\sigma^2 ) Kij=exp(− xi−xj 2/σ2)
然后,通过最大化找到集群分配的问题,即让簇内的点相似度更高,
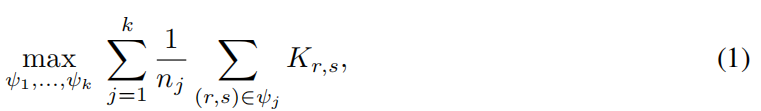
相当于最小化“kernel K-means”问题,即最小化每个簇内的点与簇的中心点的距离,
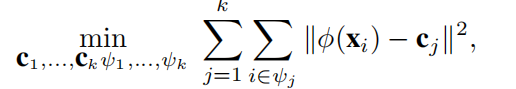
其中,
ϕ
(
x
i
)
\phi(x_i)
ϕ(xi) 是一个与核相关联的映射
κ
(
x
i
,
x
j
)
=
ϕ
(
x
i
)
T
ϕ
(
x
j
)
\kappa (x_i,x_j) = \phi(x_i)^T \phi(x_j)
κ(xi,xj)=ϕ(xi)Tϕ(xj),
c
j
=
∑
i
∈
ψ
j
ϕ
(
x
i
)
/
n
j
c_j = \sum_{i∈ψ_j} \phi(x_i) / n_j
cj=∑i∈ψjϕ(xi)/nj 是簇的中心。
经过一些代数操作,可以证明公式1 的优化设置,相当于矩阵形式: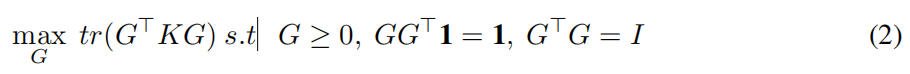
G
i
j
=
{
0
o
t
h
e
r
w
i
s
e
1
n
j
i
∈
ψ
j
G_{ij}= \begin{cases} 0& {otherwise}\\ \frac{1}{\sqrt{n_j}}& { i \in ψ_j} \end{cases}
Gij={0nj1otherwisei∈ψj
注意,矩阵 F = G G T F = GG^T F=GGT必须是双随机的(F是非负、对称的,F1 = 1,1是一个全为1的列向量)。
双随机矩阵是非负实数方阵,每个行和列求和均为1。
G 的形式和 RatioCut 的指示向量H表达式一样,但是约束条件不一样, s . t . H T H = I s.t. H^TH = I s.t.HTH=I
RatioCut
h i j = { 0 v i ∉ A j 1 ∣ A j ∣ v i ∈ A j h_{ij}= \begin{cases} 0& { v_i \notin A_j}\\ \frac{1}{\sqrt{|A_j|}}& { v_i \in A_j} \end{cases} hij={0∣Aj∣1vi∈/Ajvi∈Aj
综上所述,我们希望找到一个尽可能接近输入矩阵 K K K 的双随机矩阵 F F F(也就是说,尽可能的让 ∑ i j F i j K i j \sum_{ij} F_{ij}K_{ij} ∑ijFijKij 最大),使得对称分解 F = G G T F = GG^T F=GGT满足非负性(G≥0)和正交性约束( G T G = I G^TG = I GTG=I)。
t r ( G T K G ) = t r ( G G T K ) = t r ( F K ) = ∑ F i i K i i tr(G^TKG)=tr(GG^TK)=tr(FK)=\sum F_{ii}K_{ii} tr(GTKG)=tr(GGTK)=tr(FK)=∑FiiKii ,不知道是不是文章写错了
t r ( A B C ) = t r ( B C A ) = t r ( C A B ) tr(ABC) = tr(BCA) = tr(CAB) tr(ABC)=tr(BCA)=tr(CAB) 迹的循环性
为了看到与谱聚类的联系,特别是与N-cuts的联系,放宽公式2的非负性条件。定义一个两阶段的方法:找到最接近
K
K
K 的双随机矩阵
K
′
K'
K′ ,我们剩下一个谱分解问题:
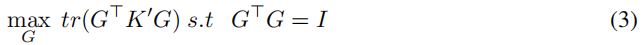
其中
G
G
G 包含
K
′
K'
K′ 的前k个特征向量。我们将把
K
K
K 变换成
K
′
K'
K′ 的过程称为一个归一化步骤。在N-cuts中,归一化的形式为
K
′
=
D
−
1
/
2
K
D
−
1
/
2
K'= D^{−1/2}KD^{−1/2}
K′=D−1/2KD−1/2 ,其中
D
=
d
i
a
g
(
K
D = diag(K
D=diag(K1
)
)
) (包含K的行和的对角矩阵)[9]。在[11]中表明,重复N-cuts归一化,即设置迭代步骤
K
(
t
+
1
)
=
D
−
1
/
2
K
(
t
)
D
−
1
/
2
K^{(t+1)} = D^{−1/2}K^{(t)}D^{−1/2}
K(t+1)=D−1/2K(t)D−1/2,其中
D
=
d
i
a
g
(
K
(
t
)
D = diag(K^{(t)}
D=diag(K(t)1
)
)
) 和
K
(
0
)
=
K
K^{(0)} = K
K(0)=K 收敛于双随机矩阵(众所周知的“迭代比例拟合过程”的对称版本)
这个简短背景的结论是强调寻求输入亲和矩阵的双随机近似作为聚类过程的一部分的动机。悬而未决的问题是,在何种误差测量下,近似会发生?不难证明,在相对熵度量下,重复N-cuts归一化收敛于全局最优(见附录)。注意到谱聚类优化了Frobenius范数,用归一化步骤优化相对熵误差度量似乎不太自然。
本文将推导L1范数和Frobenius范数下的归一化。L1范数的目的是表明所得到的方案等同于Ratio-cut聚类——因此不引入新的聚类方案,而只是有助于统一和更好地理解N-cuts和Ratio-cut之间的差异。Frobenius范数归一化是一种基于简单迭代格式的新表述。结果归一化提供了一种新的聚类性能,在我们进行的许多标准化测试中,这种性能被证明是非常实用的,并且提高了聚类性能。
3 Ratio-cut and the L1 Normalization
假设我们希望找到输入亲和矩阵K的双重随机近似 K ′ K' K′ ,我们从L1范数近似开始:
命题1(Ratio-cut) 在L1误差范数下最接近的双随机矩阵
K
′
K'
K′ 为
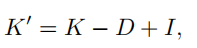
这就产生了Ratio-cut聚类算法,即将数据集划分为两个类,由拉普拉斯
L
=
D
−
K
L = D−K
L=D−K 的第二小特征向量确定,其中
D
=
d
i
a
g
(
K
D = diag(K
D=diag(K1
)
)
)。
证明: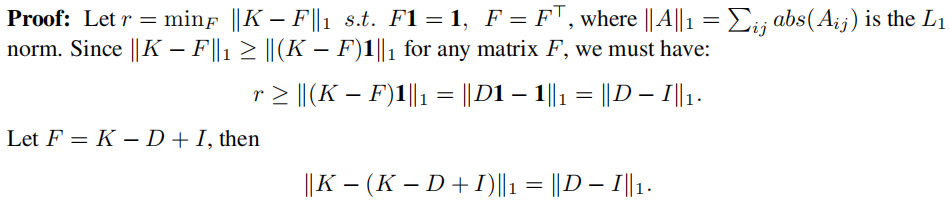
∣ ∣ ( K − F ) 1 ∣ ∣ 1 = ∣ ∣ K 1 − F 1 ∣ ∣ 1 = ∣ ∣ d i a g ( D ) − 1 ∣ ∣ = ∣ ∣ D 1 − 1 ∣ ∣ 1 ||(K-F) 1 ||_1 = ||K1-F1||_1= ||diag(D)-1||=||D1-1||_1 ∣∣(K−F)1∣∣1=∣∣K1−F1∣∣1=∣∣diag(D)−1∣∣=∣∣D1−1∣∣1
如果 v 是特征值为 λ 的拉普拉斯算子 L = D − K L = D - K L=D−K 的特征向量,则 v 也是特征值为 1 - λ 的 K ′ = K − D + I K' = K - D + I K′=K−D+I 的特征向量,并且由于 ( D − K ) (D - K) (D−K)1 = 0 = 0 =0,则拉普拉斯算子的最小特征向量 v =1 是 K ′ K' K′ 的最大特征向量,并且拉普拉斯算子的第二小特征向量( Ratio-cut 结果)对应于 K ′ K' K′ 的第二大特征向量。
到目前为止,我们所知道的是,作为两种流行的谱聚类方案,N-cuts和Ratio-cuts之间的区别在于,前者使用相对熵误差度量来寻找 K K K 的双重随机近似值,而后者使用L1范数误差度量(结果是带有附加单位矩阵的负拉普拉斯)。
4 Normalizing under Frobenius Norm
鉴于谱聚类优化了Frobenius范数,有一个强有力的论据支持找到一个最优的Frobenius范数双随机近似
K
K
K。优化设置是一个二次线性规划(QLP)。然而,我们问题的特殊情况使得QLP的解决方案由一个非常简单的迭代计算组成,如下所述。
在Frobenius范数下,最接近的双随机矩阵
K
′
K'
K′ 是以下QLP的解:
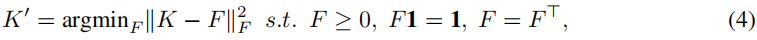
我们定义了接下来的两个子问题,每个子问题都有一个封闭形式的解,并让我们的QLP解在两个问题之间依次交替,直到收敛。考虑仿射子问题:
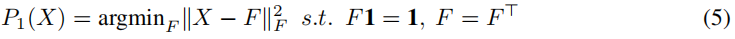
凸子问题:
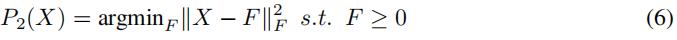
我们将使用冯-诺伊曼[5]连续投影引理,说明
P
1
P
2
P
1
P
2
…
P
1
(
K
)
P_1P_2P_1P_2…P_1(K)
P1P2P1P2…P1(K)将收敛于
K
K
K 在上述仿射子空间和二次子空间交点上的投影。因此,需要证明的是,投影
P
1
P_1
P1 和
P
2
P_2
P2 可以有效地求解(并且以封闭形式)。
我们从
P
1
P_1
P1 的解开始。对应于公式5 的拉格朗日,采取形式:
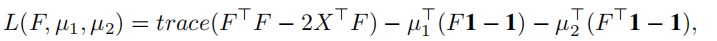
s
.
t
F
=
F
T
s.t F = F^T
s.tF=FT,我们有
µ
1
=
µ
2
=
µ
µ_1=µ_2=µ
µ1=µ2=µ。
∣ ∣ X − F ∣ ∣ F 2 = t r a c e ( ( X − F ) T ( X − F ) ) = t r a c e ( ( X T − F T ) ( X − F ) ) = t r a c e ( X T X − X T F − F T X + F T F ) = t r a c e ( X T X − 2 X T F + F T F ) ||X-F||_F^2 = trace((X-F)^T(X-F)) = trace((X^T-F^T)(X-F))=trace(X^TX-X^TF-F^TX+F^TF)=trace(X^TX-2X^TF+F^TF) ∣∣X−F∣∣F2=trace((X−F)T(X−F))=trace((XT−FT)(X−F))=trace(XTX−XTF−FTX+FTF)=trace(XTX−2XTF+FTF)
用到的性质:
∣ ∣ A ∣ ∣ F 2 = < A , A > = t r a c e ( A T A ) ||A||_F^2 = <A,A> = trace(A^TA) ∣∣A∣∣F2=<A,A>=trace(ATA)
t r a c e ( A T B ) = t r a c e ( B T A ) trace(A^TB)=trace(B^TA) trace(ATB)=trace(BTA)
t r a c e ( A + B ) = t r a c e ( A ) + t r a c e ( B ) trace(A+B) = trace(A)+trace(B) trace(A+B)=trace(A)+trace(B)
将关于F的导数设置为0:
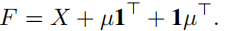
对拉格朗日函数 L ( F , μ 1 , μ 2 ) = t r a c e ( X T X − 2 X T F + F T F ) − μ 1 T ( F 1 − 1 ) − μ 2 T ( F T 1 − 1 ) L(F,\mu_1,\mu_2) = trace(X^TX-2X^TF+F^TF)-\mu_1^T(F1-1)-\mu_2^T(F^T1-1) L(F,μ1,μ2)=trace(XTX−2XTF+FTF)−μ1T(F1−1)−μ2T(FT1−1) 的 F F F求导
L = t r a c e ( X T X ) − 2 t r a c e ( X T F ) + t r a c e ( F T F ) − μ 1 T ( F 1 − 1 ) − μ 2 T ( F T 1 − 1 ) L=trace(X^TX)-2trace(X^TF)+trace(F^TF)-\mu_1^T(F1-1)-\mu_2^T(F^T1-1) L=trace(XTX)−2trace(XTF)+trace(FTF)−μ1T(F1−1)−μ2T(FT1−1)
L ′ = 2 X − 2 F − μ 1 1 T − 1 μ 2 T L'=2X-2F-\mu_11^T-1\mu_2^T L′=2X−2F−μ11T−1μ2T,令导数等0得
F = X + μ 1 T + 1 μ T F=X+\mu1^T+1\mu^T F=X+μ1T+1μT
用到的公式:
∇ t r a c e ( X T X ) = 2 X \nabla trace(X^TX)=2X ∇trace(XTX)=2X
∇ t r a c e ( A T X ) = ∇ t r a c e ( A X T ) = A \nabla trace(A^TX)=\nabla trace(AX^T)=A ∇trace(ATX)=∇trace(AXT)=A
∇ t r a c e ( A X ) = ∇ t r a c e ( A X ) = A T \nabla trace(AX)=\nabla trace(AX)=A^T ∇trace(AX)=∇trace(AX)=AT
∂ a T X T b ∂ X = b a T \frac{\partial a^TX^Tb}{\partial X} =ba^T ∂X∂aTXTb=baT
∂ a T X b ∂ X = a b T \frac{\partial a^TXb}{\partial X} =ab^T ∂X∂aTXb=abT
通过在两侧乘以1来分离
µ
µ
µ:
µ
=
(
n
I
+
µ=(nI +
µ=(nI+ 11
T
)
−
1
(
I
−
X
)
^T)^{−1}(I−X)
T)−1(I−X) 1。注意到
(
(
n
I
+
((nI +
((nI+ 11
T
)
−
1
=
(
1
/
n
)
(
I
−
(
1
/
2
n
)
^T)^{−1}=(1/n)(I−(1/2n)
T)−1=(1/n)(I−(1/2n) 11
T
)
^T)
T),我们得到了一个封闭形式的解:
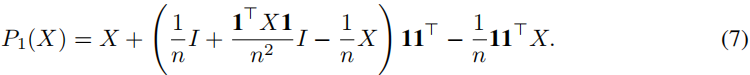
F = X + μ 1 T + 1 μ T F=X + \mu 1^T+ 1\mu^T F=X+μ1T+1μT等式两边右乘 1
⇔ 1 = X 1 + μ 1 T 1 + 1 μ T 1 \Leftrightarrow 1=X1 +\mu 1^T1+1\mu^T1 ⇔1=X1+μ1T1+1μT1
⇔ 1 = X 1 + n μ + 1 1 T μ \Leftrightarrow 1=X1 +n\mu +11^T \mu ⇔1=X1+nμ+11Tμ
⇔ ( n I + 1 1 T ) μ = ( I − X ) 1 \Leftrightarrow (nI+11^T)\mu=(I-X)1 ⇔(nI+11T)μ=(I−X)1
注:
1 T 1 = n 1^T1 = n 1T1=n
1 1 T = o n e s ( n ) 11^T=ones(n) 11T=ones(n)
1 μ T 1 = 1 1 T μ 1\mu^T1=11^T\mu 1μT1=11Tμ
投影P2(X)也可以用一种简单的封闭形式来描述。设
I
+
I_+
I+ 为对应于X的非负项的指数集,
I
−
I_-
I−为X的负项集合。准则函数
∣
∣
X
−
F
∣
∣
F
2
||X−F||^2_F
∣∣X−F∣∣F2为:
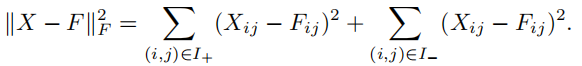
显然,对于所有
(
i
,
j
)
∈
I
+
(i, j)∈I_+
(i,j)∈I+,当
F
i
j
=
X
i
j
F_{ij} = X_{ij}
Fij=Xij时,
F
≥
0
F≥0
F≥0上的能量最小,否则为零。令
t
h
≥
0
(
X
)
th_{≥0}(X)
th≥0(X) 表示将X的所有负项归零的算子,则
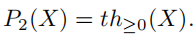
综上所述,通过重复以下步骤,可以得到将Frobenius误差范数中最接近的双随机矩阵K’返回到输入亲和矩阵K的方程4的全局最优:

参考文献:
矩阵求导公式的数学推导(矩阵求导——基础篇) - Iterator的文章 - 知乎
什么是矩阵导数及其求解方法详解 - 极速BigStone的文章 - 知乎
迹的性质
矩阵微分系列二:矩阵迹求导
矩阵F范数的平方转化为矩阵的迹






















 482
482











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








