value_based RL学习记录

最新推荐文章于 2024-02-05 15:48:21 发布

乐观的Zqq

最新推荐文章于 2024-02-05 15:48:21 发布

阅读量481

点赞数

分类专栏： deep_learing

本文链接：https://blog.csdn.net/qq_34326845/article/details/89891808

版权

deep_learing 专栏收录该内容

6 篇文章 1 订阅

订阅专栏

强化学习

使用强化学习能够让机器学着如何在环境中拿到高分, 表现出优秀的成绩. 而这些成绩背后却是他所付出的辛苦劳动, 不断的试错, 不断地尝试, 累积经验, 学习经验.
根据行为来打分，不会告诉你该怎么做，而是给这个行为打分。
下一次决策的时候记住那些可以得到高分的行为，进行这个行为，拿高分避免低分。

å¼ºåŒ–å¦ä¹ (Reinforcement Learning)

RL算法们

å¼ºåŒ–å¦ä¹ (Reinforcement Learning)

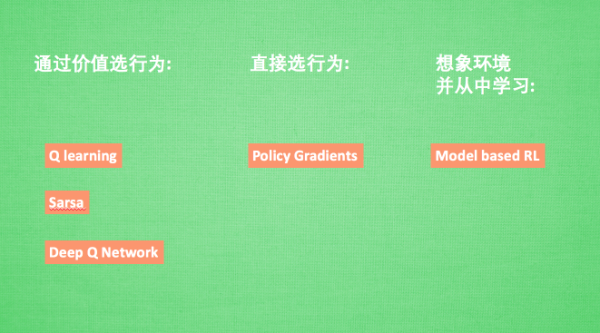
方法

不理解环境 model-free

根据真实世界的反馈，一步一步行动
Q-learning
Sarsa
Policy Gradients

理解环境 model-based

根据想象来预判下一步的行动，选择想象中最好的那一种

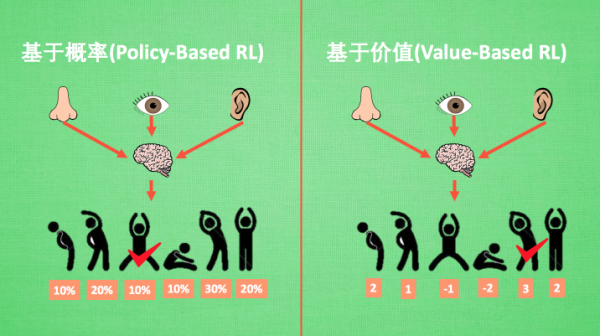
基于概率

根据计算的概率来采取行动，每一种都可能被选中，只是可能性大小的不同
Policy Gradients
连续的动作

基于价值

根据所有动作的价值，根据价值最高的行动
Q learning
Sarsa
离散的动作

å¼ºåŒ–å¦ä¹ æ–¹æ³•æ±‡æ€» (Reinforcement Learning)

回合更新

游戏开始-结束之后
基础Policy Gradients
Monte-Carlo Learning

å¼ºåŒ–å¦ä¹ æ–¹æ³•æ±‡æ€» (Reinforcement Learning)

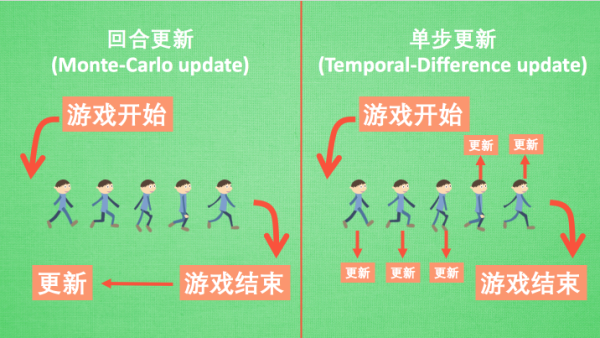
单步更新

Q-learning
Sarsa
升级版Policy Gradients

在线学习

本人边玩边学习
sarsa
sara( $\lambda$ )

离线学习

自己玩或者看着别人玩，别人的经历也可以，不用边玩别学习
Q-learning

Q-learning

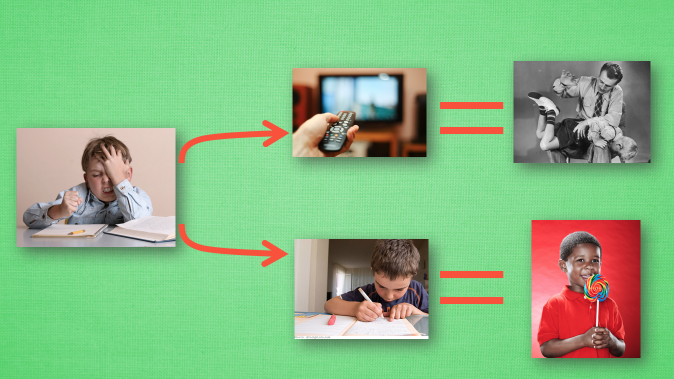
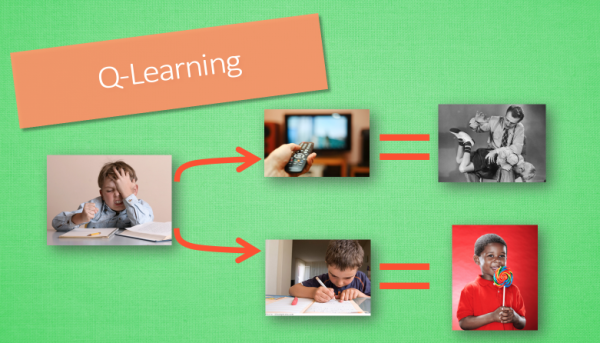
1.1行为准则

做作业和看电视的抉择

Q Leaning

1.2 Q-learning 决策

选择reward大的action

Q Leaning

1.3 Q-learning更新

Q-table怎么更新？

Q Leaning

1.4 Q-learning 整体算法

贪婪的Q-learning

Q Leaning

决策过程，根据reward来进行行为决策
会存在一个Q-table来存储不同状态下做不同行为的值，根据这个值来判断在某个状态下选择什么行为
记录行为值的方法，每种在一定状态下的行为都会有一个值Q(S,A),也就是说行为A在状态S下的值为Q(S,A)
进行决策的时候会选择**Q(S,A1)>Q(S,A2)**的时候的行为A1，再根据现实和估计值来更新Q(S,A1)
整个算法就是不断的更新Q-table中的值，根据新的值来判断在某个state采取什么样的action。
为了避免总是进行同一种决策，采用epsilon来控制是否贪婪决策。例如：epsilon=0.9，就是有90%的机会贪婪，10%的机会完全随机选择行为。
Q-learning是一个off-policy的算法（离线），因为里面的max action可以让Q-table更新不是正在经历的经验。

1.5 Q-learning中的Gamma

Gamma对于Q-learning的影响
眼睛度数-眼前的利益和未来的利益

Q Leaning

1.6 小例子-找宝藏(Q-learning)

三个py文件
main.py 主函数

#main.py

from maze_env import Maze
from RL_brain import QLearningTable
def update():
    # 学习 100 回合
    for episode in range(100):
        # 初始化 state 的观测值
        observation = env.reset()

        while True:
            # 更新可视化环境
            env.render()

            # RL 大脑根据 state 的观测值挑选 action
            action = RL.choose_action(str(observation))

            # 探索者在环境中实施这个 action, 并得到环境返回的下一个 state 观测值, reward 和 done (是否是掉下地狱或者升上天堂)
            observation_, reward, done = env.step(action)

            # RL 从这个序列 (state, action, reward, state_) 中学习
            RL.learn(str(observation), action, reward, str(observation_))

            # 将下一个 state 的值传到下一次循环
            observation = observation_

            # 如果掉下地狱或者升上天堂, 这回合就结束了
            if done:
                break

    # 结束游戏并关闭窗口
    print('game over')
    env.destroy()

if __name__ == "__main__":
    # 定义环境 env 和 RL 方式
    env = Maze()
    RL = QLearningTable(actions=list(range(env.n_actions)))

    # 开始可视化环境 env
    env.after(100, update)
    env.mainloop()

RL_brain.py 强化学习的决策部分
初始部分，功能

class QLearningTable:
    # 初始化
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):

    # 选行为
    def choose_action(self, observation):

    # 学习更新参数 
    #s:当前state 
    #a:action
    #r:reward:
    #s_:next state
    def learn(self, s, a, r, s_):

    # 检测 state 是否存在
    def check_state_exist(self, state):

完整部分

import numpy as np
import pandas as pd
class QLearningTable:
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        # a list
        self.actions = actions  
        # 学习率
        self.lr = learning_rate 
        # 奖励衰减
        self.gamma = reward_decay  
        # 贪婪度
        self.epsilon = e_greedy 
        #初始 q_table
        self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64)
    def choose_action(self, observation):
        #检测本state是否在q_table中存在
        self.check_state_exist(observation) 
        # 选择 action
        if np.random.uniform() < self.epsilon: 
             # 选择 Q value 最高的 action
            state_action = self.q_table.loc[observation, :]
            # 同一个 state, 可能会有多个相同的 Q action value, 所以我们乱序一下
            action = np.random.choice(state_action[state_action == np.max(state_action)].index)
        # 随机选择 action
        else:  
            action = np.random.choice(self.actions)

        return action
    def learn(self, s, a, r, s_):
        # 检测 q_table 中是否存在 s_ 
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        # 下个 state 不是 终止符
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, :].max()  # next state is not terminal
        else:
        # 下个 state 是终止符
            q_target = r  # next state is terminal
        # 更新对应的 state-action 值
        self.q_table.loc[s, a] += self.lr * (q_target - q_predict)  

    def check_state_exist(self, state):
        if state not in self.q_table.index:
            # append new state to q table
            self.q_table = self.q_table.append(
                pd.Series(
                    [0]*len(self.actions),
                    index=self.q_table.columns,
                    name=state,
                )
            )

maze_env.py 环境（见文件maze.env.py）

Sarsa

2.1 学习还是看电视？

Sarsa

2.2 Sarsa决策

和Q-learning类似

Sarsa

2.3 Sarsa更新准则

Sarsa的Q-table更新方式

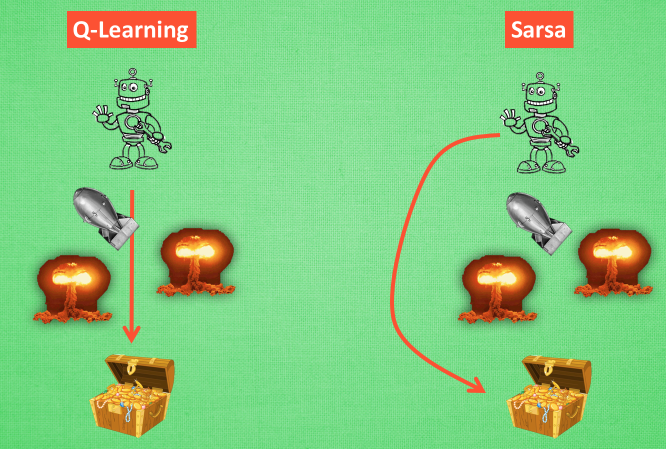
Sarsa

2.4 Sarsa和Q-learning对比

勇敢的Q-learning 和谨慎的Sarsa

Sarsa

整个算法和Q-learning一样，不断的更新Q-table的值，然后再根据新的值来判断在某个state采取怎么样的action。
不同Q-learning的是，更新Q-table方式不一样。
Q-learning是估计，Sarsa是说到做到
当Sarsa 和 Q-Learning处在状态s时，均选择可带来最大回报的动作a，这样可到达状态s’。而在下一步，如果使用Q-Learning， 则会观察在s’上哪个动作会带来最大回报（不会真正执行该动作，仅用来更新Q表），在s’上做决定时, 再基于更新后的Q表选择动作。而 Sarsa 是实践派，在**s’ 这一步估算的动作也是接下来要执行的动作，所以 Q(s, a) 的现实值也会稍稍改动，去掉maxQ，**取而代之的是在s’ 上实实在在选取的a’ 的Q值，最后像Q-Learning一样求出现实和估计的差距并更新Q表里的Q(s, a)。
Sarsa在当前state已经想好了state对应的action，而且还想好了下一个state_和下一个action_(Q-learning没有想好下一个，只能是知道根据当前的值选择的action
更新Q（s,a)的时候，Sarsa是基于下一个Q(s_,a_),(Q-learning是基于maxQ(s_)
Q-learning永远选择最好的，Sarsa选择最保险的（胆小的sarsa）;可以认为Q-learning是一种更加贪婪的方法，不考虑其他的非maxQ的结果。我们理解Q-learning是一种贪婪、大胆勇敢的算法，不考虑错误，不考虑死亡。而Sarsa是一种保守，敏感的算法，对于每一步的决策，都处于一种远离危险的状态。
只能从自身的经验学习
Q learning 机器人永远都会选择最近的一条通往成功的道路, 不管这条路会有多危险. 而 Sarsa 则是相当保守, 他会选择离危险远远的, 拿到宝藏是次要的, 保住自己的小命才是王道.

Sarsa

2.5 小例子-找宝藏(Sarsa)

from maze_env import Maze
from RL_brain import SarsaTable
def update():
    for episode in range(100):
        # 初始化环境
        observation = env.reset()
        # Sarsa 根据 state 观测选择行为
        action = RL.choose_action(str(observation))
        while True:
            # 刷新环境
            env.render()
            # 在环境中采取行为, 获得下一个 state_ (obervation_), reward, 和是否终止
            observation_, reward, done = env.step(action)
            # 根据下一个 state (obervation_) 选取下一个 action_
            action_ = RL.choose_action(str(observation_))
            # 从 (s, a, r, s, a) 中学习, 更新 Q_tabel 的参数 ==> Sarsa
            RL.learn(str(observation), action, reward, str(observation_), action_)
            # 将下一个当成下一步的 state (observation) and action
            observation = observation_
            action = action_
            # 终止时跳出循环
            if done:
                break
    # 大循环完毕
    print('game over')
    env.destroy()
if __name__ == "__main__":
    env = Maze()
    RL = SarsaTable(actions=list(range(env.n_actions)))
    env.after(100, update)
    env.mainloop()

Sarsa主结构

import numpy as np
import pandas as pd

class RL(object):
    def __init__(self, action_space, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        ... # 和 QLearningTable 中的代码一样

    def check_state_exist(self, state):
        ... # 和 QLearningTable 中的代码一样

    def choose_action(self, observation):
        ... # 和 QLearningTable 中的代码一样

    def learn(self, *args):
        pass # 每种的都有点不同, 所以用 pass
    
class QLearningTable(RL):   # 继承了父类 RL
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        super(QLearningTable, self).__init__(actions, learning_rate, reward_decay, e_greedy)    # 表示继承关系

    def learn(self, s, a, r, s_):   # learn 的方法在每种类型中有不一样, 需重新定义
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, :].max()
        else:
            q_target = r
        self.q_table.loc[s, a] += self.lr * (q_target - q_predict)
        
class SarsaTable(RL):   # 继承 RL class

    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        super(SarsaTable, self).__init__(actions, learning_rate, reward_decay, e_greedy)    # 表示继承关系

    def learn(self, s, a, r, s_, a_):
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            # q_target 基于选好的 a_ 而不是 Q(s_) 的最大值
            q_target = r + self.gamma * self.q_table.loc[s_, a_]  
        else:
            q_target = r  # 如果 s_ 是终止符
        # 更新 q_table
        self.q_table.loc[s, a] += self.lr * (q_target - q_predict)

Sarsa（ $\lambda$ ）

Sarsa的更新版本
单步更新，之后获得reward后才会更新（只有获得宝藏时，才会更新获得宝藏的上一步，这一步和获得宝藏有关系），之前为了获得宝藏走的所有步都被认为和宝藏没有关系的，
回合更新，虽然是到了回合的结尾才会更新，所有步都进行更新，都是有关系的，所以这些步在下一回合的概率更大了一些。
$\lambda$ 是一个衰变值
取0 单步更新
去1 回合更新
0-1之间，越大和宝藏越近的地方更新越大。这样我们就不用受限于单步更新的每次只能更新最近的一步, 我们可以更有效率的更新所有相关步了.

DQN(Deep Q Network)

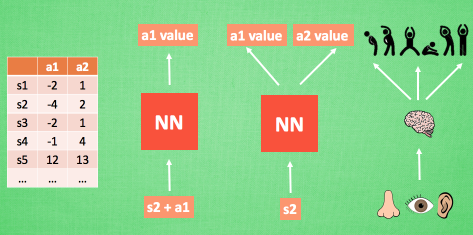
3.1 神经网络

DQN

由来：传统的表格形式强化学习有一个瓶颈，使用表格存储每一个state和在这个state每个action对应的Q值。例如：围棋，一个19*19=361个子，空间复杂度约等于 $10^{93}$ 而宇宙中总原子的数量才10^{80}个
缺点：在当今问题太复杂的情况下不能胜任，因为状态太多，例如围棋棋盘的状态
解决方法：
- 1.利用神经网络来处理输入的状态（状态和动作），从而得到一个Q值
- 2.输入状态，输出所有动作值，然后根据Q-learning的贪婪原则，选择值最大的动作。

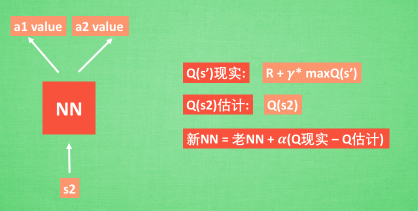
3.2 更新神经网络

基于第二种神经网络
Q现实：Q-learning中的Q-table的值
Q估计：神经网络得到的

DQN

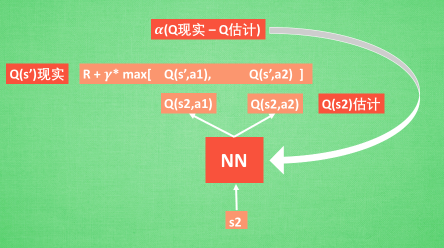
3.3 Experience replay

记忆库（重复学习)
所以每次 DQN 更新的时候, 我们都可以随机抽取一些之前的经历进行学习. 随机抽取这种做法打乱了经历之间的相关性, 也使得神经网络更新更有效率

DQN

3.4 Fixed Q-targets

冻结参数，切断相关性
也是一种打乱相关性的机理, 如果使用 fixed Q-targets, 我们就会在 DQN 中使用到两个结构相同但参数不同的神经网络, 预测 Q 估计的神经网络具备最新的参数, 而预测 Q 现实的神经网络使用的参数则是很久以前的.

3.5 DQN算法详解

在Q-learing的基础上加了一些装饰
1.记忆库
2.利用神经网络计算Q值(而不是Q-table).‘
- 两个结构相同的神经网络分别计算Q现实和Q估计。
- 每隔C步进行Q现实和Q估计的更新

1555831429347

3.6 小例子-找宝藏(DQN)

两个结构相同但参数不同的神经网络，Q现实和Q估计
DQN_modified.py部分代码 _build_net()

def _build_net(self):
        # ------------------ all inputs ------------------------
        self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s')  # input State
        self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_')  # input Next State
        self.r = tf.placeholder(tf.float32, [None, ], name='r')  # input Reward
        self.a = tf.placeholder(tf.int32, [None, ], name='a')  # input Action

        w_initializer, b_initializer = tf.random_normal_initializer(0., 0.3), tf.constant_initializer(0.1)

        # ------------------ build evaluate_net ------------------
        with tf.variable_scope('eval_net'):
            e1 = tf.layers.dense(self.s, 20, tf.nn.relu, kernel_initializer=w_initializer,
                                 bias_initializer=b_initializer, name='e1')
            self.q_eval = tf.layers.dense(e1, self.n_actions, kernel_initializer=w_initializer,
                                          bias_initializer=b_initializer, name='q')

        # ------------------ build target_net ------------------
        with tf.variable_scope('target_net'):
            t1 = tf.layers.dense(self.s_, 20, tf.nn.relu, kernel_initializer=w_initializer,
                                 bias_initializer=b_initializer, name='t1')
            self.q_next = tf.layers.dense(t1, self.n_actions, kernel_initializer=w_initializer,
                                          bias_initializer=b_initializer, name='t2')

        with tf.variable_scope('q_target'):
            q_target = self.r + self.gamma * tf.reduce_max(self.q_next, axis=1, name='Qmax_s_')    # shape=(None, )
            self.q_target = tf.stop_gradient(q_target)
        with tf.variable_scope('q_eval'):
            a_indices = tf.stack([tf.range(tf.shape(self.a)[0], dtype=tf.int32), self.a], axis=1)
            self.q_eval_wrt_a = tf.gather_nd(params=self.q_eval, indices=a_indices)    # shape=(None, )
        with tf.variable_scope('loss'):
            self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval_wrt_a, name='TD_error'))
        with tf.variable_scope('train'):
            self._train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)

学习部分

    def learn(self):
        # check to replace target parameters
        if self.learn_step_counter % self.replace_target_iter == 0:
            self.sess.run(self.target_replace_op)
            print('\ntarget_params_replaced\n')

        # sample batch memory from all memory
        if self.memory_counter > self.memory_size:
            sample_index = np.random.choice(self.memory_size, size=self.batch_size)
        else:
            sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
        batch_memory = self.memory[sample_index, :]

        _, cost = self.sess.run(
            [self._train_op, self.loss],
            feed_dict={
                self.s: batch_memory[:, :self.n_features],
                self.a: batch_memory[:, self.n_features],
                self.r: batch_memory[:, self.n_features + 1],
                self.s_: batch_memory[:, -self.n_features:],
            })

        self.cost_his.append(cost)

        # increasing epsilon
        self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_max
        self.learn_step_counter += 1

主函数部分

def run_maze():
    step = 0    # 用来控制什么时候学习
    for episode in range(300):
        # 初始化环境
        observation = env.reset()
        while True:
            # 刷新环境
            env.render()
            # DQN 根据观测值选择行为
            action = RL.choose_action(observation)
            # 环境根据行为给出下一个 state, reward, 是否终止
            observation_, reward, done = env.step(action)
            # DQN 存储记忆
            RL.store_transition(observation, action, reward, observation_)
            # 控制学习起始时间和频率 (先累积一些记忆再开始学习)
            if (step > 200) and (step % 5 == 0):
                RL.learn()
            # 将下一个 state_ 变为 下次循环的 state
            observation = observation_
            # 如果终止, 就跳出循环
            if done:
                break
            step += 1   # 总步数
    # end of game
    print('game over')
    env.destroy()
if __name__ == "__main__":
    env = Maze()
    RL = DeepQNetwork(env.n_actions, env.n_features,
                      learning_rate=0.01,
                      reward_decay=0.9,
                      e_greedy=0.9,
                      replace_target_iter=200,  # 每 200 步替换一次 target_net 的参数
                      memory_size=2000, # 记忆上限
                      # output_graph=True   # 是否输出 tensorboard 文件
                      )
    env.after(100, run_maze)
    env.mainloop()
    RL.plot_cost()  # 观看神经网络的误差曲线