图深度学习——复杂图嵌入:异质图，二分图，多维图，超图，符号图，动态图

复杂图嵌入

复杂图更适合于现实的应用

大部分针对复杂图设计的方法和针对简单图的算法是相似的。

复杂图简介

异质图

异质图除了边和节点的集合外，还包含两个映射函数。因为在异质图中，节点和边的种类是有不同的，这个映射函数就是将节点和边映射到他们的类型上去。

在上图的例子中，有三种类型的节点和三种类型的边。在异质图上做嵌入，和在简单图中做嵌入最本质的区别就是，如何针对异质图来设计不同的游走方法（在DeepWalk中的随机游走）

Meta-Path模式

• mate-path不是一种路径，而是一种随机游走的模式
• 不同的meta-path模式捕捉不同的语义信息
• meta-path模式一般需要利用专业知识来预先定义好
• 定义不同的meta-path模式可以进行不同的随机游走，产生不同的途径

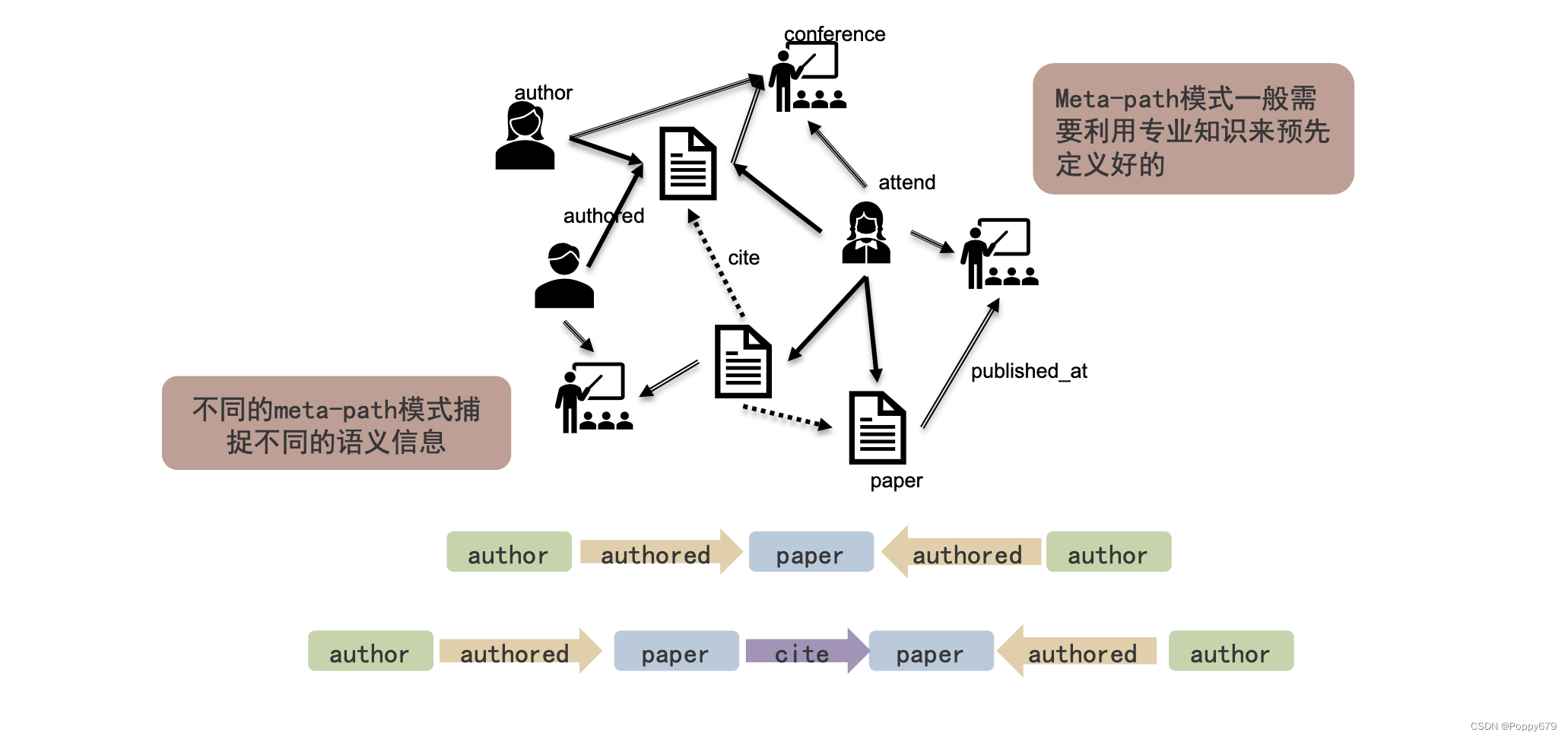
怎么去发现meta-path模式？需要通过预先定义或自动挖掘方法

meta-path 就定义了图上的随机游走方式。进行随机游走必须符合meta-path定义的模式

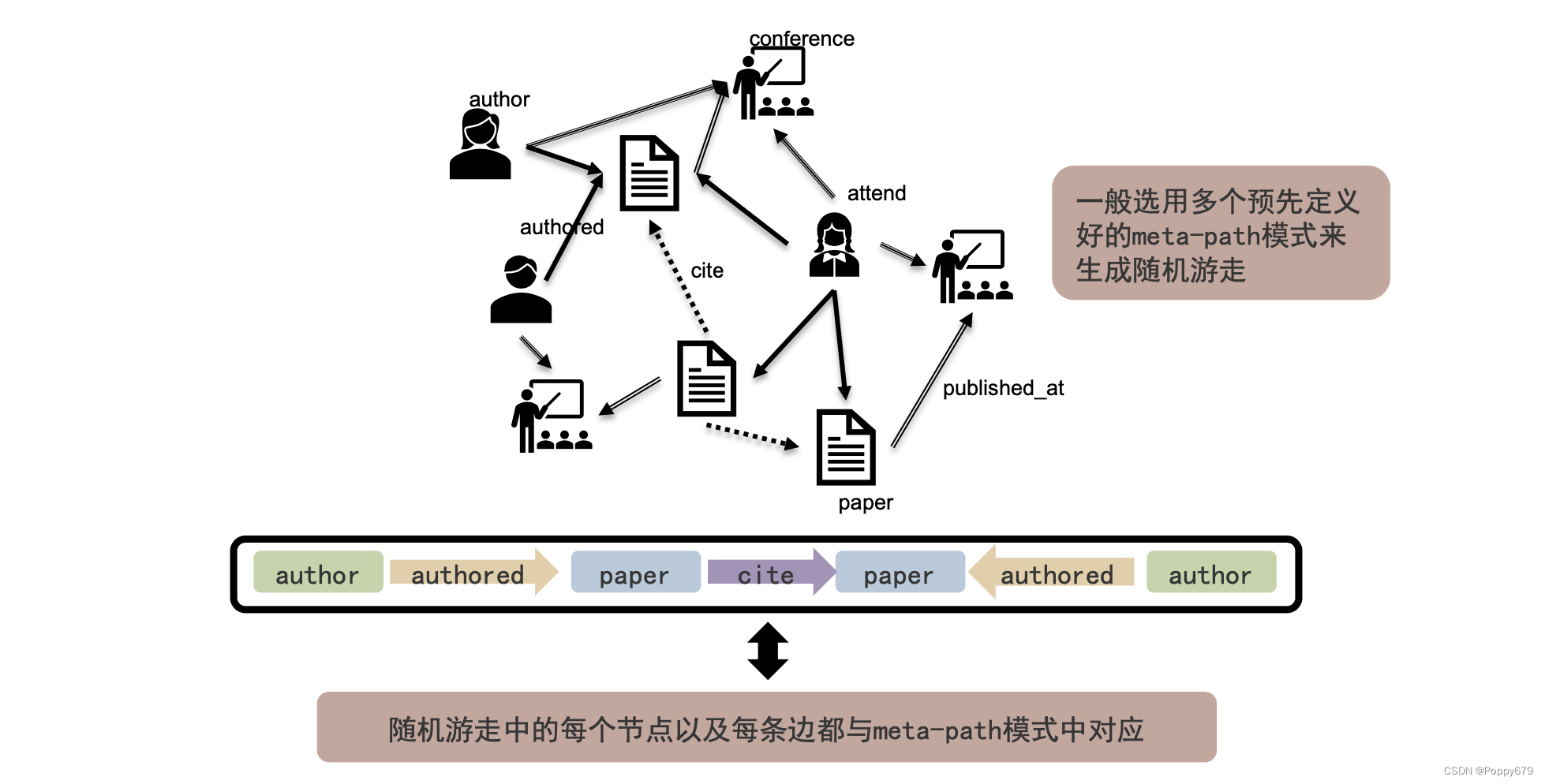
基于Meta-Path的随机游走

一般选用多个预先定义好的Meta-path模式来生成随机游走，这样可以产生一系列随机游走序列。

异质图嵌入：metapath2vec

基于metapath 的随机游走产生序列，再与DeepWalk相同的处理方法来进行图嵌入操作。

二分图

二分图的节点被分为两个不相交的子集，每一个子集内没有边。

信息提取器

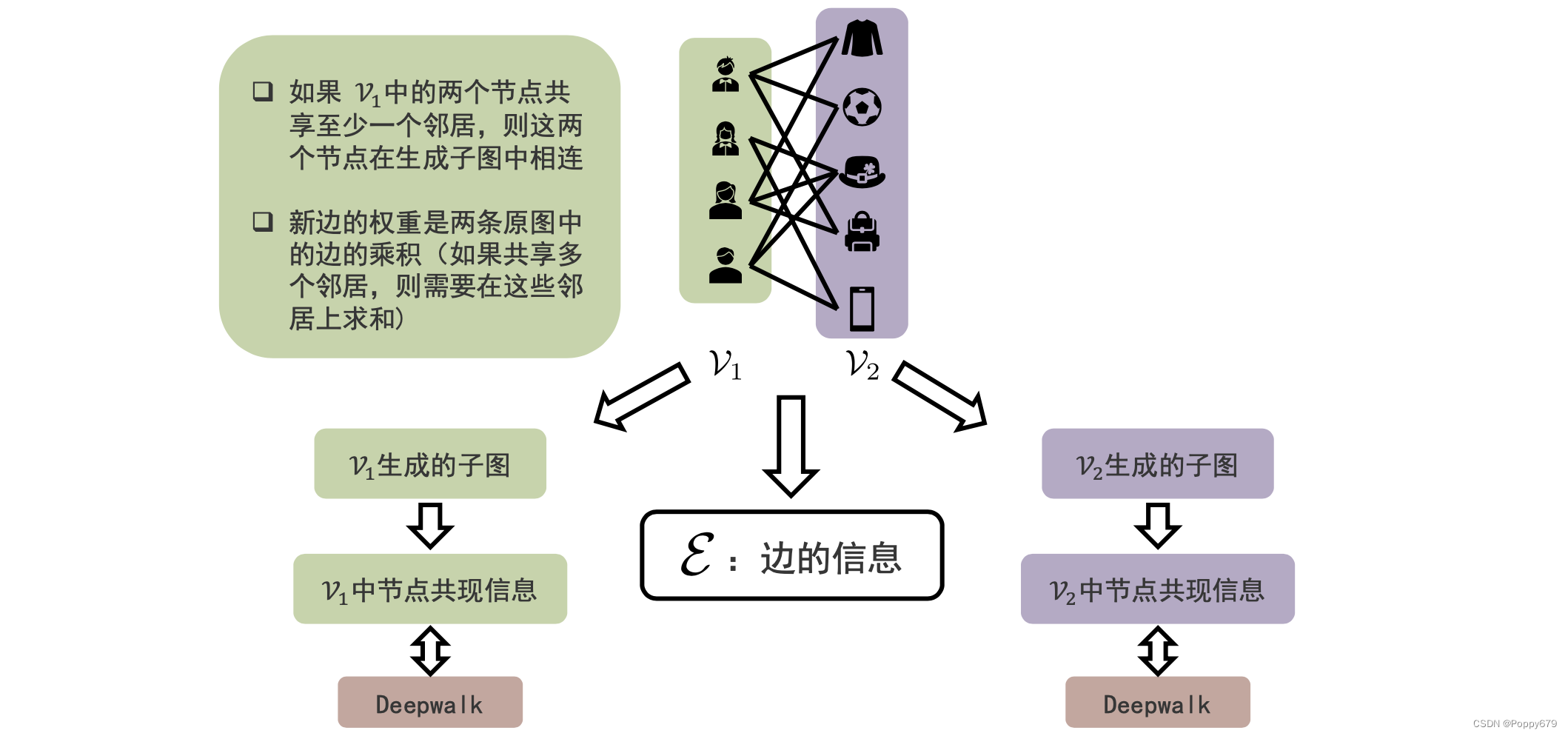
二分图的信息提取器有三种：

• 基于边的信息
• 通过二分图生成关于节点集合1的子图
• 通过二分图生成关于节点集合2的子图

信息提取的一些原则/方法：

1. 如果 $V_1$ 中的两个节点共享至少一个邻居，则这两个节点在生成子图中相连
   一些小想法：在网络入侵检测中，如果两个源ip的目标ip是同一个，那么他们的关系可以在信息提取中成为相连的邻居；或者如果样本使用的协议是同一个，那他们之间存在连接…
2. 新边的权重是两条原图中的边的乘积（如果共享多个邻居，则需要在这些邻居上求和）

通过生成两类节点的简单图，就可以从中提取各自的共现信息，再通过DeepWalk就可以得到各自简单图中各个节点的嵌入表示。

边的信息的重构器和目标函数

边的表示：$e=\left(v^{(1)},v^{(2)}\right)$，在重构器中就是通过给定两个节点去预测是否存在边：$p\left(e\mid v^{(1)},v^{(2)}\right)$，使这个存在边的概率最大化。对概率建模的方式是通过相似性（sigmoid函数？逻辑回归？）：

$p\left(e\mid v^{(1)},v^{(2)}\right)=\sigma \left(f{\left(v^{(1)}\right)}^{\top }f\left(v^{(2)}\right)\right)$

考虑所有边的概率，公式表示：

${\prod }_{e\in \mathcal{E}}p\left(e\mid v^{(1)},v^{(2)}\right)={\prod }_{e\in \mathcal{E}}\sigma \left(f{\left(v^{(1)}\right)}^{\top }f\left(v^{(2)}\right)\right)$

抽取的信息和重构信息尽可能接近，即，重构边的信息尽可能预测正确观察到的边的信息（共现信息），就是要对所有边重构的概率最大化，通常是最小化上式的对数的相反数。

多维图

同一对节点之间可以同时存在多种不同的关系

又一些小想法：网络中的访问、请求和数据交互是否也可以以多维图的形式表示？

多维图和异质图差别： 多维图上的节点之间同时存在多种不同的关系，异质图虽然也存在多种不同的边，但是在其中的节点之间只会存在一条边（一种关系）

多维图中有多个维度，每一个维度上的节点都是一样的（节点的集合是一样的），但是每一个维度上节点的关系是不一样的，即多个维度表示多种节点之间的关系。

多维图映射函数

对于每一个节点 $i$ 都有一个通用的映射函数，对于不同维度的节点又会有各自维度特定的映射函数。例如，在维度为3的多维图中，会存在4个映射函数，一个通用映射函数和三个不同维度的特定映射函数。

通用映射函数：捕捉各个维度共享的信息
维度特定映射函数：捕捉各个维度特有的信息

一个节点在某一维度的特定表示：

${\mathbf{u}}_i^{\text{blue }}=f\left(v_i\right)+f_{\text{blue }}\left(v_i\right)$

信息提取器

在不同维度上随机游走，得到每个维度的共现信息，在不同维度之间（层和层之间）不存在随机游走。捕捉维度共享的信息，也捕捉到维度共现的信息。

重构器和目标函数

在重构器中只需要提取每个维度的共现信息，然后利用节点在维度内的特定表示就能重构每个维度的共现信息。每一维度内的重构过程以及目标函数域DeepWalk一致。
重构过程：

目标函数：

对于一个 $k$ 维图，其中每个节点有 $k+1$ 个映射/嵌入，对于某一个特定的任务，如何选择节点的嵌入表示？如果任务是通用任务（分类）–>通用映射，如果任务是某一个维度的连接预测–> 在特定维度的映射…在实际应用中，也可以融合这些映射信息。

符号图

符号图中，边可以被分为两个不相交的子集，这两个子集分别包含正边和负边。并且正边和负边之间是没有重合的，即两个节点之间只会存在一种关系（正/负）

信息提取器

信息提取–平衡理论（社会科学的一种理论）
例如在一个教室中，有你喜欢的同学和你不喜欢的同学，通常我们会选择跟喜欢的同学坐的更近，同时远离不喜欢的同学。就是说在一个映射空间中，会接近朋友，远离敌人。在这样的空间中，针对每一个用户（节点 $v_i$ ）提取三元组。在这个三元组中 $v_i$和 $v_j$ 是一种正关系， $v_i$和 $v_k$ 是一种负关系，可以形式化的表示：

I = { ( v i , v j , v k ) ∣ A i , j = 1 , A i , k = − 1 } \mathcal{I}=\left\{\left(v_{i}, v_{j}, v_{k}\right) \mid \boldsymbol{A}_{i, j}=1, \boldsymbol{A}_{i, k}=-1\right\} I={(vi​,vj​,vk​)∣Ai,j​=1,Ai,k​=−1}

$\mathcal{I}$ 是所有这种形式的三元组的集合，符号图中会用符号邻接矩阵表示。正边是1，负边是-1，没有边为0。

重构器与目标函数

$f$ 是映射函数，$s$ 是相似度衡量函数。想要 $v_i，v_j$ 比 $v_i，v_k$ 更加相似，这里相似度用一个系数 $\delta$ 来表示，只有相似度大于这个值，才算是更加重要/相似的。因此最大化下述式子来尽可能的使正向边的节点对相似度大于负向边的节点对的相似度：

$s\left(f\left(v_i\right),f\left(v_j\right)\right)-\left(s\left(f\left(v_i\right),f\left(v_k\right)\right)+\delta \right))$

超图

超图是包含超边的图，超边可以描述超越两两之间的关系的更高维度的关系。原来的图描述的是两两节点之间的关系，在超图中描述的是多个节点与多个节点之间的关系。

信息提取器

信息提取：

1. $\mathcal{E}$：超边的信息
   给定一个超边，其代表了多个节点的信息。
2. $\mathcal{A}$: 节点在超边中的共现信息
   某个节点出现在多个超边中，它包含的超边的共现信息
   ${\mathcal{A}}_{i,j}$: 节点 $v_i$ 和 $v_j$ 在所有超边中共现的次数
   ${\mathcal{A}}_i$： $\mathcal{A}$ 的第 $i$ 行，表示节点 $v_i$ 和其他所有节点的共现情况

重构器与目标函数：超边中的共现信息

映射函数：$f\left(v_i\right)=MLP\left(A_i\right)$

其中 $\mathcal{A}$ 表示节点在超边中的共现信息。映射函数： 将每一个节点与其他节点在超边中共现的概率/频率放入一个感知机（MLP）得到一个嵌入表示（编码）。通常，将共现的概率放入一个MLP去重组共现信息（解码），就可以看作一个编码器和一个解码器。
最终目的是使得编码/解码得到的数据与原始的共现信息尽可能的接近，最小化： ${\sum }_{v_i\in \mathcal{V}}{\Vert {\mathbf{A}}_i-{\hat{\mathbf{A}}}_i\Vert }_2^2$ ，由此学习到每一个节点的嵌入信息。
这样的形式可以看作是一个自编码器。

重构器与目标函数：超边

超边信息的重构，与二分图中两种节点之间边的关系相似。对于给定的三个节点，去预测是否存在这样的使之存在联系的超边的概率。
最大化目标函数：

${\prod }_{e\in \mathcal{E}}p\left(e\mid \left\{v^{(1)},v^{(2)},v^{(3)}\right\}\right)={\prod }_{e\in \mathcal{E}}\sigma \left(MLP\left(\left[f\left(v^{(1)}\right),f\left(v^{(2)}\right),f\left(v^{(3)}\right)\right]\right)\right)$

动态图

动态图中，边和节点都有对应的时间信息。

时序随机游走

在动态图中的随机游走，不光要考虑邻域信息还要考虑时间顺序。

• 只能按时间顺序进行随机游走
• 下一条边的发生时间要在上一条边的发生时间之后

当前节点 $v_k$ 游走到下一个节点 $v_{k+1}$ 的概率：

$p\left(v^{(k+1)}\mid v^{(k)}\right)=\{\begin{array}{l}\mathrm{pre}\left(v^{(k+1)}\right),\text{ 如果边 }\left(v^{(k)},v^{(k+1)}\right)\text{ 发生在 }\left(v^{(k-1)},v^{(k)}\right)\text{ 之后 }\\ 0,\text{ 如果边 }\left(v^{(k)},v^{(k+1)}\right)\text{ 发生在 }\left(v^{(k-1)},v^{(k)}\right)\text{ 之前 }\end{array}$

如果过去已经存在边，那么现在游走过去的概率为0，因为不会向过去游走。如果节点 $k+1$ 发生在 $k$ 之后，那么就存在游走过去的概率，这与当前时间差有关（尽可能想游走到距离当前时间更近的节点/边）。

举例：从节点 $v_3$ 游走到下一个节点 $v_5$，此时从 $v_5$ 继续游走，可能到 $v_2，v_4，v_6$，但是可以看到 $v_2$ 是 $t_5$ 时刻的节点，但是 $v_3$ 到 $v_5$ 是 $t_6$ 时刻，说明 $v_2$ 是过去的节点，那么游走到 $v_2$ 的概率为0；由于节点 $v_5$ 到 $v_6$ 的时间为 $t_7$，相比 $v_5$ 到 $v_4$ 之间的时间 $t_8$ 更接近，因此游走到 $v_6$ 的概率更大。

因此可以知道，在时序随机游走中，会以较高的概率选择离当前时间具有较小间隔的节点。

动态图嵌入

首先根据时序的随机游走抽取时序共现信息，后续学习方法和DeepWalk类似，最终得到动态图嵌入表示。