图的类型理解

本文主要对图的类型（同质图、异质图和动态图）分别进行理解和介绍。

 同质图

同质图(Homogeneous Graph)可以定义为节点集合和边集合：G=(V,E)G=(V,E)，一条边(u,v)∈E(u,v)∈E表示节点uu与节点vv相连。节点和边上往往还附加有特征，我们记$xv为节点为节点v的特征，的特征，x{(u,v)}为边为边(u,v)$的特征。

包括PyG和DGL在内的许多图神经网络框架，都对同质图上的GNN进行过归纳，提出了相应的计算范式。例如，DGL把GNN的前向计算过程归纳为消息函数(message function)、聚合函数(reduce function)和更新函数(update function)[7]。

我们扩展了聚合函数的种类，提出一种更加通用的计算范式：

上述计算范式仍然分为生成消息、聚合消息、更新当前节点三个步骤，具体包括：

• 层次维度的聚合函数ρL(⋅)ρL(⋅)：用于聚合同一节点在模型不同层次的表示。例如，多数GNN模型中，层次维度的聚合函数为上一层的节点表示；而在JKNet[10]中，层次维度的聚合函数可以设定为LSTM[11]。
• 消息函数ϕ(⋅)ϕ(⋅)：结合起始节点和目标节点，以及边的特征，生成用于消息传递的消息向量。
• 节点维度的聚合函数ρN(⋅)ρN(⋅)：汇集了来自邻居节点N(v)N(v)的所有消息向量。值得注意的是，N(v)N(v)也可以有不同的实现。例如，在GCN中为所有邻居节点，而在GraphSage[9]中为邻居节点的子集。
• 更新函数ψ(⋅)ψ(⋅)：用于聚合节点自身在上一层和当前层的表示。

不难看出，上述计算范式可以覆盖当前大多数GNN模型。在工程实践中，我们将上述函数进一步分拆细化，预先提供了多种高效的实现。通过配置选项即可实现不同的组合搭配，从而实现多数主流的GNN模型。

 异质图

相比于同质图，异质图(Heterogeneous Graph)扩充了节点类型和边类型。 如下图2所示：

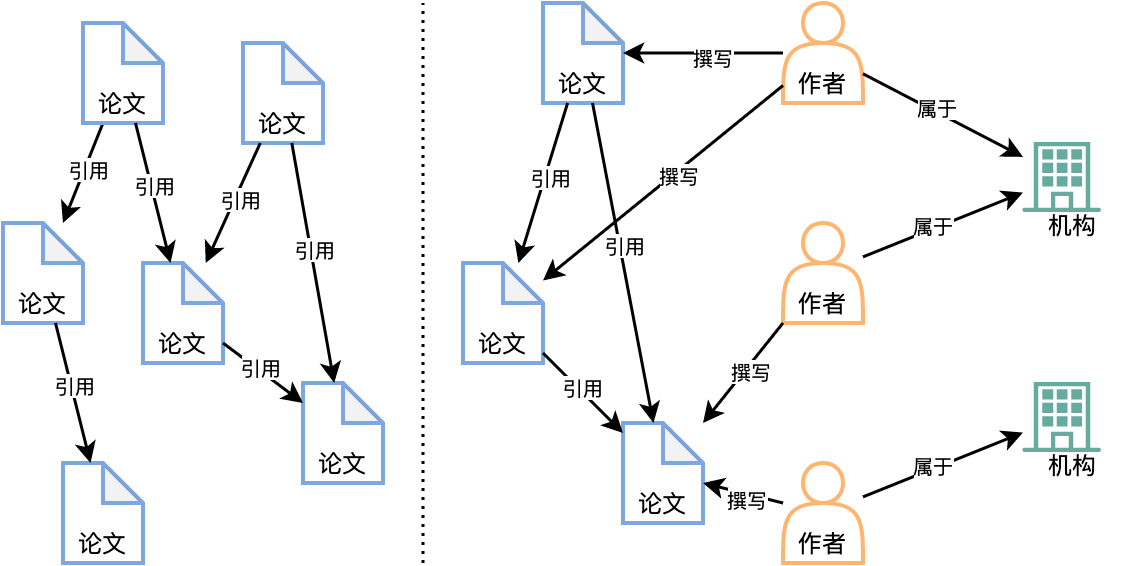
我们把异质图视为多个二分图的叠加，每一个二分图对应于一种边类型。上述的学术引用网络可以表示成“论文-引用-论文”、“作者-撰写-论文”、“作者-属于-机构”，共计三个二分图，同质图的GNN模型框架稍加修改即可在二分图上应用。

在此基础上，一个节点在不同的二分图中会产生不同的表示。我们进一步提出边类型维度的聚合函数ρR(⋅)ρR(⋅)，用于聚合节点在不同二分图中的表示（如下图3所示）。框架中同样提供边类型纬度聚合函数的多种实现，可以通过配置选项调用。例如，要实现RGCN，可以在二分图上应用GCN，然后在边类型维度上取平均。

动态图

动态图(Dynamic Graph)是指随时间变化的图。与之相对的，上述的同质图和异质图可以称为静态图。比如，学术引用网络会随时间不断扩张，用户与商品的交互图会随用户兴趣而变化。动态图上的GNN模型旨在生成给定时间下的节点表示H(t)H(t)。根据时间粒度的粗细，动态图可分为离散时间动态图和连续时间动态图。

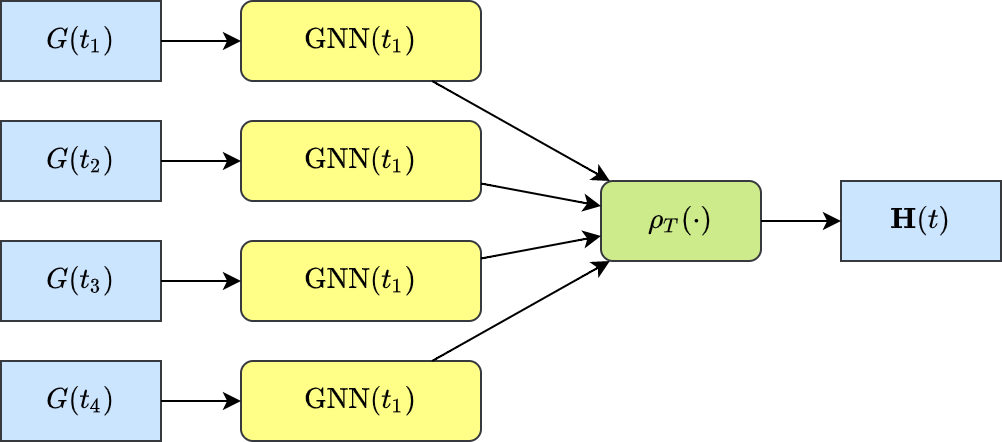
在离散时间动态图中，时间被划分为多个时间片（例如以天/小时划分），每个时间片对应一个静态的图。离散时间动态图的GNN模型通常在每个时间片上单独应用GNN模型，然后聚合节点在不同时间的表征[14]。我们把聚合过程抽象为离散时间维度的聚合函数ρT(⋅)ρT(⋅)，同样提供预定义的实现。此外，Tulong框架还提供离散时间动态图数据的加载和管理机制，仅在内存中保留必须的时间片，降低硬件资源的消耗。

在连续时间动态图中，每条边附有时间戳，表示交互事件发生的时刻。相比于静态图，连续时间动态图中的消息函数ϕ(⋅,t,et)ϕ(⋅,t,et)还依赖于给定样本的时间戳以及边的时间戳。此外，邻居节点N(v,t)N(v,t)必须与时间有关，例如邻居节点中不能出现tt时刻之后才出现的节点。针对此问题，我们开发了多种连续时间动态图上的邻居节点采样器，可以在指定的时间范围内，高效地采样邻居节点。

以上分析了同质图、异质图和动态图的计算范式，我们从中抽取出通用的函数（算子），包括消息函数、聚合函数、更新函数、邻居节点函数，并给出多种预定义的实现。框架用户通过配置选项即可拼装组合算子，从而实现需要的GNN模型。

本文来自美团的一些技术文章，仅提供学习参考