3D数学基础2：矩阵和3D线性变换

线性变换包括旋转、缩放、投影、镜像、切变等，不包括平移。包含平移的变换称作仿射变换。3D中的仿射变换不能用 $3\times 3$ 矩阵表达，只能用用 $4\times 4$ 矩阵表达仿射变换。
考虑2D 中将一物体顺时针旋转20°：旋转物体，意味着旋转物体上所有的点，这些点将被移动到一个新的位置，我们使用同一坐标系来描述变换前和变换后点的位置。如图：

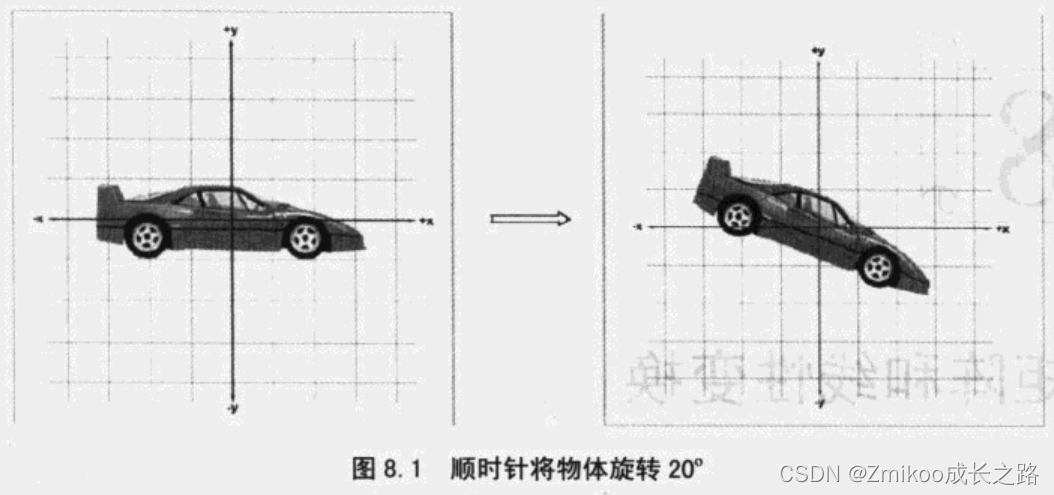
另一种方式：变换坐标系。旋转坐标系时，物体上的点实际没有移动，只是在另一个坐标系中描述它的位置而已。如图：

这两种变换实际上是等价的，将物体变换一个量等价于将坐标系变换一个相反的量。
当有多个变换时,则需要以相反的顺序变换相反的量。例如，将物体顺时针旋转20°，扩大200%,等价于将坐标系缩小200%，再逆时针旋转20°。

旋转

2D中的旋转

在2D环境中，物体只能绕某个点旋转，这里限制物体只绕原点旋转。2D中绕原点的旋转只有一个参数:角度 $\theta$，它描述了旋转量。逆时针旋转经常(不是必须)被认为是正方向，顺时针方向是负方向。下图展示了基向量 $\vec{p}$ $\vec{q}$绕原点旋转，得到新的基向量 $\vec{p}\prime$， $\vec{q}\prime$。

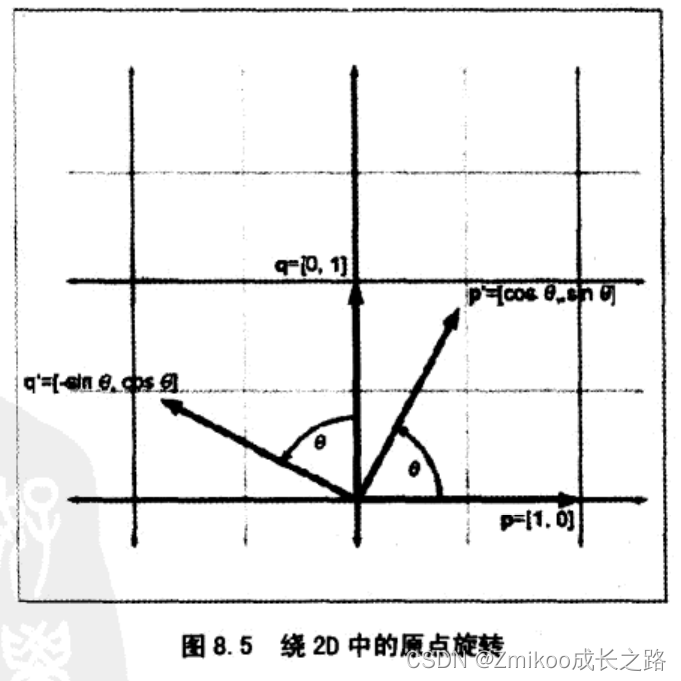
旋转后基向量的值，可以构造矩阵如下:
$R(\theta )=\left[\begin{array}{c}\vec{p}\prime \\ \vec{q}\prime \end{array}\right]=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]$

3D中的旋转

在3D场景中，绕轴旋转而不是点(此时，轴指的是旋转所绕的直线，不一定是笛卡尔坐标轴x，y或z)。由于暂不考虑平移，所以只讨论旋转轴穿过原点的情况。
绕轴旋转 $\theta °$ 时，必须知道哪个方向被认为“正”，哪个方向被认为“负”，左手坐标系中定义此方向的规则为左手法则: 伸出左手，大拇指向上，其余四指弯曲，大拇指指向旋转轴的正方向，此时四指弯曲的方向就是旋转的正方向。如果用的是右手坐标系，则使用右手法则。

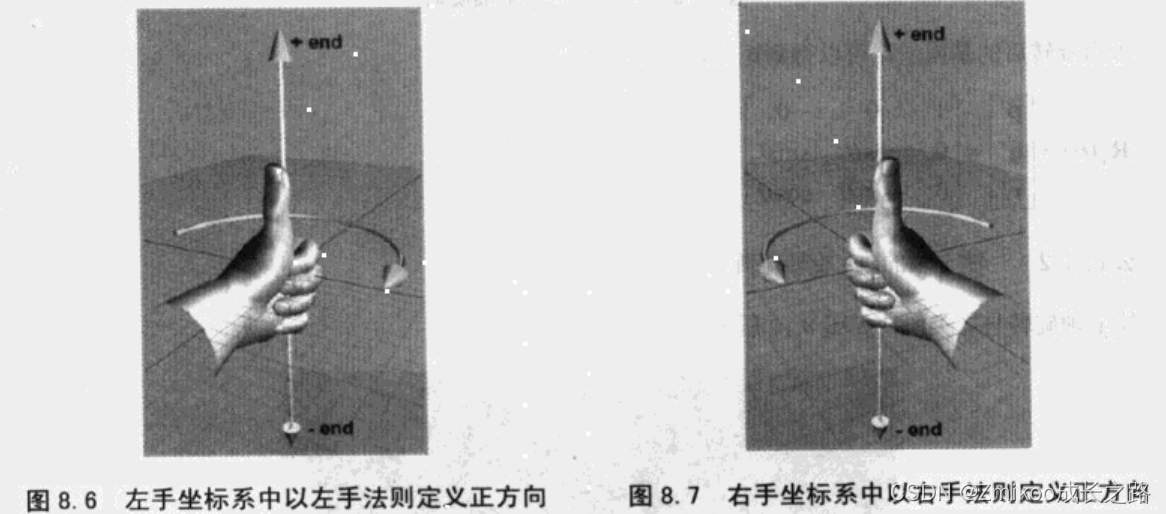
绕x轴旋转

旋转后的基向量
$R_x(\theta )=\left[\begin{array}{c}\vec{p}\prime \\ \vec{q}\prime \\ \vec{r}\prime \end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\theta & sin\theta \\ 0& -sin\theta & cos\theta \end{array}\right]$

绕Y轴与之类似：

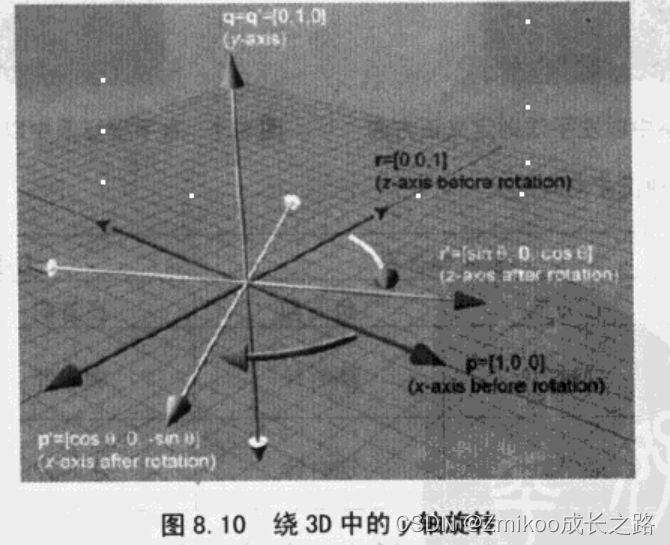
旋转后的基向量：
$R_y(\theta )=\left[\begin{array}{c}\vec{p}\prime \\ \vec{q}\prime \\ \vec{r}\prime \end{array}\right]=\left[\begin{array}{ccc}cos\theta & 0& -sin\theta \\ 0& 1& 0\\ sin\theta & 0& cos\theta \end{array}\right]$

绕z轴：

旋转后的基向量：
$R_z(\theta )=\left[\begin{array}{c}\vec{p}\prime \\ \vec{q}\prime \\ \vec{r}\prime \end{array}\right]=\left[\begin{array}{ccc}cos\theta & sin\theta & 0\\ -sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]$

绕任意轴旋转

由于不考虑平移，假设旋转轴通过原点。用单位向量 $\vec{n}$描述旋转轴，和前面一样用 $\theta$ 描述旋转量。也就是说，我们想得到满足下面条件的矩阵 $R(\vec{n},\theta )$:
$\vec{v}R(\vec{n},\theta )=\vec{v}\prime$ ($\vec{v}\prime$是 $\vec{v}$ 绕轴 $\vec{n}$ 旋转$\theta$后的向量)

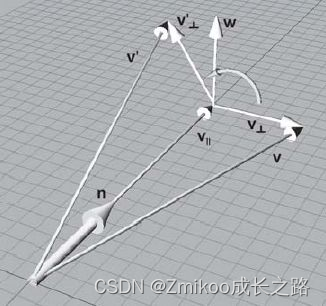
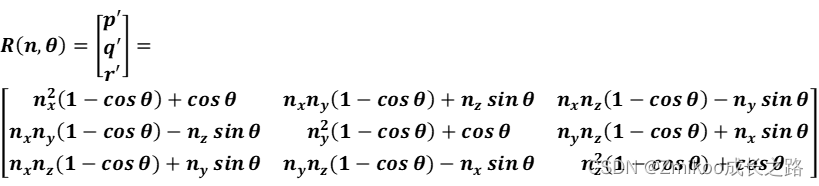
缩放

如果在各方向应用同比例的缩放(缩放因子$k$)，并且沿原点“膨胀”物体，那么就是均匀缩放。均匀缩放可以保持物体的角度和比例不变。如果长度增加或减小因子$k$ ，则面积增加或减小因子$k^2$，在3D中，体积的因子是$k^3$。
如果需要“挤压”或“拉伸”物体，在不同的方向应用不同的因子，这称作非均匀缩放。非均匀缩放时，物体角度将发生变化。视各方向缩放因子的不同，长度、面积、体积的变化因子也各不相同。
如果$\mid k\mid <1$，物体将“变短”;如果$\mid k\mid >1$，物体“变长”。如果 $k=0$，就是正交投影，如果$k<0$就是镜像。

沿坐标轴的缩放

2D中有两个缩放因子，$k_x$ 和 $k_y$。
基向量 $\vec{p}$ $\vec{q}$由相应的缩放因子单独影响：
$\vec{p}\prime =k_x\vec{p}=k_x[1,0]=[k_x,0]$
$\vec{q}\prime =k_y\vec{q}=k_y[0,1]=[0,k_y]$

用基向量构造矩阵：
$S(k_x,k_y)=\left[\begin{array}{c}\vec{p}\prime \\ \vec{q}\prime \end{array}\right]=\left[\begin{array}{cc}{k}_x& 0\\ 0& k_y\end{array}\right]$
3D需要增加第三个缩放因子$k_z$,3D的缩放矩阵：
$S(k_x,k_y,k_z)=\left[\begin{array}{ccc}{k}_x& 0& 0\\ 0& k_y& 0\\ 0& 0& k_z\end{array}\right]$

沿任意方向缩放

我们可以不依赖于坐标系而沿任意方向进行缩放。设 $\vec{n}$ 为平行于缩放方向的单位向量,$k$为缩放因子，缩放沿穿过原点并平行于 $\vec{n}$ 的直线(2D中)或平面(3D中)进行。

正交投影

一般来说，投影意味着降维操作。有一种投影方法是在某个方向上用零作为缩放因子。这种情况下，所有点都被拉平至垂直的轴(2D)或平面(3D)上。这种类型的投影称作正交投影，或者平行投影,因为从原来的点到投影点的直线相互平行。

向坐标轴或平面投影在实际变换中不常发生，大多数情况是向低维的变量赋值，且要抛弃维数时。例如，将3D点赋值给2D点，抛弃z分量，只复制x和y。
通过使垂直方向上的缩放因子为零，就能向坐标轴或平面投影。
向 $x$ 轴投影的2D矩阵：
$P_x=S([0,1],0)=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]$

向 $y$ 轴投影的2D矩阵：
$P_y=S([1,0],0)=\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]$

向 $xy$ 平面投影的3D矩阵：
$P_{xy}=S([0,0,1],0)=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]$

向 $xz$ 平面投影的3D矩阵：
$P_{xz}=S([0,1,0],0)=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right]$

向 $yz$ 平面投影的3D矩阵：
$P_{yz}=S([1,0,0],0)=\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$

向任意直线或平面投影

也能向任意直线或平面投影。由于不考虑平移，这些直线或平面必须通过原点。投影由垂直于直线或平面的单位向量$\vec{n}$定义。
通过使该方向的缩放因子为零能够导出向任意方向投影的矩阵。

镜像

镜像(也叫作反射)是一种变换，其作用是将物体沿直线(2D中)或平面(3D中)“翻折”。

使缩放因子为-1能够很容易地实现镜像变换。设$\vec{n}$为2D单位向量，下列矩阵将沿通过原点且垂直于$\vec{n}$的反射轴来进行镜像变换。

3D中，用反射平面代替直线。下列矩阵将沿通过原点且垂直于n的平面来进行镜像变换:

注意一个物体只能“镜像”一次，如果再次镜像(当沿不同的轴或平面的时候),物体将翻回“正面”(用一张纸来想象)，这和在原位置旋转物体的效果一样。

切变

切变是一种坐标系“扭曲”变换，非均匀地拉伸它。切变的时候角度会发生变化，但是面积和体积却保持不变。基本思想是将某一坐标的乘积加到另一个上。例如，2D中，将y乘以某个因子然后加到x上，得到$X^{\prime }=x+sy$。如图8.17所示。

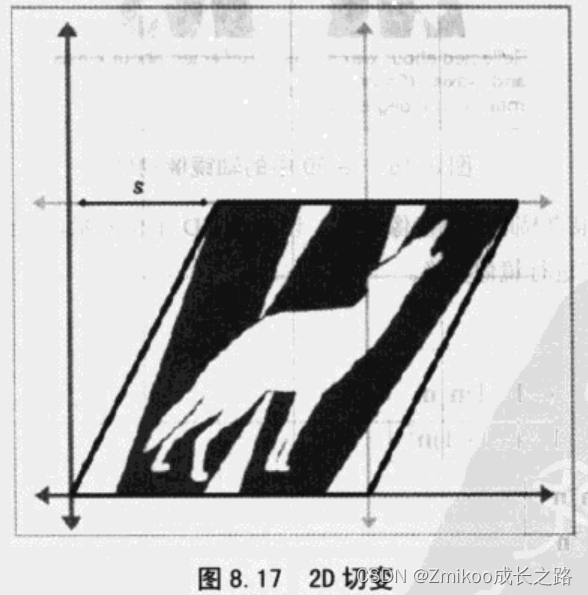
3D中的切变方法是取出一个坐标，乘以不同因子再加到其他两个坐标上。记法$H_{x}y$的意义是$x，y$坐标被坐标$z$改变。
切变是一种很少用到的变换，它也被称作扭曲变换。包含切变与缩放(均匀或非均匀)的变换通常很容易与包含旋转与非均匀缩放(只能是非均匀)的变换发生混淆。

变换的组合

变换分类

当讨论一般意义上的变换时，我们将使用类似的术语:映射或函数。在最一般的意义上，映射就是一种简单的规则，接收输入，产生输出。我们把从a到b的F映射记作$F(a)=b$。

线性变换

如果满足下式，那么映射$F(a)$就是线性的：
$F(a+b)=F(a)+F(b)$
$F(ka)=kF(a)$
线性变换的重要引理：

• 映射$F(a)=aM$,当$M$为任意方阵时，说映射是一个线性变换。
• $F(a+b)=(a+b)M=aM+bM=F(a)+F(b)$
• $F(ka)=(ka)M=k(aM)=kF(a)$

在某些文献中，线性变换的定义是平行线变换后仍然是平行线。大多数情况下它是对的，但有一个小小的例外:投影(当一条直线投影后变成一个点，能认为这个点平行于什么﹖)除了这点理论上的例外，这种定义是正确的。线性变换可能造成“拉伸”，但直线不会“弯折”，所以平行线仍然保持平行。

仿射变换

仿射变换是指线性变换后接着平移。因此，任何线性变换都是仿射变换，但不是所有仿射变换都是线性变换。
任何具有形式 $v^{\prime }=vM+b$ 的变换都是仿射变换。

可逆变换

如果存在一个逆变换可以“撤消”原变换，那么该变换是可逆的。即：如果存在逆变换$F^{-1}$，使得$F^{-1}(F(a))=a$，对于任意a，映射$F(a)$是可逆的。
一个仿射变换就是一个线性变换加上平移，显然，可以用相反的量“撤消”平移部分。所以问题变为一个线性变换是否可逆。
因为任意线性变换都能表达为矩阵，所以求逆变换等价于求矩阵的逆，如果矩阵是奇异的，则变换不可逆;可逆矩阵的行列式不为零。
除了投影以外，其他变换都能“撤消”。当物体被投影时，某一维有用的信息被抛弃了，而这些信息是不可能恢复的。因此，所有基本变换除了投影都是可逆的。

等角变换

如果变换前后两向量夹角的大小和方向都不改变，该变换是等角的。只有平移，旋转和均匀缩放是等角变换。等角变换将会保持比例不变。需要注意的是：镜像并不是等角变换，因为尽管两向量夹角的大小不变，但夹角的方向改变了。所有等角变换都是仿射和可逆的。

正交变换

“正交”用来描述具有某种性质的矩阵，正交变换的基本思想是轴保持互相垂直，而且不进行缩放变换。正交变换很容易求出它的逆。
平移、旋转和镜像是仅有的正交变换。长度、角度、面积和体积都保持不变。(尽管如此，但因为镜像变换被认为是正交变换，所以一定要密切注意角度、面积和体积的准确定义)。
正交矩阵的行列式为±1。
所有正交矩阵都是仿射和可逆的。

刚体变换

刚体变换只改变物体的位置和方向，不包括形状。所有长度、角度、面积和体积都不变。平移和旋转是仅有的刚体变换，镜像并不被认为是刚体变换。
刚体变换也被称作正规变换。所有刚体变换都是正交、等角、可逆和仿射的。
某些刚体变换旋转矩阵的行列式为1。

变换类型小结