机器学习笔记之深度信念网络(二)模型构建思想(RBM叠加结构)

引言

上一节介绍了深度信念网络的模型表示，本节将介绍深度信念网络的模型构建思想——受限玻尔兹曼机叠加结构的基本逻辑。

回顾：深度信念网络的结构表示

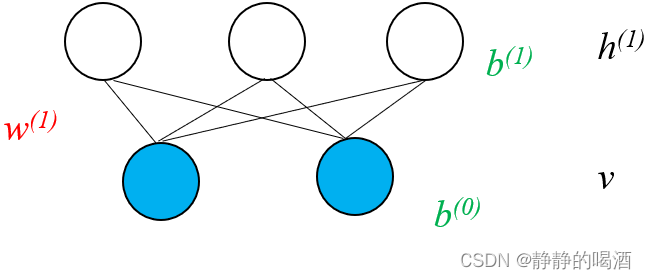
深度信念网络是一个基于有向图、无向图的混合模型。它的概率图结构表示如下：

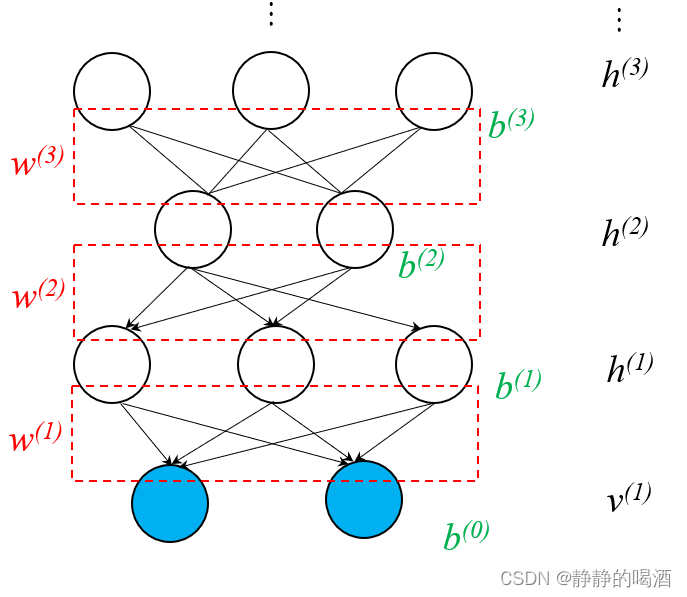
通过概率图结构的描述，可以发现：

• 观测变量层$v^{(1)}$，隐变量层$h^{(1)},h^{(2)}$三层的随机变量构成的概率图结构是Sigmoid信念网络；而隐变量层$h^{(2)},h^{(3)}$构成的概率图结构是受限玻尔兹曼机。
• 通过对受限玻尔兹曼机的堆叠(Stacking)实现对深度信念网络向更深层次进行延伸。
  这里使用省略号替代了后续的堆叠部分。

如果将随机变量层$v^{(1)},h^{(1)},h^{(2)},h^{(3)},\cdots$看作是关于对应层所有随机变量的集合，那么联合概率分布则表示为：
这里仍然以$v^{(1)},h^{(1)},h^{(2)},h^{(3)}$这四层结构进行示例。
$$\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})$$
实际上，非相邻层之间存在条件独立性。

• 例如：$v^{(1)}$层与$h^{(2)}$层。这明显是有向图结构中的顺序结构。在$h^{(1)}$层可观测的条件下，$h^{(2)}$层中的任意结点与$v^{(1)}$层之间条件独立：
  $$h^{(2)}\perp v^{(1)}\mid h^{(1)}$$
• 上述只是有向图结构。如果是混合结构呢？例如：$h^{(1)}$层与$h^{(3)}$层。虽然既包含有向图结构，也包含无向图结构，但它们依然满足条件独立性：
  $$h^{(1)}\perp h^{(3)}\mid h^{(2)}$$
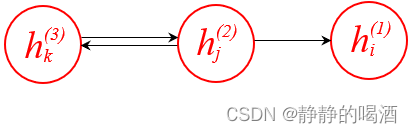
  以$h^{(1)},h^{(2)},h^{(3)}$层中的某一组结构为例，具体概率图结构表示如下(红色路径)：
  
  从有向图的角度观察，可以将红色部分表示为如下形式。如果在隐变量$h_j^{(2)}$给定的条件下，隐变量$h_k^{(3)},h_i^{(1)}$之间要么是顺序结构关系，要么是同父结构关系，依然改变不了条件独立的本质。
  

至此，联合概率分布$\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})$可表示为：
$$\begin{array}{rl}\mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})& =\mathcal{P}(v^{(1)}\mid h^{(1)},h^{(2)},h^{(3)})\cdot \mathcal{P}(h^{(1)},h^{(2)},h^{(3)})\\ & =\mathcal{P}(v^{(1)}\mid h^{(1)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)},h^{(3)})\cdot \mathcal{P}(h^{(2)},h^{(3)})\\ & =\mathcal{P}(v^{(1)}\mid h^{(1)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)})\cdot \mathcal{P}(h^{(2)},h^{(3)})\end{array}$$
根据Sigmoid信念网络与受限玻尔兹曼机的定义，展开结果表示如下：
$$\begin{array}{rl}& \mathcal{P}(v^{(1)},h^{(1)},h^{(2)},h^{(3)})=\prod _{i=1}^{\mathcal{D}}\mathcal{P}(v_i^{(1)}\mid h^{(1)})\cdot \prod _{j=1}^{{\mathcal{P}}^{(1)}}\mathcal{P}(h_j^{(1)}\mid h^{(2)})\cdot \mathcal{P}(h^{(2)},h^{(3)})\\ & \{\begin{array}{l}\mathcal{P}(v_i^{(1)}\mid h^{(1)})=\text{Sigmoid}\left\{{\left[{\mathcal{W}}_{h^{(1)}\to v_i^{(1)}}\right]}^T{h}^{(1)}+b_i^{(0)}\right\}{\left[{\mathcal{W}}_{h^{(1)}\to v_i^{(1)}}\right]}_{{\mathcal{P}}^{(1)}\times 1}\in {\mathcal{W}}^{(1)}\\ \mathcal{P}(h_j^{(1)}\mid h^{(2)})=\text{Sigmoid}\left\{{\left[{\mathcal{W}}_{h^{(2)}\to h_j^{(1)}}\right]}^T{h}^{(2)}+b_j^{(1)}\right\}{\left[{\mathcal{W}}_{h^{(2)}\to h_j^{(1)}}\right]}_{{\mathcal{P}}^{(2)}\times 1}\in {\mathcal{W}}^{(2)}\\ \mathcal{P}(h^{(2)},h^{(3)})=\frac{1}{\mathcal{Z}}\exp \left\{{\left[h^{(3)}\right]}^T{\mathcal{W}}^{(3)}\cdot h^{(2)}+{\left[h^{(2)}\right]}^T\cdot b^{(2)}+{\left[h^{(3)}\right]}^T{b}^{(3)}\right\}\end{array}\end{array}$$

解析RBM隐变量的先验概率

深度信念网络被设计成$\text{Sigmoid}$信念网络与若干受限玻尔兹曼机的叠加结构，它的设计思路具体是什么？
回顾受限玻尔兹曼机。其概率图结构表示如下：

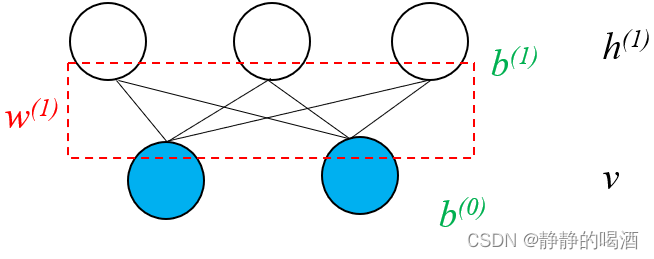
其中${\mathcal{W}}^{(1)}$表示隐变量、观测变量之间关联关系的权重信息；$b^{(0)},b^{(1)}$分别表示观测变量、隐变量的偏置信息。在受限玻尔兹曼机——对数似然梯度求解中，介绍了关于 模型参数$\theta$ 的求解过程：

• 根据已知样本 V = { v ( i ) } i = 1 N \mathcal V = \{v^{(i)}\}_{i=1}^N V={v(i)}i=1N​使用极大似然估计方法进行求解。其目标函数$\mathcal{L}(\theta )$表示为：
  $$\mathcal{L}(\theta )=\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}\log \mathcal{P}(v^{(i)};\theta )$$
  对应模型参数的对数似然梯度可表示为：
  $${\nabla }_{\theta }\mathcal{L}(\theta )=\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}{\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]$$
• 根据能量模型的对数似然梯度，将${\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]$表示为如下形式：
  $${\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]=\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}-\sum _{v^{(i)}}\mathcal{P}(v^{(i)})\cdot \mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}\theta ={\mathcal{W}}_{h_k^{(i)}\iff v_j^{(i)}}$$
  关于第一项：可以通过$\text{Sigmoid}$函数直接求解后验概率$\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})$；
  关于第二项：它是关于$N$项的连加，其计算量极高。因而通过使用对比散度的方式对第二项进行近似：
  这里的$t$表示吉布斯采样的迭代步骤。
  $$\sum _{v^{(i)}}\mathcal{P}(v^{(i)})\cdot \mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}={\mathbb{E}}_{v^{(k)}\sim \mathcal{P}({\mathcal{V}}^{t=k})}\left[\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}\right]$$
• 关于参数${\mathcal{W}}_{h_k^{(i)}\iff v_j^{(i)}}$的梯度求解完成后，使用梯度上升法近似求解${\mathcal{W}}_{h_k^{(i)}\iff v_j^{(i)}}$。其余参数同理：
  $${\theta }^{(t+1)}\Leftarrow {\theta }^{(t)}+\eta {\nabla }_{\theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]\theta ={\mathcal{W}}_{h_k^{(i)}\iff v_j^{(i)}}$$

观察，上述关于模型参数的学习过程是复杂的，并且包含两次近似(对比散度、梯度上升)，其核心原因在于：受限玻尔兹曼机是一个无向图模型，随机变量结点之间没有明确的因果关系。
能否通过一些改进，让参数学习过程的效果更好？
以上述受限玻尔兹曼机概率图结构示例，再次将关注点转向$\mathcal{P}(v)$：
这里的上标就变成了网络层的编号，而不是样本编号。
$$\begin{array}{rl}\mathcal{P}(v)& =\sum _{h^{(1)}}\mathcal{P}(h^{(1)},v)\\ & =\sum _{h^{(1)}}\mathcal{P}(h^{(1)})\cdot \mathcal{P}(v\mid h^{(1)})\end{array}$$

• 其中$h^{(1)}$可看成$\text{RBM}$中所有隐变量的随机变量集合，$v$则是所有观测变量的随机变量集合，而$h^{(1)}$中的随机变量不是真实的，而是基于模型假定的。因此，称$\mathcal{P}(h^{(1)})$为 先验概率；
• 而$\mathcal{P}(v\mid h^{(1)})$则是给定隐变量条件下，样本的 生成过程(Generative Process)。
  这些样本自然不是真实的，而是模型产生的‘幻想粒子’(Fantasy Particle).与幻想粒子相关的传送门

由于是无向图模型，因而同上，从有向图的角度观察，可以将图结构中的每一条边视作双向的。也就是相互关联：

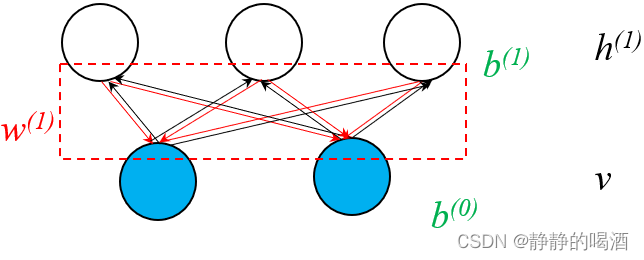
如果假设模型参数已经被学习完成，这意味着模型参数固定，$\mathcal{P}(v\mid h^{(1)})$也被固定住：
这里的$n$表示模型中观测变量的数量,$m$表示模型中隐变量的数量。相关推导过程见RBM推断任务——后验概率
$$\begin{array}{rl}\mathcal{P}(v\mid h^{(1)})& =\prod _{i=1}^n\mathcal{P}(v_i\mid h^{(1)})\\ \mathcal{P}(v_i\mid h)& =\{\begin{array}{l}\mathcal{P}(v_i=1\mid h)\Rightarrow \text{Sigmoid}\left({\sum }_{j=1}^m{w}_{ij}\cdot h_j+b_i\right)\\ \mathcal{P}(v_i=0\mid h)\Rightarrow 1-\text{Sigmoid}\left({\sum }_{j=1}^m{w}_{ij}\cdot h_j+b_i\right)\end{array}\end{array}$$
而$\mathcal{P}(v)$是真实样本关于随机变量的联合概率分布，自然是确定的：
相关推导过程详见RBM推断任务——边缘概率,这里的$b$表示各观测变量与自身的关联关系(常数，偏置)组成的向量。
$$\mathcal{P}(v)=\frac{1}{\mathcal{Z}}\exp \left\{b^{T}v+\sum _{j=1}^m\log \text{Softplus}({\mathcal{W}}_j^{T}v+c_j)\right\}$$
那么根据上式，先验概率$\mathcal{P}(h^{(1)})$自然也是确定的，它同样可以使用模型参数进行表示。

通过模型学习隐变量的先验概率

相比于使用模型参数表示先验概率$\mathcal{P}(h^{(1)})$，一个新的思路是：针对隐变量先验概率$\mathcal{P}(h^{(1)})$进行建模，通过模型将$\mathcal{P}(h^{(1)})$学习出来。也就是说，通过的受限玻尔兹曼机将隐变量的联合概率分布求解出来。

观察上图(黑色箭头)，利用真实样本使用醒眠算法的$\text{Weak Phase}$方法能够获得关于隐变量后验的样本，并基于这些样本，专门对隐变量进行训练：
也就是说，为了学习‘Sigmoid信念网络’中的隐变量，需要对隐变量进行建模，构建‘隐变量的隐变量’对其进行学习。

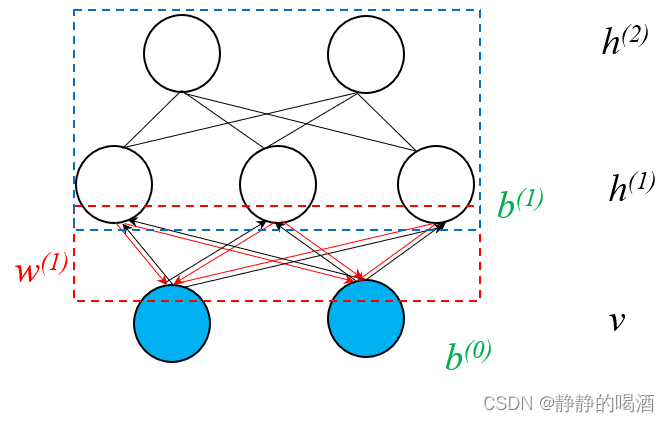
此时，关于$h^{(1)}$的边缘概率分布可表示为：
$$\sum _{h^{(2)}}\mathcal{P}(h^{(1)},h^{(2)})$$
很明显，$\mathcal{P}(h^{(1)},h^{(2)})$就是新构建受限玻尔兹曼机(蓝色框部分)的联合概率分布。此时将$h^{(1)}$在受限玻尔兹曼机中视作观测变量，基于$\mathcal{P}(h^{(1)}\mid v)$的后验样本，可以学习出该受限玻尔兹曼机的参数信息。通过这些参数信息产生的关于$h^{(1)}$的概率分布$\mathcal{P}(h^{(1)})$要优于原始模型参数学习的$\mathcal{P}(h^{(1)})$。

事实上，根据第一层受限玻尔兹曼机的逻辑，我们理论上可以将层数一直叠加上去，通过构建新的隐变量学习前一层隐变量的信息。
需要注意的是，这种堆叠式结构的求解方式是有约束条件的。那就是Weak Phase中关于隐变量$h^{(1)}$的后验概率分布$\mathcal{P}(h^{(1)}\mid v)$固定的条件下实现的。

• 如果不去固定$\mathcal{P}(h^{(1)}\mid v)$,在$h^{(2)}$学习$\mathcal{P}(h^{(1)})$过程中，由于$\mathcal{P}(h^{(1)}\mid v)$产生样本对应分布的细微变化(可能存在波动、噪声)，导致$h^{(1)},h^{(2)}$层之间的模型参数是无法被固定下来的。
• 相反，如果没有固定$\mathcal{P}(h^{(1)}\mid v)$,假设$h^{(1)},h^{(2)}$之间的模型参数被学习出来，学习得到的$\mathcal{P}(h^{(1)})$和$\mathcal{P}(h^{(1)}\mid v)$之间存在偏差，反而对$h^{(1)},v$层之间的权重信息产生影响。
当然，也可以从有向图的角度去理解该问题。如果出现了如下结构：
  
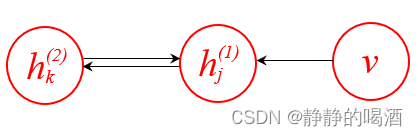
  这种结构保留了$v\Rightarrow h^{(1)}$之间的关联关系，我们会发现，$v,h^{(2)}$之间不是完全的‘无关联’关系。因为内部包含一个$\mathcal{V}$型结构。一旦经过$\text{Weak Phase}$算法，得到了关于后验$\mathcal{P}(h^{(1)}\mid v)$的样本，此时结点$h^{(1)}$被观测，那么$h^{(2)},v$之间是必不独立的。

终上，为了保证学习$h^{(1)}$信息的受限玻尔兹曼机和$\text{Sigmoid}$信念网络之间相互不影响，将上图中 $v\Rightarrow h^{(1)}$ 部分去除：

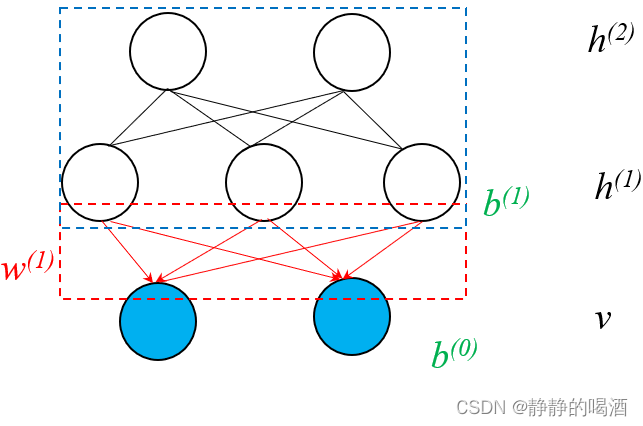
上面过程就是深度信念网络模型的构建思想。

小插曲：杰森不等式(2023/1/11)

关于杰森不等式，它主要描述凸函数值与凸函数积分之间之间大小关系的不等式。其具体描述为：已知函数$f(x)$是一个凸函数(Convex Function)，则有下式恒成立：
$$\mathbb{E}[f(x)]\ge f(\mathbb{E}[x])$$

杰森不等式的数学证明

证明过程：

• 已知凸函数表示为如下形式：
  
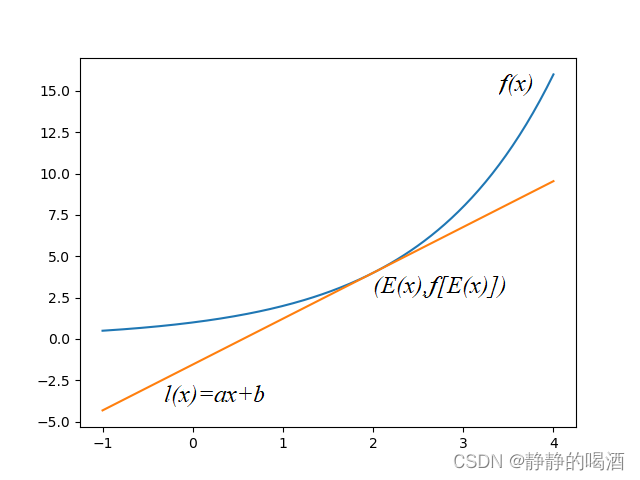
  其中$\mathbb{E}[x]$表示$x$的期望结果，并且由于$x$是一维常量，那么其期望$\mathbb{E}[x]$同样是一个常数，并落在$x$轴上。因而关于点$(\mathbb{E}[x],f(\mathbb{E}[x]))$作一条与凸函数$f(x)$的切线，并记作该直线的方程为：$l(x)=ax+b$。
  此时，点$(\mathbb{E}[x],f(\mathbb{E}[x]))$同时满足两个函数：
  $$f(\mathbb{E}[x])=l(\mathbb{E}[x])=a\mathbb{E}[x]+b$$
• 由于$f(x)$是凸函数，根据凸函数的性质：对于$\forall x$,均有：
  $f(x)$的图像均在$l(x)$上方。
  $$f(x)\ge l(x)$$
• 将不等式两边同时求解期望，不等号不发生变化：
  根据期望的运算性质，将$\mathbb{E}[ax+b]$展开。$b$是常数，期望$\mathbb{E}[b]$是其本身。
  $$\begin{array}{rl}\mathbb{E}[f(x)]& \ge \mathbb{E}[l(x)]\\ & =\mathbb{E}[ax+b]\\ & =a\mathbb{E}[x]+b\\ & =f[\mathbb{E}[x]]\end{array}$$

叠加RBM的优势

为什么 对隐变量建模 比模型参数学习隐变量的效果更优？

• 首先回顾受限玻尔兹曼机关于观测变量(样本数据)的对数似然函数：
  引入隐变量$h^{(1)}$.
  
  $$\begin{array}{r}\log \mathcal{P}(v)=\log \sum _{h^{(1)}}\mathcal{P}(v,h^{(1)})\end{array}$$
• 基于变分推断的思想，引入一个关于隐变量的后验概率分布$\mathcal{Q}(h^{(1)}\mid v)$，具体表示结果如下：
  将积分部分视作关于概率分布$\mathcal{Q}(h^{(1)}\mid v)$的期望形式。
  $$\begin{array}{rl}\log \mathcal{P}(v)& =\log \sum _{h^{(1)}}\mathcal{Q}(h^{(1)}\mid v)\cdot \frac{\mathcal{P}(v,h^{(1)})}{\mathcal{Q}(h^{(1)}\mid v)}\\ & =\log \left\{{\mathbb{E}}_{\mathcal{Q}(h^{(1)}\mid v)}\left[\frac{\mathcal{P}(v,h^{(1)})}{\mathcal{Q}(h^{(1)}\mid v)}\right]\right\}\end{array}$$
  由于$\log$函数是一个典型的凹函数，根据杰森不等式，下面等式恒成立：
  $$\log \left\{{\mathbb{E}}_{\mathcal{Q}(h^{(1)}\mid v)}\left[\frac{\mathcal{P}(v,h^{(1)})}{\mathcal{Q}(h^{(1)}\mid v)}\right]\right\}\ge {\mathbb{E}}_{\mathcal{Q}(h^{(1)}\mid v)}\left\{\log \left[\frac{\mathcal{P}(v,h^{(1)})}{\mathcal{Q}(h^{(1)}\mid v)}\right]\right\}$$
  将不等式右侧展开，可写成：
  $$\begin{array}{rl}{\mathbb{E}}_{\mathcal{Q}(h^{(1)}\mid v)}\left\{\log \left[\frac{\mathcal{P}(v,h^{(1)})}{\mathcal{Q}(h^{(1)}\mid v)}\right]\right\}& =\sum _{h^{(1)}}\mathcal{Q}(h^{(1)}\mid v)\log \frac{\mathcal{P}(v,h^{(1)})}{\mathcal{Q}(h^{(1)}\mid v)}\\ & =\sum _{h^{(1)}}\mathcal{Q}(h^{(1)}\mid v)\left[\log \mathcal{P}(v,h^{(1)})-\log \mathcal{Q}(h^{(1)}\mid v)\right]\end{array}$$
  很明显，该格式就是关于随机变量$h^{(1)},v$证据下界(Evidence of Lower Bound,ELBO)的表达格式。

比较受限玻尔兹曼机和深度信念网络之间，通过增加一层变量$\text{ELBO}$的变化情况：

• 基于受限玻尔兹曼机的逻辑，$\text{ELBO}$达到最大时，概率分布$\mathcal{Q}(h^{(1)}\mid v)$近似隐变量的后验分布$\mathcal{P}(h^{(1)}\mid v)$(被确定)。从而通过模型参数确定$\log \mathcal{P}(v,h^{(1)})$。
• 从深度信念网络的逻辑，可以将$\log \mathcal{P}(v,h^{(1)})$继续展开：
  这里为简化描述，将$\text{ELBO}$简写成$\Delta$.
  $$\begin{array}{rl}\Delta & =\sum _{h^{(1)}}\mathcal{Q}(h^{(1)}\mid v)\left[\log \mathcal{P}(v,h^{(1)})-\log \mathcal{Q}(h^{(1)}\mid v)\right]\\ & =\sum _{h^{(1)}}\mathcal{Q}(h^{(1)}\mid v)\left\{\log \left[\mathcal{P}(h^{(1)})\cdot \mathcal{P}(v\mid h^{(1)})\right]-\log \mathcal{Q}(h^{(1)}\mid v)\right\}\\ & =\sum _{h^{(1)}}\mathcal{Q}(h^{(1)}\mid v)\left\{\log \mathcal{P}(h^{(1)})+\log \mathcal{P}(v\mid h^{(1)})-\log \mathcal{Q}(h^{(1)}\mid v)\right\}\\ & =\sum _{h^{(1)}}\mathcal{Q}(h^{(1)}\mid v)\log \mathcal{P}(h^{(1)})+\underset{=\mathcal{C}}{\underbrace{\sum _{h^{(1)}}\mathcal{Q}(h^{(1)}\mid v)\left[\log \frac{\mathcal{P}(v\mid h^{(1)})}{\mathcal{Q}(h^{(1)}\mid v)}\right]}}\\ & =\sum _{h^{(1)}}\mathcal{Q}(h^{(1)}\mid v)\log \mathcal{P}(h^{(1)})+\mathcal{C}\end{array}$$
  由于此时关于后验$\mathcal{Q}(h^{(1)}\mid v)$的样本被观测到，因而幻想粒子的生成分布$\mathcal{P}(v\mid h^{(1)})$是确定的。从而将后项视作常数$\mathcal{C}$。
  而$h^{(1)}$层基于后验分布$\mathcal{Q}(h^{(1)}\mid v)$采样得到的样本，构建一个新的RBM进行学习，最终目标是：学习新的表示$h^{(1)}$的模型参数，使$\mathcal{P}(h^{(1)})$的对数似然函数达到最大。
  这是‘受限玻尔兹曼机’学习任务的意义。给定样本(观测变量信息)，并选定受限玻尔兹曼机作为模型，使得$\hat{\theta }=\underset{\theta }{\mathrm{argmax}}\log \mathcal{P}(v;\theta )$,从而得到模型参数$\theta$;
  只不过此时将$v$替换成了$h^{(1)}$,并且样本同样是基于上一步产生的$\text{Sample from }\mathcal{Q}(h^{(1)}\mid v)$，通过$\underset{\varphi }{\mathrm{argmax}}\log P(h^{(1)};\varphi )$自然可以得到一组描述$\mathcal{P}(h^{(1)})$的模型参数$\varphi$.

也就是说，构建新变量层的目的就是最大化$\log \mathcal{P}(h^{(1)})$，$\log \mathcal{P}(h^{(1)})$增大了，那么对应的$\text{ELBO}$同样会提升到极致。从而最终使$\log \mathcal{P}(v)$相比之前会有所提升。
如果从$\mathcal{P}(h^{(1)})$的角度观察：

• 受限玻尔兹曼机仅凭真实样本产生的$\mathcal{P}(h^{(1)},v)$和$\mathcal{P}(v\mid h^{(1)})$去计算$\mathcal{P}(h^{(1)})$;这个结果是基于真实样本产生的，它是真实的，但并不一定是最优的;
• 而深度信念网络产生的$\mathcal{P}(h^{(1)})$是基于算法理论上的最大值。学习叠加RBM使用的就是‘极大似然估计’。

相关参考：
(系列二十七)深度信念网络2——叠加RBM的动机
(系列二十七)深度信念网络3——叠加RBM可增加ELBO
机器学习-数学基础-概率-不等式1-杰森不等式