离散时间信号与系统
matlab里面冲击序列表示方法:
function[x,n]=impseq(n0,n1,n2)
%generate x(n)=delta(n-n0);n1<=n<=n2
%---------------------------------
%[x,n]=impseq(n0,n1,n2)
%
n=[n1:n2];x=[(n-n0)==0];matlab里面阶跃序列表示方法:
function[x,n]=stepseq(n0,n1,n2)
%generate x(n)=u(n-n0);n1<=n<=n2
%---------------------------------
%[x,n]=stepseq(n0,n1,n2)
%
n=[n1:n2];x=[(n-n0)>=0];实指数序列。并且以n为横坐标,x为纵坐标,作图
function[x]=expon(a)
% generate real exponential sequence x[n]=a^n
n=[0:1:10];
x=a.^n;
stem(n,x,'b');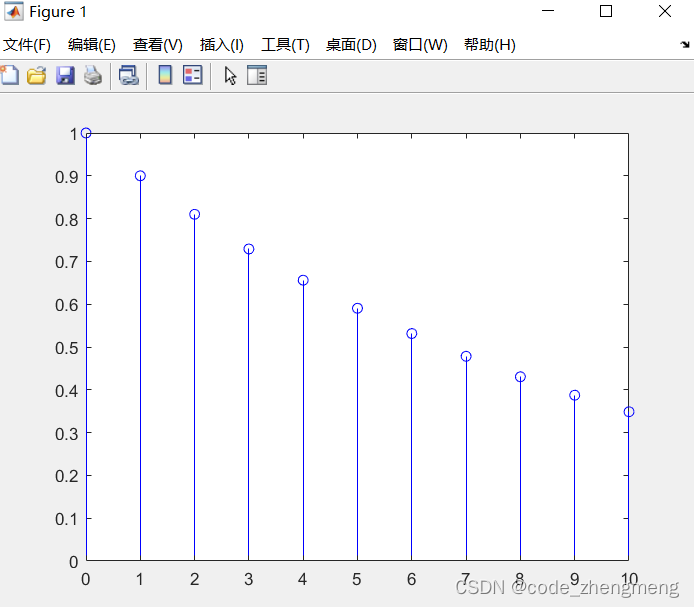
复指数序列:
function[x]=expone(a,b)
% generate real exponential sequence x[n]=exp()
n=[0:1:10];
x=exp((a+b*j)*n);正弦序列
n=[0:1:10];
x=3*cos(0.1*pi*n+pi/3)+2*sin(0.5*pi*n)随机序列
rand(1,N)产生一个长度为N,其值在[0,1]之间均匀分布的随机序列;randn(1,N)产生一个长度为N,均值为0,方差为1的高斯随机序列。
周期序列
function[x]=Periodic(n,p)
%generate Periodic sequence
%where n represents the initial sequence
%and p represents the number of repetitions
x=n'*ones(1,p);
x=x(:);%将x矩阵一列一列的取出,并排列,变成一个n*1的矩阵序列的相关性
目的:看两个序列的相似程度,相关值越大,越相关
实序列互相关:
实序列自相关:
举个例子,序列,与序列
,互相关,代码如下:
nx=0:6;x=[3 5 -7 2 -1 -3 2];
ny=2:8; y0=x;
w=randn(1,length(y0));
y=y0+w;
ryx=xcorr(y,x);
nryx=-4:8;
stem(nryx,ryx,'r','linewidth',2);
xlabel('nryx');ylabel('ryx');结果如下:
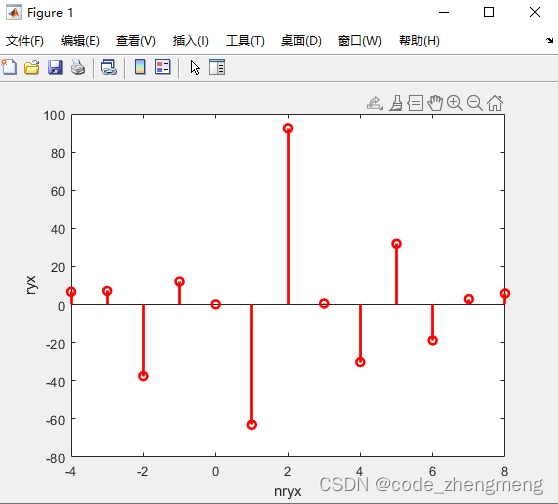
结论:在n=2的时候相关值最大
MATLAB实现差分传递推解的函数
b=0.5; %x的各项系数
a=[1,-0.5]; %y的各项系数,从低阶往高阶延时
x=ones(1,100);
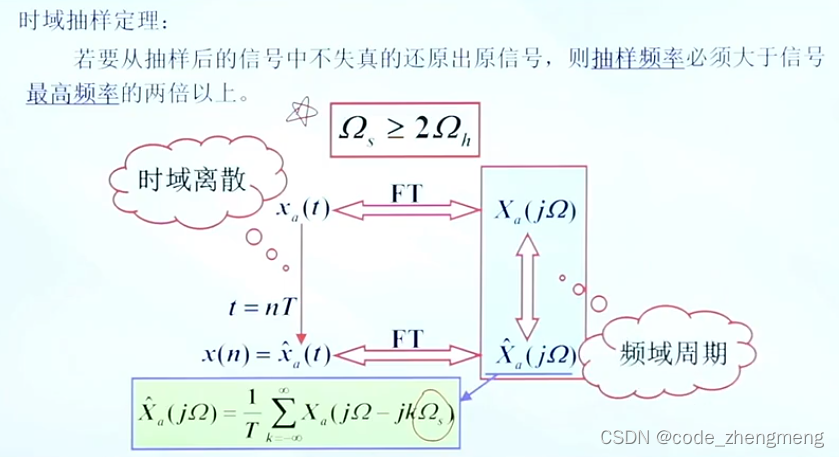
y=filter(b,a,x);采样定理
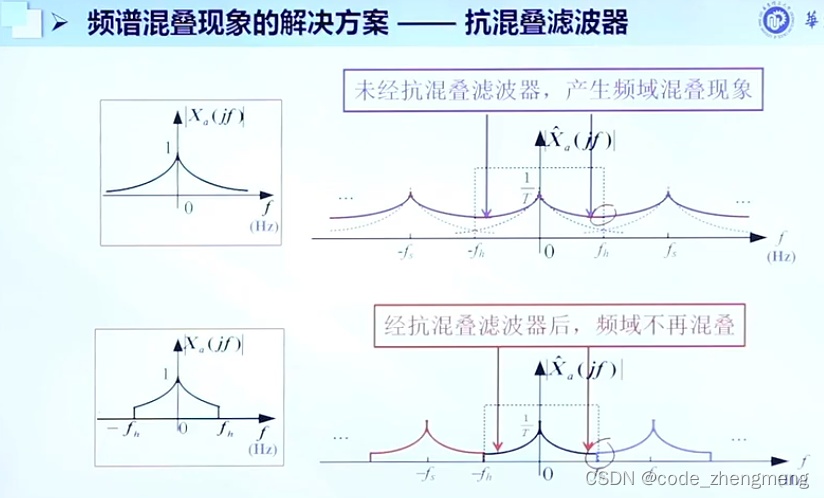
低通信号的采样要满足奈奎斯特采样定理,即:采样频率和低通信号的最高频
满足:
,便可以保证采样之后的频谱不发生交叠,当
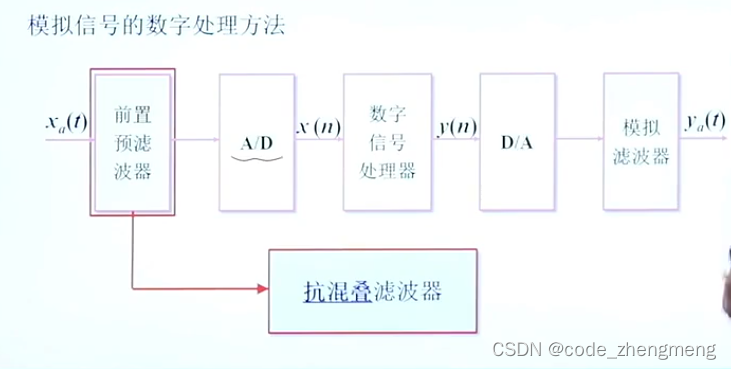
时,就是奈奎斯特采样定理。数字信号处理中,在采样之前,往往需要通过一个预处理器,其目的是将低通信号限制在一个频率范围之内,防止采样之后的频谱发生交叠。
对于带通信号,当,其中
整数,
是带宽,即带通信号的最高频率是带宽的整数倍时,则选择抽样频率
,采样后的频谱不会发生混叠现象,只要通过合适的带通滤波器便可以恢复原始信号。
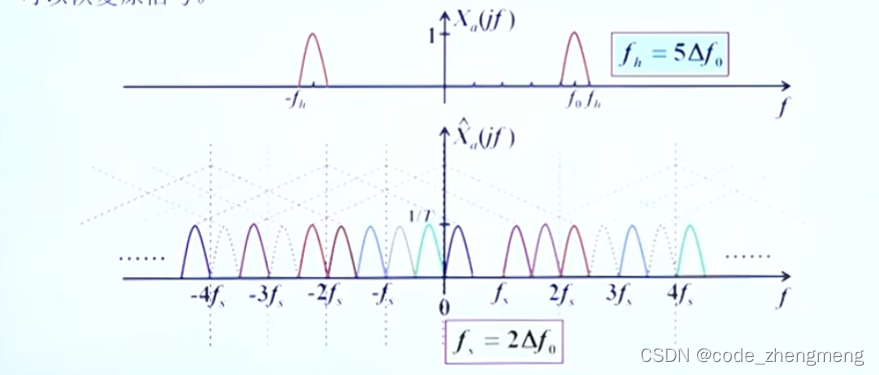
带通信号中,,其中
不是整数,则将通带下端延申到使其带宽为
,且满足:
,此时r为整数,然后用上述带通信号的方法抽样。
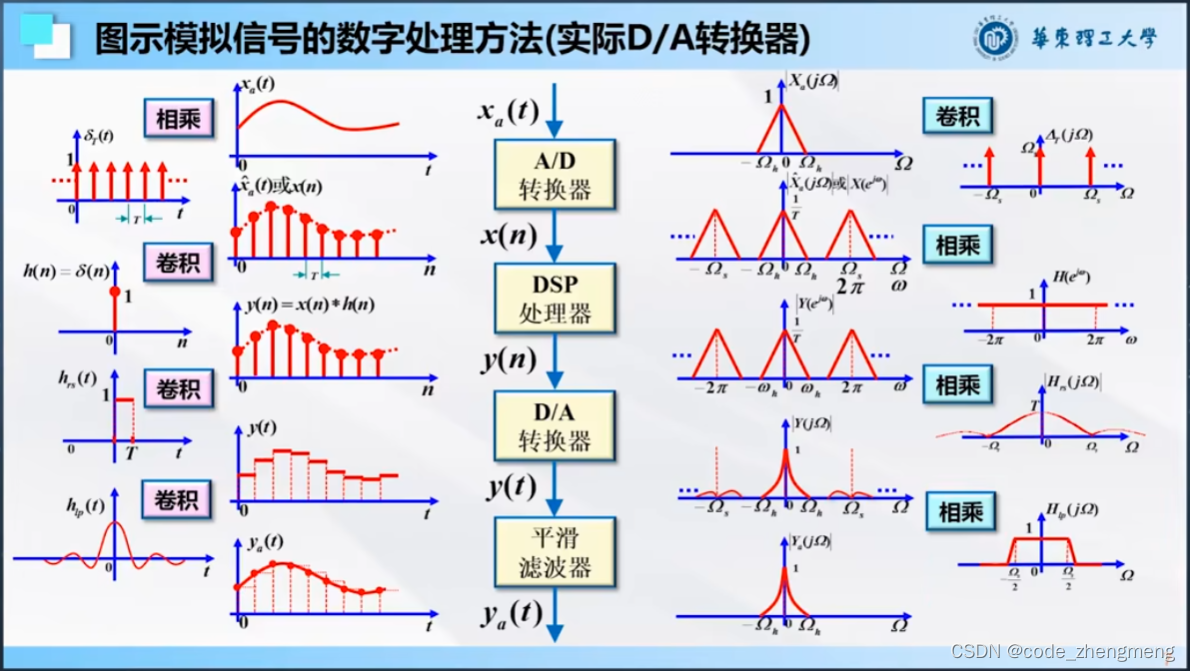
模拟信号的数字处理方法
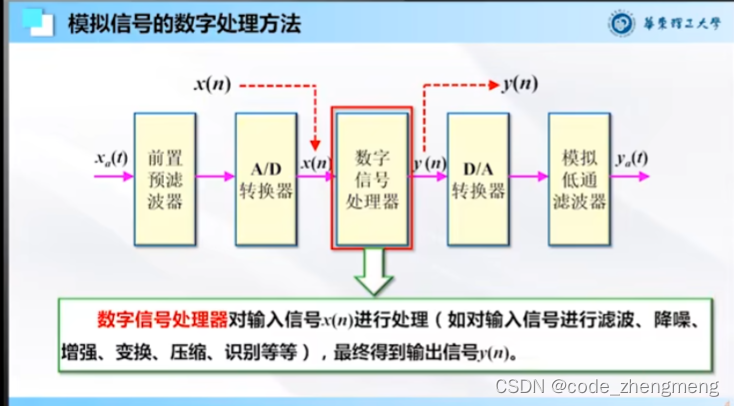
零阶保持器:理想采样信号在实际中是不可实现的,实际中采样的信号是矩形信号,在一段时间维持矩形信号电平不变的器件就是零阶保持器。
平滑滤波器:平滑滤波器在时域上就是把信号变得平滑,在频域上是滤除信号的高频的成分。
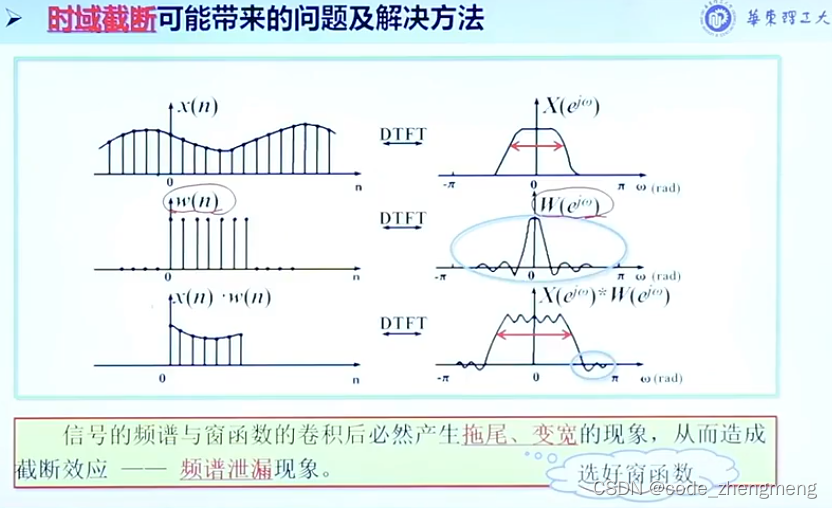
离散时间信号傅里叶变换的基本概念
正变换:
反变换:
说明:①正变换的收敛条件为:
若序列绝对可和,则他的傅里叶变换存在且连续。
②的特性:
由于时域上的离散,使得频域上的
出现周期的特性,周期为
 正变换和反变换的由来
正变换和反变换的由来
①正变换:可由变换定义得到
②反变换:若序列的变换在单位圆上收敛时:
共轭对称序列和共轭反对称序列
共轭对称序列:
实部是偶函数,虚部是奇函数
共轭反对称序列:
实部是奇函数,虚部是偶函数
由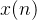 表示
表示 和
和
关于频域函数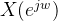 的共轭对称性质描述
的共轭对称性质描述
共轭对称序列:
共轭反对称序列:
时域与频域对应的共轭对称性质
①序列实部的傅里叶变换等于序列傅里叶变换的共轭对称分量
②序列虚部的傅里叶变换等于序列傅里叶变换的共轭反对称分量
③序列的共轭对称分量和共轭反对称分量的分别等于序列傅里叶变换的实部和虚部
④特殊情况:当为实序列,
应该只剩下共轭对称分量(实序列无虚部,所以无共轭反对称分量)
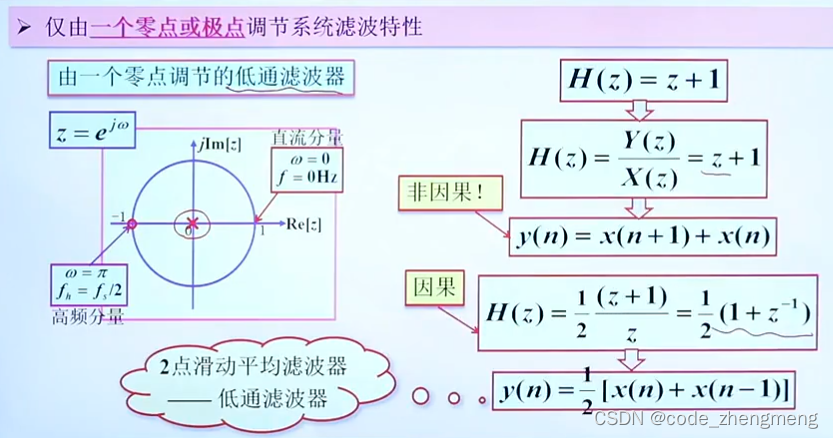
设计数字滤波器的一般原则
1.若使设计的滤波器拒绝某一个频率(不让该信号通过),应在单位圆上相应频率处设置一个零点
2.若使设计的滤波器突出某个频率(使该信号尽可能无衰减的通过),应在单位圆内相应的频率处设置一个极点,极点越接近单位圆,该频率处的幅频响应值越大
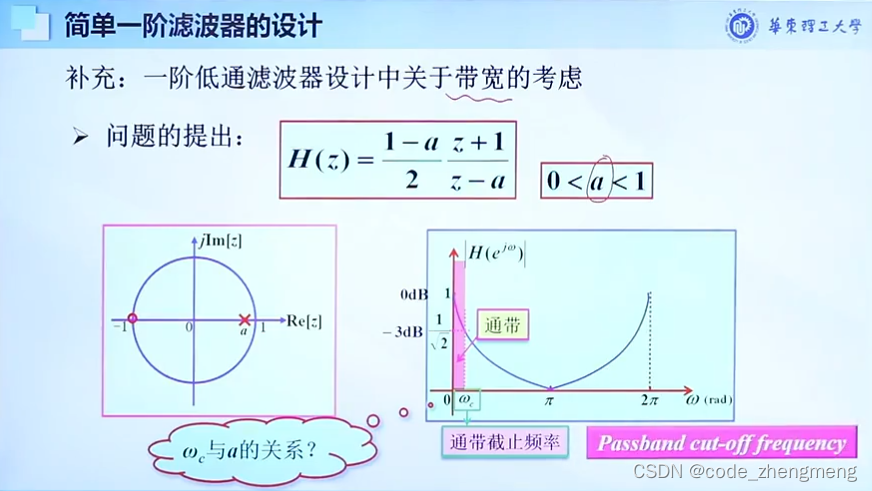
简单一阶滤波器设计
仅由一个零点或极点调节系统滤波特性
由一个零点调节的低通滤波器
注意:数字角频率与的对应比例关系如下:
对应
;
那么对应

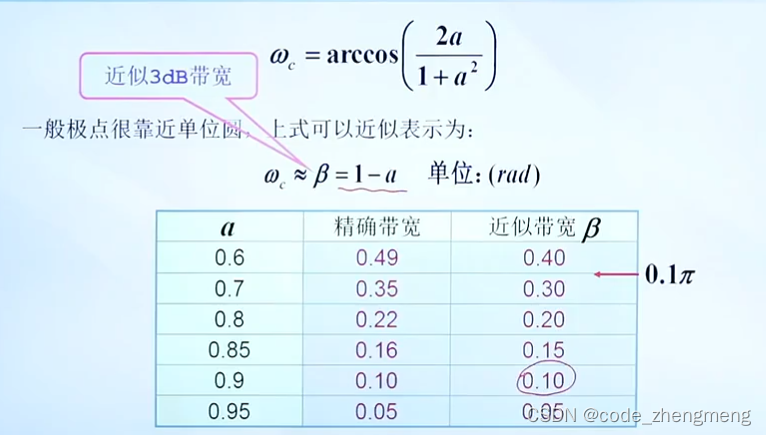


傅里叶级数、傅里叶变换、离散时间信号傅里叶变换

从傅里叶变换FT到序列傅里叶变换DFTFT

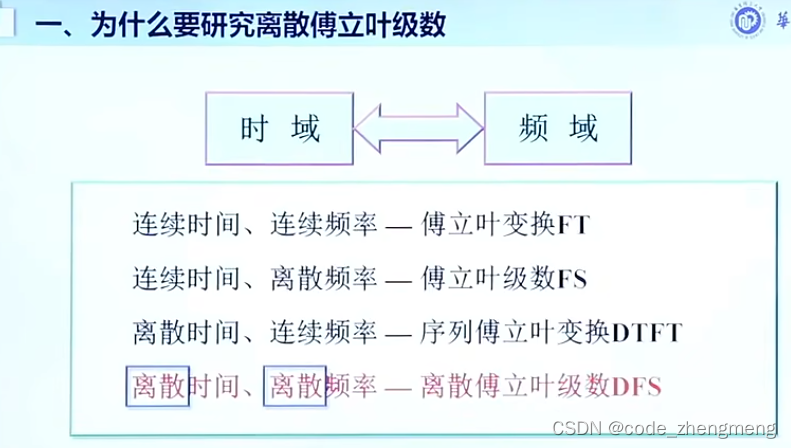
为什么要研究DFS?
因为我们希望时域和频域处理的信号都是离散的
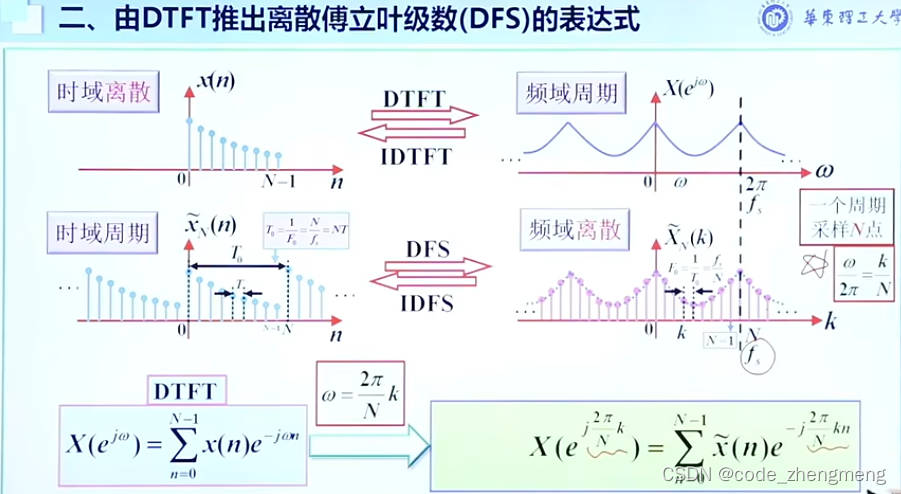

注意:

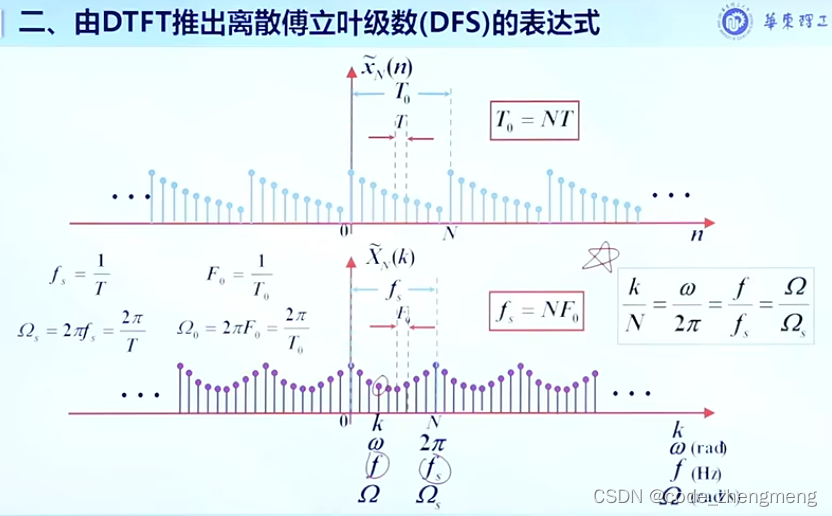
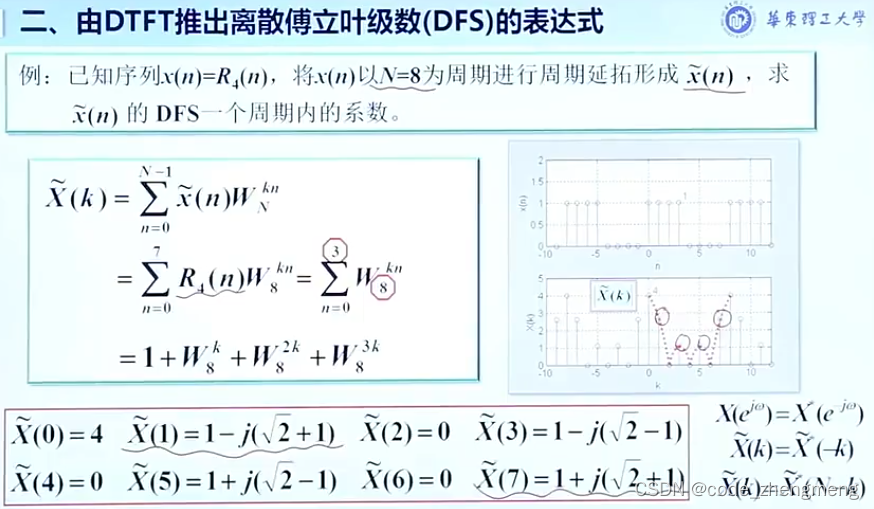





DFT和DFS的关系:DFS是周期离散的,DFT是DFS的一个主值区间。
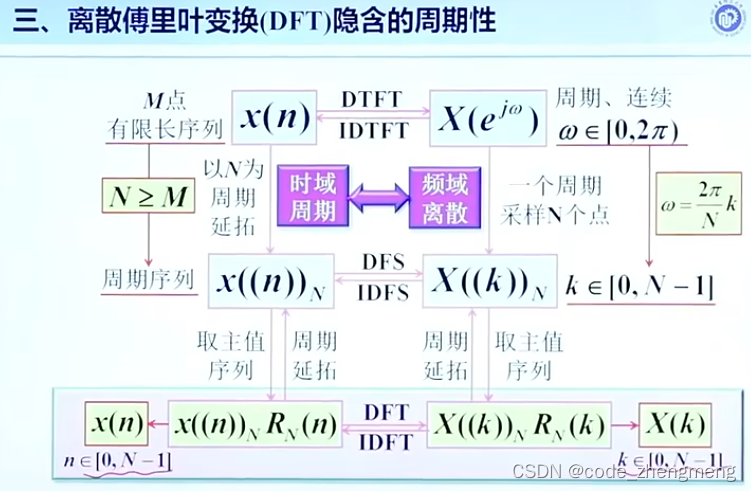


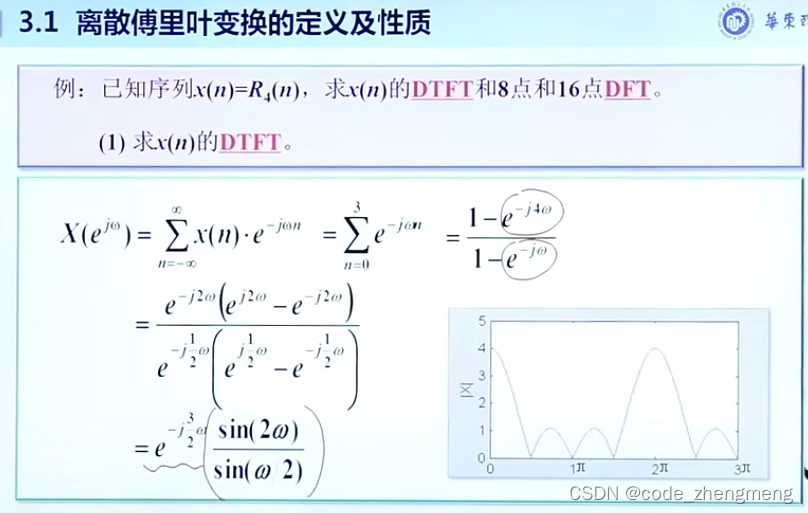
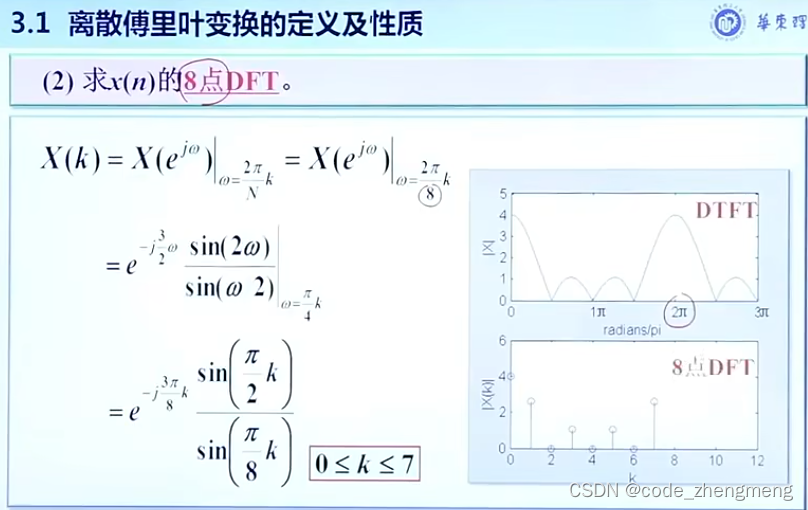





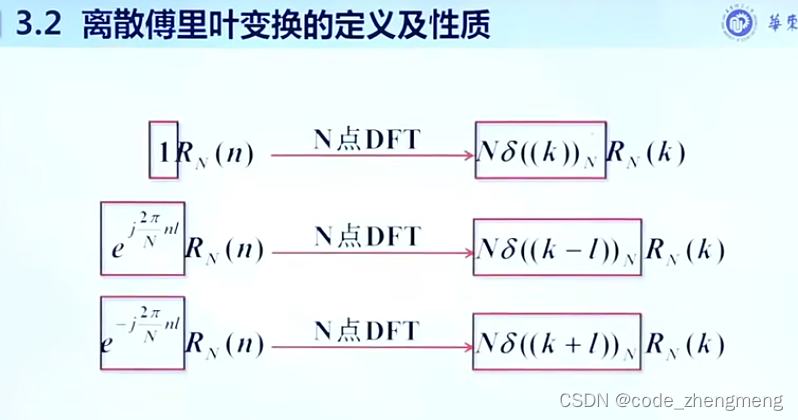


定理:




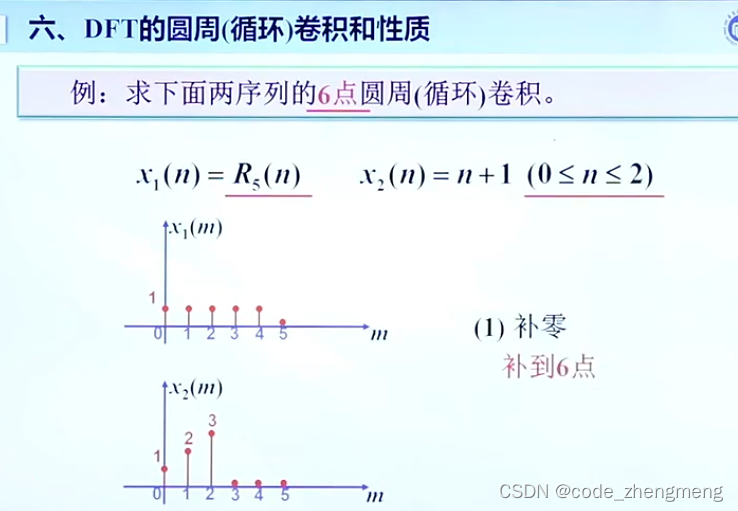
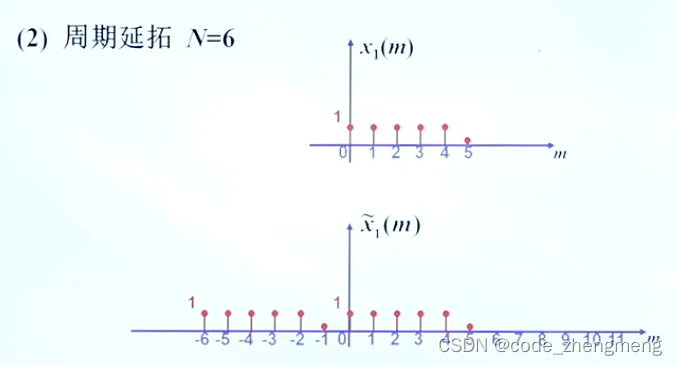
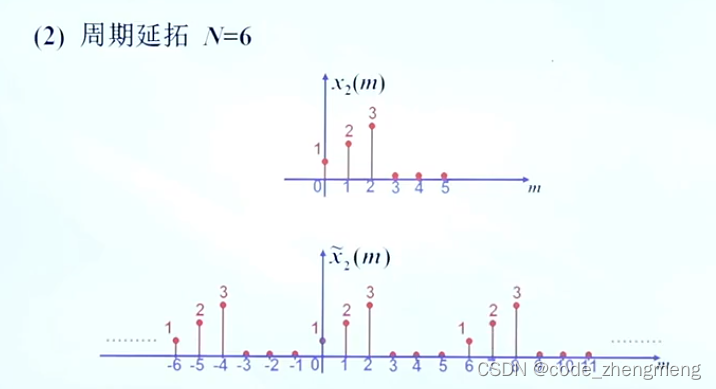









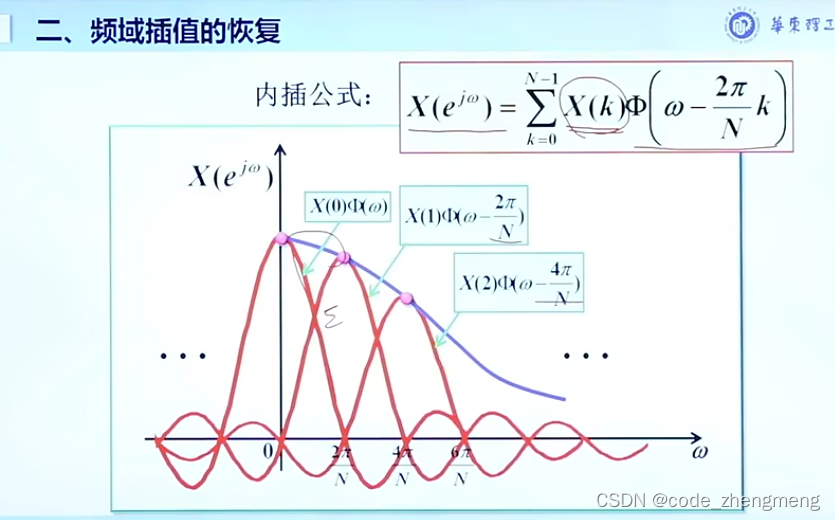

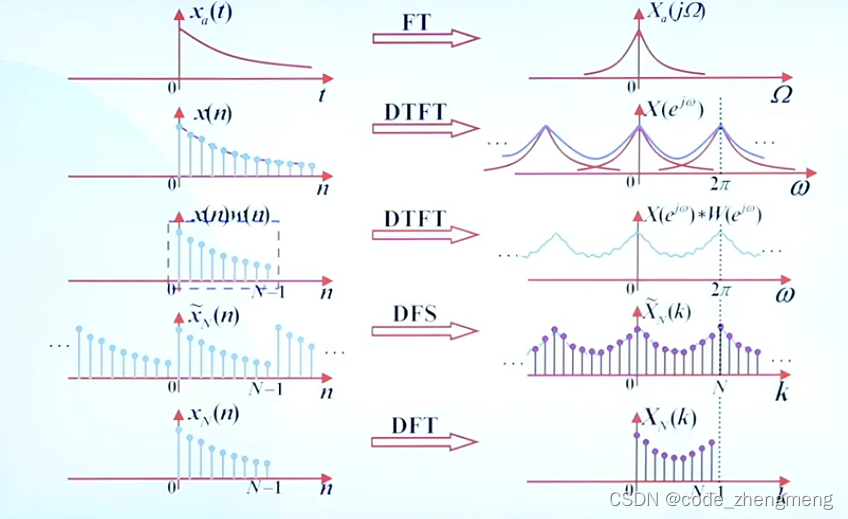




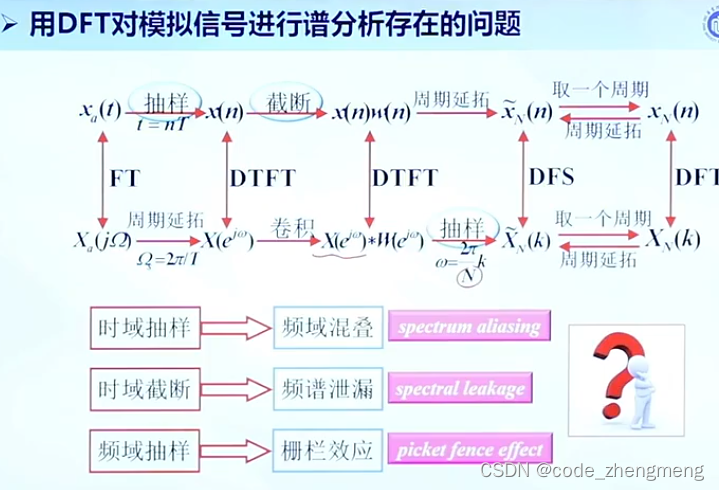
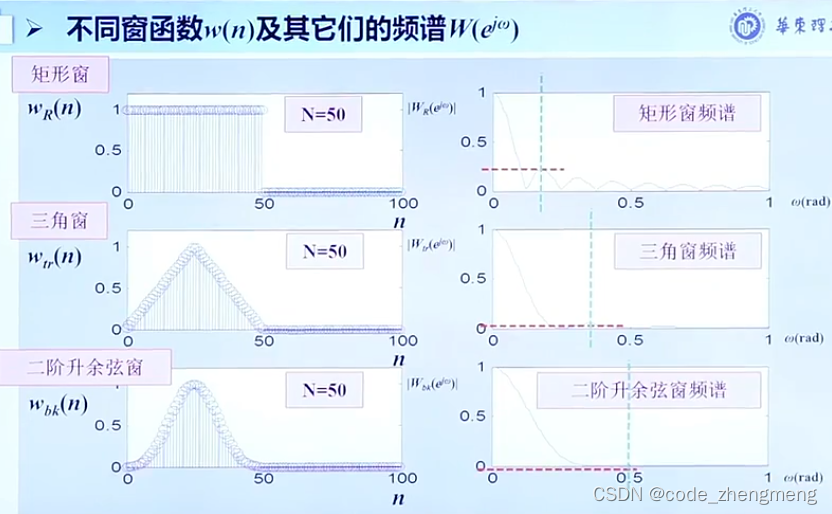
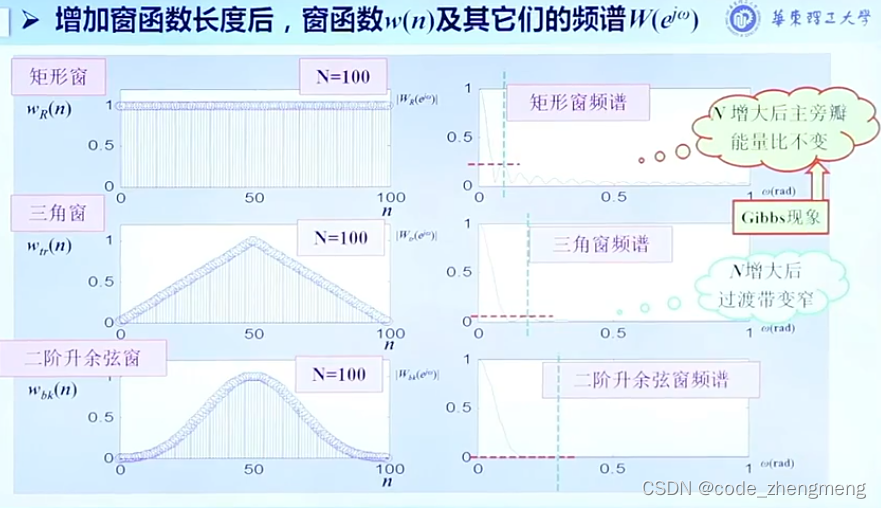



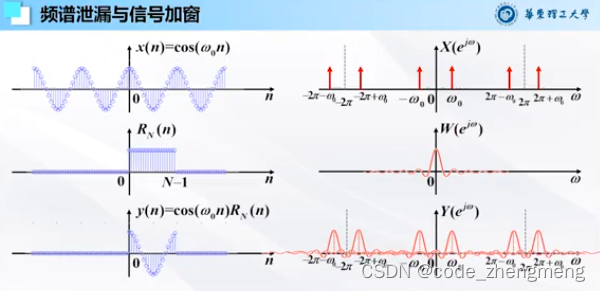
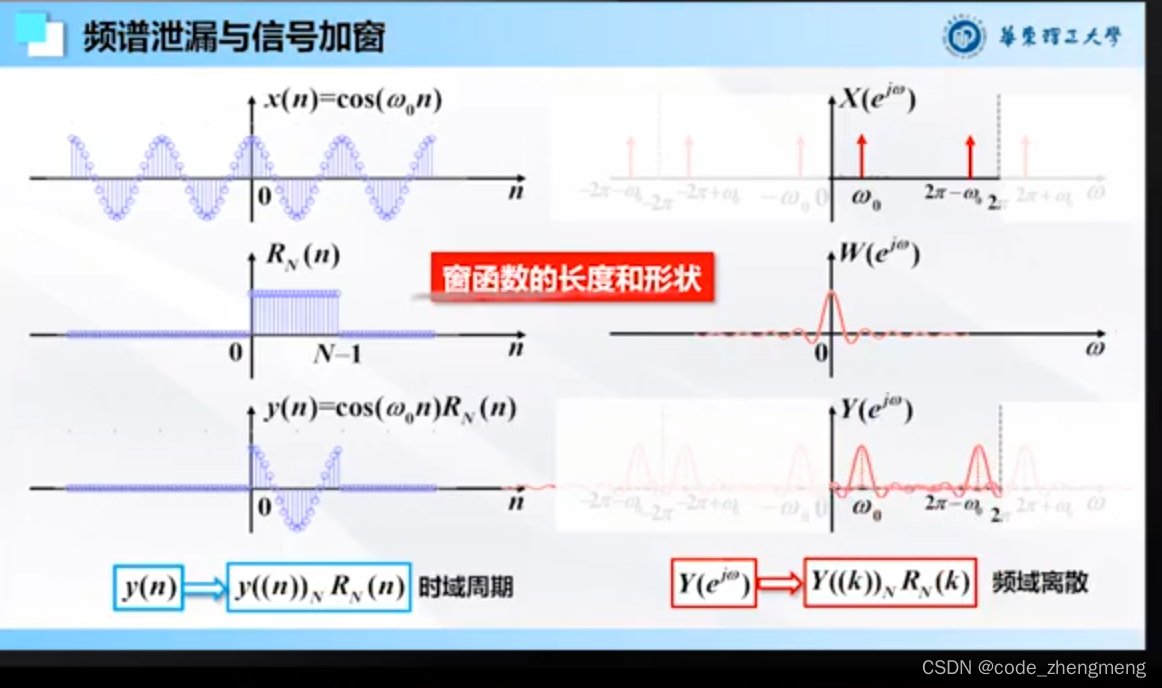


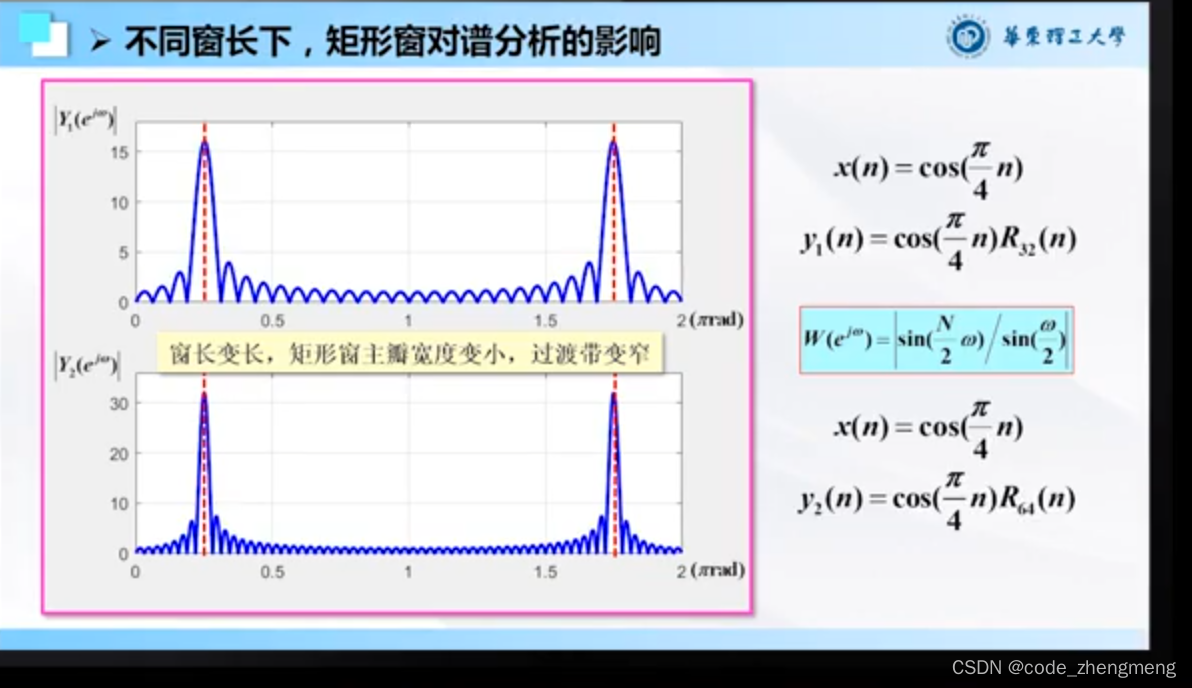
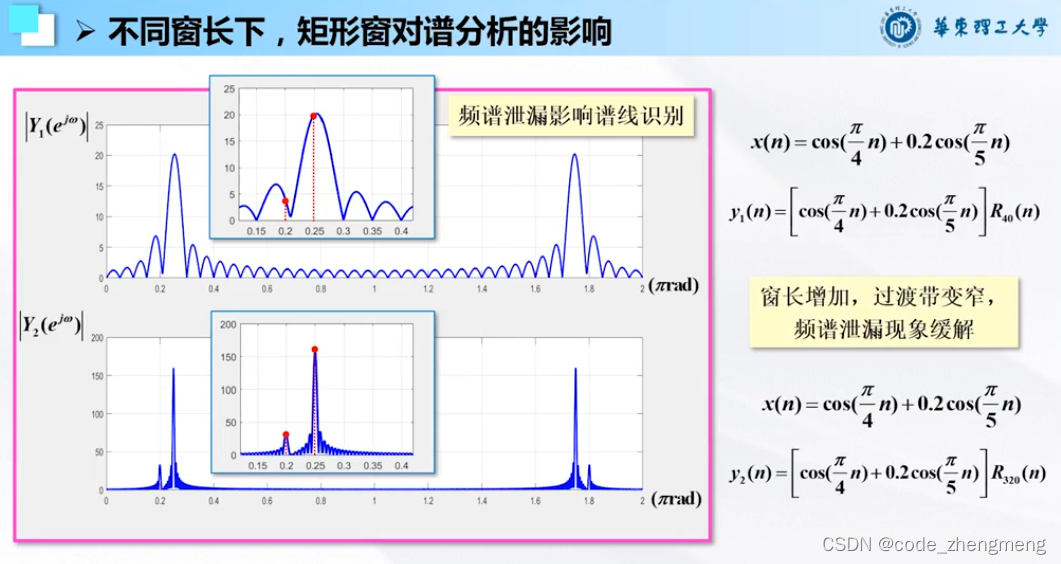
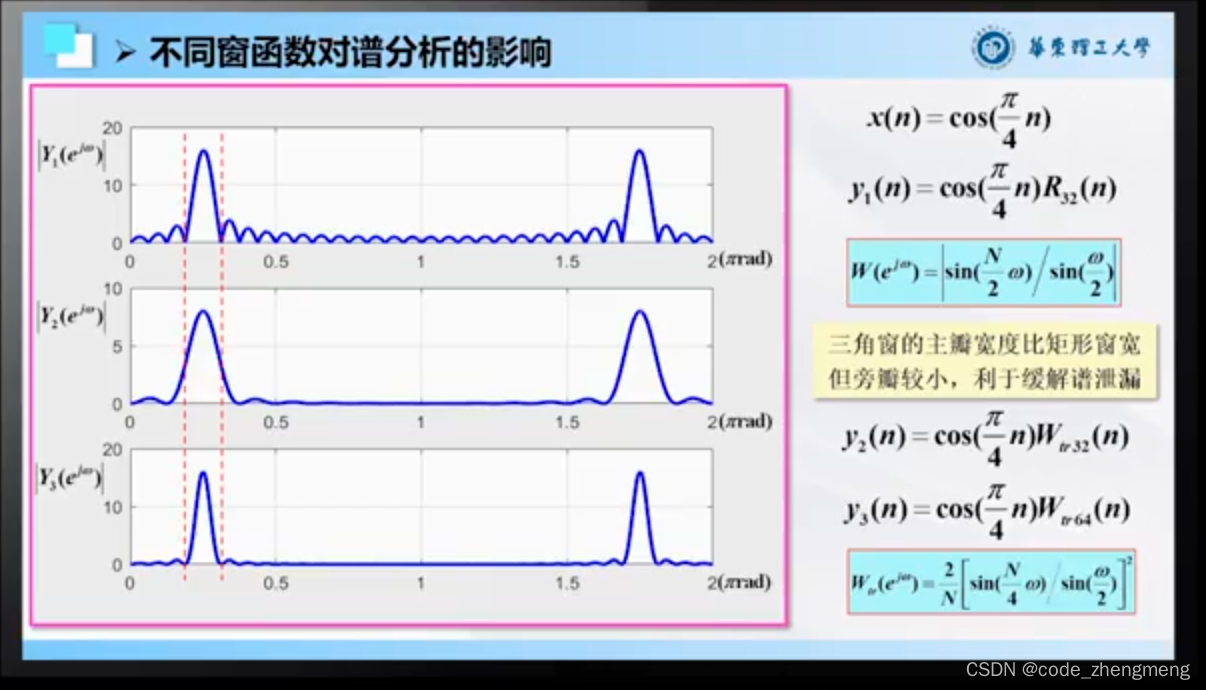

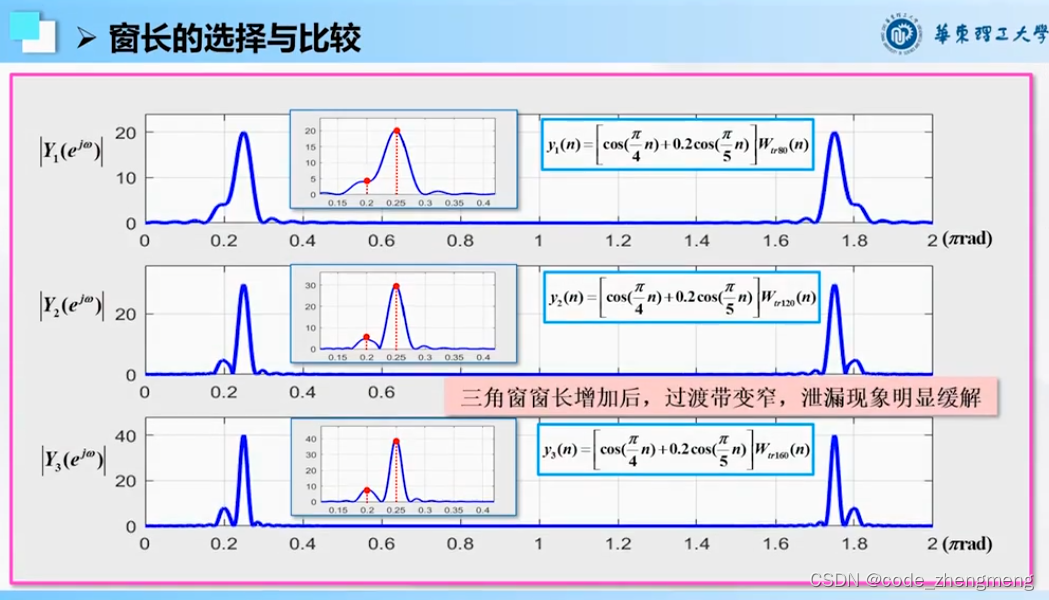
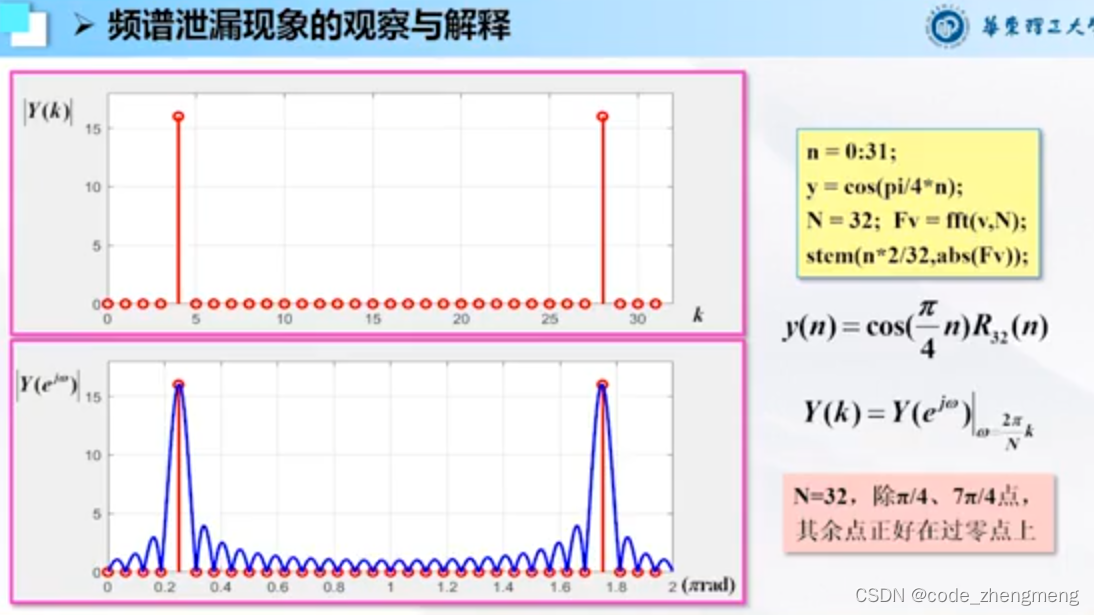
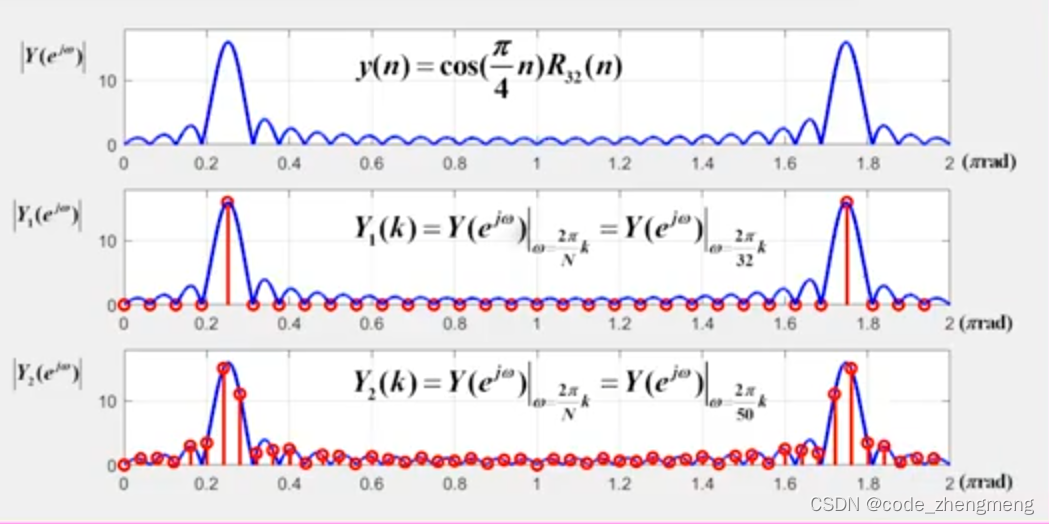
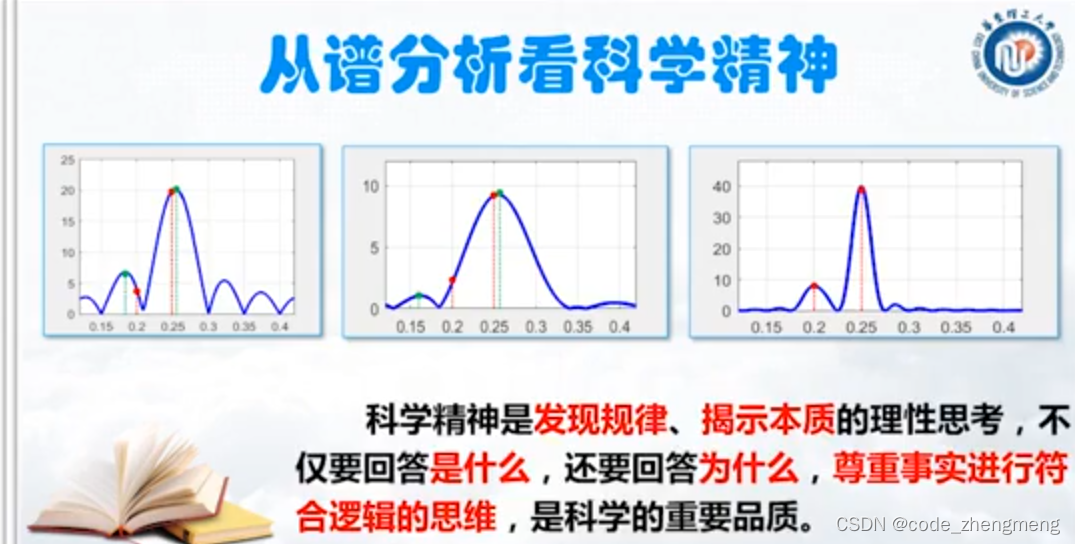
FFT变换


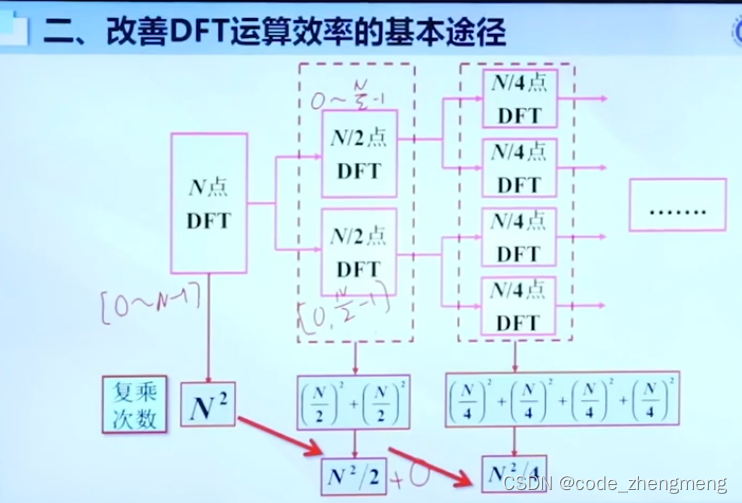


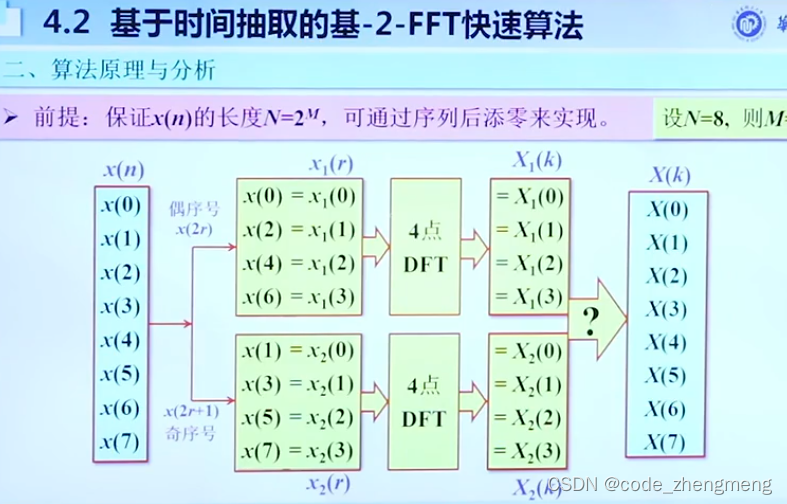



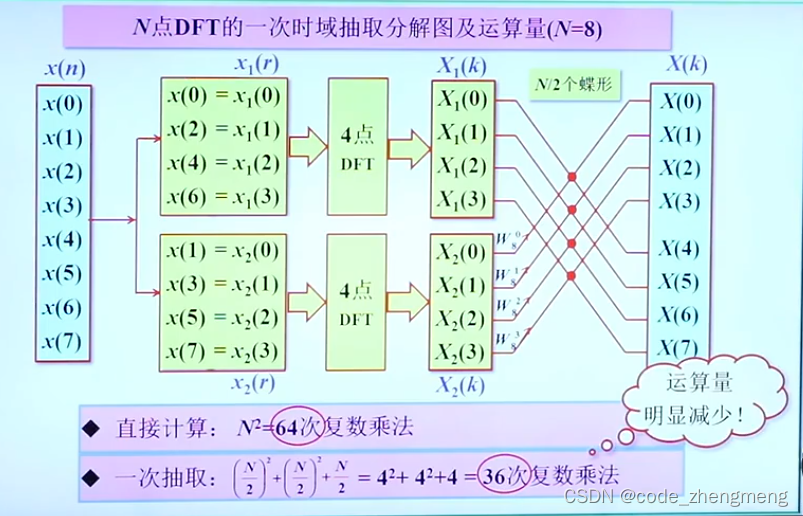



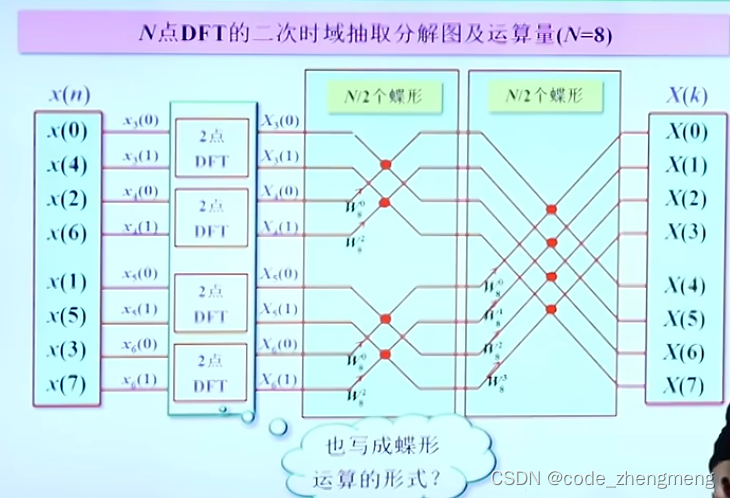

下图PPT公式写的不好,是,下面同理
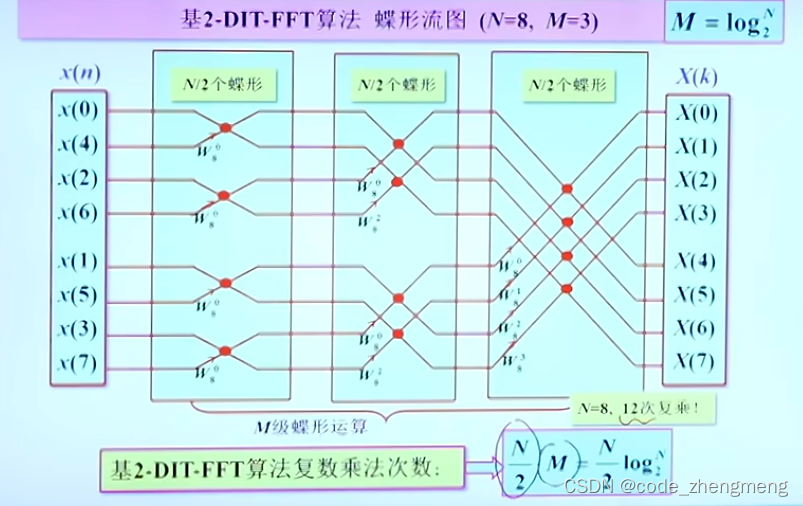




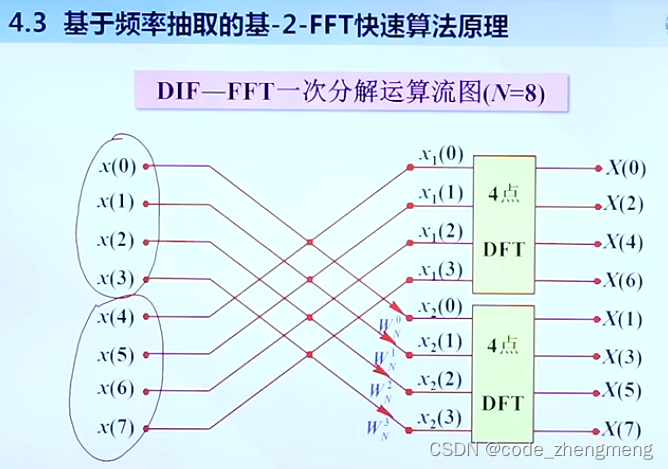



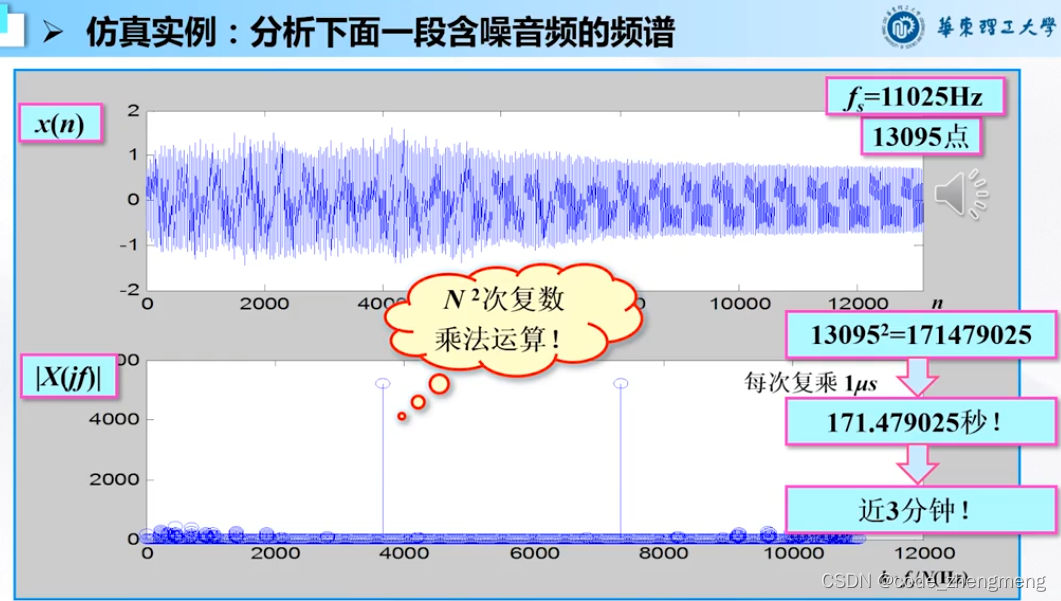
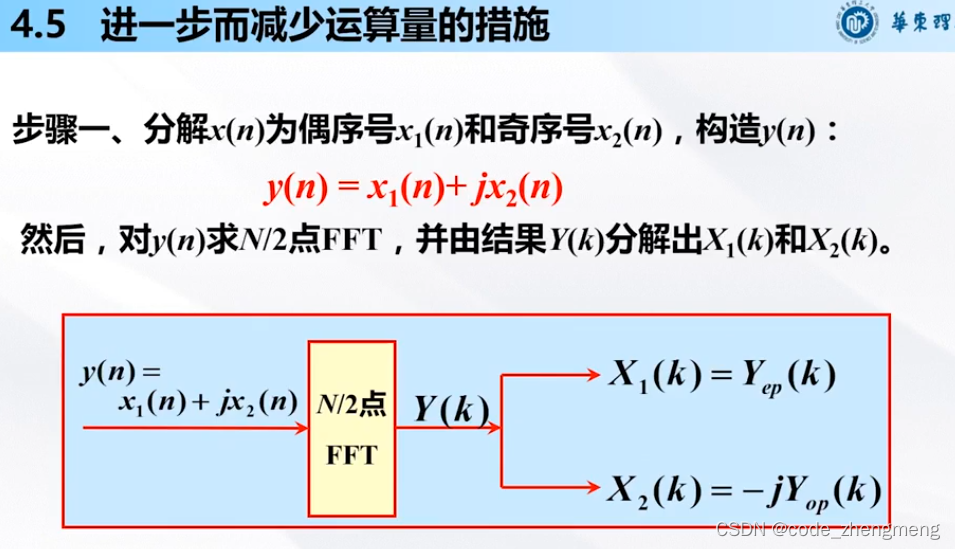
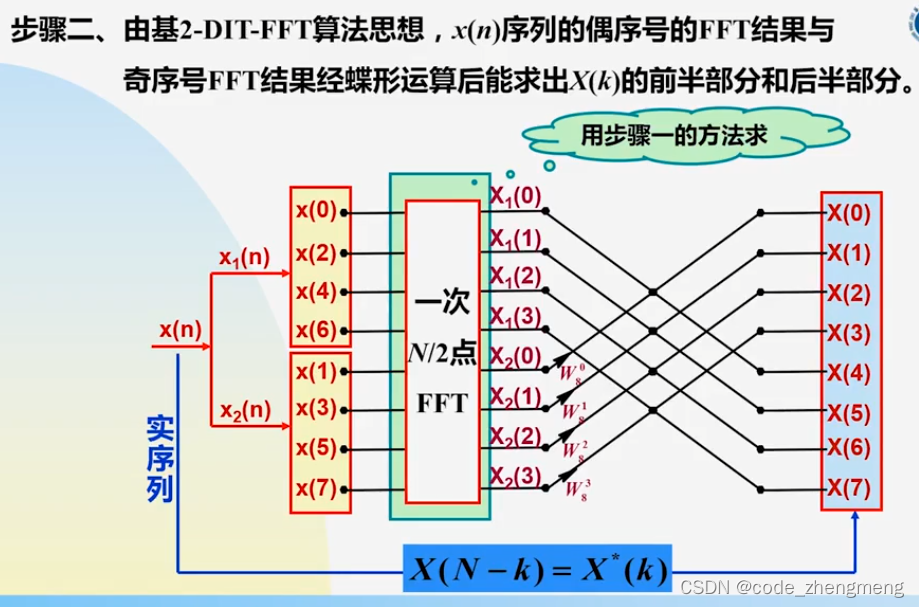
进一步提高计算速度的方法

























 111
111

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








