从Logistic回归到神经网络的一点感悟

从Logistic回归到神经网络的一点感悟

• 第一次写博客，是自己刚迈入新的学习节奏，想写一点东西，整理一下思绪的时候；也希望为数据分析学会的每周技术帖分享起个头。
• 主要是记录自己的感悟，当做学习笔记来写；有错误的地方欢迎指正。

---

1 线性回归 (Linear Regression)

大略总结下

回归来源

我们关心的东西没有办法用一个或多个变量确定的表示，即无函数关系；但是又存在着较强的关联性。这种关系就叫统计关系或相关关系。衍生两个分支是回归分析和相关分析。二者侧重不同，回归分析用的更广泛。
回归分析中，x称为解释变量，是非随机变量；y称为响应变量，是随机变量。
回归有线性回归和非线性回归；以最小二乘法(Least Square)为主的线性回归是最经典的回归模型。
回归和分类的问题是相同的，仅区别于响应变量的形式。y是分类变量时(例：0-1），模型为分类；是连续变量时称为回归。

线性回归总结

Gauss-Markov 假设：

高斯-马尔科夫是核心假设，后面回归出现的问题都由此而来。

1. 线性模型成立 $y =\beta_0 + \beta_1x_1 +...+ \beta_px_p +\epsilon$ , $\beta$是常系数，$\epsilon$是随机误差项。
2. 样本(sample) 是随机抽样得到。
3. 解释变量不为常数，没有共线性（一个变量不能由其他变量线性表示）
4. 误差项不相关：$Cov(\epsilon_i ,\epsilon_j) =0 , 0\leq i,j \leq n$
5. 误差项同方差: $Var(\epsilon_i) =\sigma,i=1..n,\sigma$是常数。

常见问题及解决办法

• 异方差性：即GM假设第5条不满足，$\sigma_i$不再是常数。解决办法：加权最小二乘。打个广告，解决异方差性，这篇推送写的不错：如何收服异方差性

• 多重共线性：第3条不满足。举例：自变量同时有一天进食量和中午以后进食量。解决办法：根据多重共线性检验删除一些不重要的变量；逐步回归、主成分回归、偏最小二乘，Ridge,Lasso（岭回归与LASSO为正则化方法，在解释性上强于前面两种）
  

• 当响应变量是定性变量。解决办法：

  • 在数据处理上设置哑变量(dummy variable)
  • 响应变量是定性变量在生活中有广泛的应用，其属于广义线性模型(generialized linear model,GLM)的研究范畴。

2 感知机 (Perceptron)

定义

当响应变量 $y$ 是分类变量时，建模过程就是分类了。感知机(Perceptron)是二分类的线性分类模型。可以看做是线性回归的兄弟（线性分类)。同时也是神经网络和支持向量机(support vector machine)的基础。
下一篇学习笔记会试着写写从感知机到支持向量机。

在周志华老师的机器学习一书中侧重于将其作为神经网络的基础概念，对感知机的定义如下：

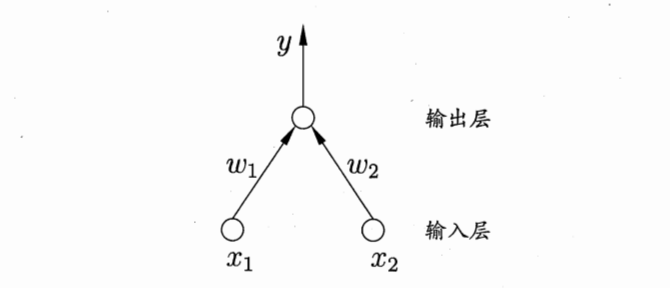
感知机由两层神经元组成，输入层接受外界输入信号后传递给输出层，输出层是M-P神经元，亦称“阈值逻辑单元”(threshold logic unit)。如下图所示：

学习策略

在感知机模型中，假设数据集是线性可分的。因此，感知机的目标是找到一个超平面，将两类点(正 or 负)完全分隔开来。因此，学习策略的核心是找到这样的超平面方程：$wx + b =0$

因此，训练需要得到的参数是 $w$ 和 $b$。采用误分类点到该超平面的距离来作为损失函数；这里不选误分类点的总个数是因为这样的损失函数不是参数 $w$ 和 $b$的连续可导函数，不便于优化。

损失函数：

$L(w,b)= -\sum_{x_i \in M} y_i(w\cdot x_i + b)$
其中 $M$是误分类点的集合。这个损失函数就是感知机学习的经验风险函数；所以问题就转化为一个求解损失函数最小的最优化问题，最优化的方法是随机梯度下降(Stochastic gradient descent)。对于更多细节可以看李航的统计学习方法这本书；感知机这部分在书中有很全面的介绍。

3 Logistic Regression

怎么来的

在前面已经提到了广义线性模型，其一般表示形式为：

y=g−1(wTx