论文阅读笔记《Learning Visual Servoing With Deep Features and Fitted Q-Iteration》

核心思想

  该文提出一种基于深度特征和Fitted Q-Iteration（FQI）的学习型视觉伺服算法，相对于使用图像中人为设计的特征，深度特征具备更强的鲁棒性，能够更好的应对图像中光照、角度变化、遮挡等问题的影响。但使用深度特征同样也带来了一些问题，比如深度特征维度比较高，如何从中选择有用的特征信息；深度特征描述了整幅图像的情况，如何从中定位出感兴趣区域或者目标。该文通过FQI算法为深度特征的每个通道都赋予一定的权重，通过权重的大小来选择出最有用的特征信息。
  首先，要利用一个卷积神经网络从图像中提取出深度特征信息，本文选择了在ImageNet预训练得到的VGG网络，并且使用空洞卷积取代了普通卷积和最大池化层，经过特征提取后得到32 * 32大小的特征图，网络结构如下

  提取的特征信息经过下采样后可以得到多尺度的特征信息$y_t^{(l)}$。提取的多尺度特征信息被用来预测下一时刻的特征$y_{t+1}^{(l)}$，这个预测过程作者采用了一个双线性模型$f^l$，输入当前时刻的多尺度特征信息$y_t^{(l)}$和当前时刻的控制指令$u_t$，输出下一时刻的特征信息${\hat{y}}_{t+1}^{(l)}$。如果采用全连接的双线性模型，就是输出特征图中每个像素的特征值都于输入特征图的特征值有关，则会使整个模型的参数变得巨大，因此本文采用了局部链接的双线性模型，这个改变可以参考卷积神经网络和全连接网络的区别。模型的计算过程如下

其中$W_{c,j}^{(l)}$和$B_{c,j}^{(l)}$分别表示对应尺度$l$上通道$c$中位置$j$处的权重和偏置参数。训练过程也非常简单，使用$l_2$损失函数来度量预测特征${\hat{y}}_{t+1}^{(l)}$和真实特征$y_{t+1}^{(l)}$之间的差距，并采用Adam算法反向传播损失更新参数。整个过程如下图所示

图中$h$表示VGG特征提取网络，$d$表示下采样网络，$f$表示双线性模型
  得到深度特征信息后，就要计算控制策略了。最优控制策略的思路就是，寻找一种控制指令使得下一个时刻的深度特征信息与期望位置的深度特征信息$y_{\ast ,c}^{(l)}$差距最小，计算过程如下所示

其中$\left|y_{\cdot ,c}^{(l)}\right|$表示特征误差的归一化系数项，$w_c^{(l)}$表示第$l$个尺度下，第$c$个通道的权重值，并且使用离散权重${\lambda }_j$对每个位置处的控制指令$u_j$进行加权。优化的目标就是寻找这个最优的控制指令$u$，使用Q值函数来近似上述的优化目标的话可得

其中参数${\theta }^T=\left[\begin{array}{cc}{w}^T& {\lambda }^T\end{array}\right]$并且增加了一个偏置参数$b$，$s_t=(x_t,x_{\ast })$表示当前时刻和期望位置的状态，则伺服控制策略可以简单写为

  下面的问题就是如何使用基于强化学习，具体来说是采用FQI的方法来优化参数$\theta$，进而去计算最优的控制指令$u$。强化学习的训练目标是最小化Bellman损失函数

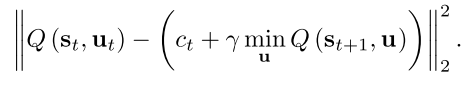
其中$c_t$表示$t$时刻执行动作后获得的奖励，对于FQI算法，训练阶段需要对每个时刻的每个样本都采样得到以下信息${\left\{s_t^{(i)},u_t^{(i)},c_t^{(i)},s_{t+1}^{(i)}\right\}}_i^N$作为训练集。可以看到损失函数中同时包含当前时刻和下一时刻的Q值函数，如果同时对两个函数进行优化是很困难的，因此通常会先固定其中一个Q值函数不变，优化另一个的Q值函数，然后依次迭代优化两个函数。作者发现当给定状态$s_t$时，对于任何带有非负系数$\alpha$的参数$\theta$和任何的偏置参数$b$，其能够最小化Q值的动作都是一样的。因此在第$k-1$次迭代和第$k$次迭代之间增加了一个步骤，被称为第$k-\frac{1}{2}$次迭代，在这一步中先对参数${\alpha }^{(k-\frac{1}{2})}$和$b^{(k-\frac{1}{2})}$进行优化，计算过程如下

最后一项是正则化项。然后参数$\theta$可以更新为${\theta }^{(k-\frac{1}{2})}={\alpha }^{(k-\frac{1}{2})}{\theta }^{(k-1)}$，然后再在${\theta }^{(k-\frac{1}{2})}$和$b^{(k-\frac{1}{2})}$的基础上在更新得到${\theta }^{(k)}$和$b^{(k)}$，过程如下

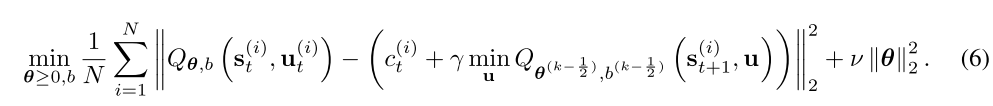
整个FQI过程的伪代码如下

算法评价

  本文首先是使用深度特征信息取代了人为设计的图像特征，这增加了特征的鲁棒性。而得到特征信息如何使用，并计算得到相应的控制律，本文则是提出了基于强化学习FQI的方法。并且在实现过程中提出了局部链接双线性模型和分阶段的迭代优化策略来提高算法的执行效率。

如果大家对于深度学习与计算机视觉领域感兴趣，希望获得更多的知识分享与最新的论文解读，欢迎关注我的个人公众号“深视”。