泰勒展开式记忆方法

原创已于 2023-07-18 10:37:04 修改

· 4.8k 阅读

·

7

·

版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

#高等数学 #泰勒 #泰勒展开式

于 2022-11-05 19:17:27 首次发布

泰勒认为“仿造一段曲线，要先保证起点相同，再保证在此处导数相同，继续保证在此处的导数的导数相同……”

一、简介

泰勒公式，也称泰勒展开式。是用一个函数在某点的信息，描述其附近取值的公式。如果函数足够平滑，在已知函数在某一点的各阶导数值的情况下，泰勒公式可以利用这些导数值来做系数，构建一个多项式近似函数，求得在这一点的邻域中的值。

关于多项式，它本身的运算是有限项的加减法和乘法，因此泰勒思考，能否用多项式函数去近似表达给定的函数。我们期望两个函数在某一点的函数值、一阶导数值、二阶导数值等相等，因为这些值表达了函数图像最基本和最主要的性质，这些性质的逼近可以使得两个函数图像逼近。

余项，即为误差，我们使用多项式函数在某点展开，逼近给定的函数，但是最后肯定会有一点点误差。

二、常见泰勒展开式

1、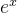 $e^{x}$

$e^{x}=1+x+\frac{x^{2}}{2!} +\frac{x^{3}}{3!} +... +\frac{x^{n}}{n!}$

对两边进行求导

$(e^{x})'=(1+x+\frac{x^{2}}{2!} +\frac{x^{3}}{3!} +... +\frac{x^{n}}{n!})'$

求导得：

$e^{x}=0+1+\frac{x}{1}+\frac{x^{2}}{2!} +\frac{x^{3}}{3!} +... +\frac{x^{n}}{n!}$

两边都不改变，并且满足 $e^{0}=1$

2、 $a^{x}$

将 $x$ 换成 $x\ln a$ ，带入上面的公式：

$a^{x}=e^{x\ln a}=1+x\ln a+\frac{(x\ln a) ^{2}}{2!} +\frac{(x\ln a)^{3}}{3!} +... +\frac{(x\ln a)^{n}}{n!}$

3、 $\sin x$

$\sin x$ 为奇函数，只有奇数项，并且 $\sin 0=0$ ，x的次方数也为奇数项，符号正负交替

$\sin x=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}...+\frac{(-1)^nx^{2n+1}}{(2n+1)!}$

4、 $\cos x$

我们可以发现， $\sin x$ 的求导就是 $\cos x$

$\cos x$ 为偶函数，只有偶数项，并且 $\cos 0=1$ ，x的次方也为偶数项，符号正负交替

$\cos x=1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}...+\frac{(-1)^nx^{2n}}{(2n)!}$

5、 $\ln (1+x)$

记忆：无阶乘，符号正负交替

$\ln (1+x)=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}+...\frac{(-1)^nx^{n+1}}{n+1}$

6、 $\tan x$

默默地记住它...

$\tan x=x+\frac{x^{3}}{3}+\frac{2x^{15}}{15}+\frac{17x^{315}}{315}+...$

7、 $\arctan x$

$\arctan x =x-\frac{x^{3}}{3}+\frac{x^{5}}{5}+...$

8、 $\arcsin x$

$\arcsin x=x+\frac{x^{3}}{6}+...$

9、最后的汇总

注意：使用泰勒展开式时要注意分子分母同阶

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。