奇偶性

最新推荐文章于 2022-11-05 19:17:27 发布
最新推荐文章于 2022-11-05 19:17:27 发布
阅读量1w 收藏 7
点赞数 4
分类专栏： 数学
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/zy19991023/article/details/116533651
版权
本文探讨了数学中函数的奇偶性及其与导数的关系，证明了奇函数的导数是偶函数，偶函数的导数是奇函数，但反向推断并不总是成立。此外，还解释了连续奇函数和偶函数的原函数性质，并通过泰勒展开式展示了奇偶性如何帮助解题。同时，提到了反函数的存在性和单调性的关系，并给出了一个分段函数的例子来说明。
摘要由CSDN通过智能技术生成

奇偶性

f（x）奇函数 => f'(x)偶函数   但反之不成立 如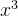x^{3}+1的导数3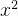x^{2}偶函数 推不出原函数奇函数

f（x）偶函数 <=> f'(x)奇函数

证明：法一：f(x) 奇函数 则f(-x)=-f(x) 对上式求导得 -f'(-x) = -f'(x)  所以 f'(-x)=f'(x) 偶函数

f(x)偶函数 则f(x)=f(-x) 求导得 f'(x) = - f'(-x) 奇函数

法二：导数定义 

f'(x)= \lim_{\Delta x \to 0}\frac{f(-x+\Delta x)-f(-x)}{\Delta x} = \lim_{\Delta x \to 0}\frac{-(f(x-\Delta x)-f(x))}{\Delta x}=\lim_{-\Delta x\rightarrow 0}    =f'(-x)

原函数的问题

连续的奇函数的原函数都是偶函数，连续的偶函数的原函数之一是奇函数

为什么要连续？考虑变上限积分函数\int_{a}^{x}f(t)dt 对其求导可得f(x)

f(x)奇函数 则 \int_{0}^{x}是偶函数 再加上c也是偶函数

f(x)偶函数 \int_{0}^{x}是奇函数 ，在0处必为0 不能加c

奇偶性可以帮助解题

常见的奇函数ln\frac{1-x}{1+x}，ln(x+\sqrt{1+x^{2}}),\frac{e^{x}-1}{e^{x}+1}

如f(x)=\frac{sinx}{1+x^{2}} 是奇函数，求x=0处的三阶泰勒展开为ax+bx^{2}+cx^{3}

可知b一定为0

结论：偶函数泰勒展开只有偶次项 ，奇函数泰勒展开只有奇次项

关于反函数

原函数单调，必有反函数，反之，有反函数不一定单调

分段函数f(x)=x (0<x<1) 3-x ([1,2]) 

hao-zhuang
关注
  • 4
    点赞
  • 踩
  • 7
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
高等数学精讲01 第一章第一节 函数
猫宁的博客
05-13 4104
第一章 函数，极限，连续 概要： 函数：高等数学研究的主要对象 极限（重点难点）：用来研究函数的工具，重要概念都是极限用来定义的，连续，导数，定积分 连续性：研究的第一个基本形态 第一节 函数 主要内容： 函数的概念以及一些常见的函数 函数的四大基本性态 考卷考题： 题型一：复合函数 题型二：函数性态（每年必考，分值很高） 一、函数概念以及常见函数 1.函数的概念 不提值域是因为，得到定义域和对应法则就可以去确定值域 2.复合函数 复合函数的关键是看外层函数的定义域和内层函数的值域是否有交集 3.
高等数学精讲05 第一章第三节 连续
猫宁的博客
05-25 1243
题型三、已知极限，确定参数 方法一、个个击破，使用提取无穷因子的方法 除以0，极限为0，个个击破 题型四、无穷小量阶的比较 1、洛必达法则 2、等价无穷小替换 3、泰勒公式 低阶无穷小+高阶无穷小=低阶无穷小 多项式去定义一大堆系数，传统方法使用泰勒 偶函数的零点展开式只可能是偶次项，所以n不可能是奇数 第三节 连续 考点概要 一、连续的概念 二、间断点及其分类 三、连续函数的性质 常见考题 题型一、讨论连续性及间断点的类型 讨论间断点对函数做变形，一定要考虑到.
泰勒展开式记忆方法
weixin_51293984的博客
11-05 3808
x的次方数也为奇数项，符号正负交替。x的次方也为偶数项，符号正负交替。为奇函数，只有奇数项，并且。为偶函数，只有偶数项，并且。记忆：无阶乘，符号正负交替。两边都不改变，并且满足。
第一章____函数、极限、连续
qq_36323561的博客
03-20 6360
n项和极限的求法 目前为止（至定积分），仅有两种算法 ① 夹逼定理 ② 定积分定理 关于两种方法的选择： 一般考虑这两类方法的题目都是带有分母的题，可将分母分成主体部分和变体部分 lim⁡n→∞变体部分主体部分=A(≠0)\lim_{n\to \infty}\frac{变体部分}{主体部分}=A(\neq0)limn→∞​主体部分变体部分​=A(​=0) 两部分为同量级 用定积分定义 lim⁡n→∞变体部分主体部分=0\lim_{n\to \infty}\frac{变体部分}
高数强化 第一章 函数、极限、连续 (一)
m0_65207522的博客
10-02 1023
高数强化 第一章 函数、极限、连续 (一)
数字筛选，奇偶性归类区分
04-16
本主题“数字筛选，奇偶性归类区分”关注的是如何使用编程语言，如Java，来实现这个功能。我们将深入探讨相关的知识点，包括数据类型的处理、条件判断、数组操作和排序算法。 首先，我们要理解Java中的数字类型，...
从键盘任意输入一个整数，编程判断它的奇偶性。要求输入变量定义为int类型且由用户从键盘输入。
01-12
从键盘任意输入一个整数，编程判断它的奇偶性。要求输入变量定义为int类型且由用户从键盘输入。
中职数学函数奇偶性PPT课件.pptx
10-11
中职数学函数奇偶性PPT课件 本PPT课件主要针对中职学生，讲解函数奇偶性的概念和性质，通过多种图形和公式，帮助学生理解和掌握奇函数的定义、图象特征和判断方法。 函数奇偶性定义 奇函数是指对于函数y = f(x)的...
中职数学函数的奇偶性说课PPT课件.pptx
10-11
中职数学函数的奇偶性说课PPT课件 本资源是一份中职数学函数的奇偶性说课PPT课件，共20页，主要内容包括学情分析、教学策略、教学过程、教学反思等方面的内容。 首先，在学情分析中，作者介绍了学生的文化基础薄弱...
python 给你一个正整数列表 L, 判断列表内所有数字乘积的最后一个非零数字的奇偶性。如果为奇数输出1,偶数则输出0。
11-21
# 结尾非零数的奇偶性 # 给你一个正整数列表 L, 判断列表内所有数字乘积的最后一个非零数字的奇偶性。如果为奇数输出1,偶数则输出0。 # 输入示例 # 输入：L=[2,8,3,50] # 输出示例 # 输出：0 # 解析 # 在上题的基础...
泰勒公式推导过程_浅谈泰勒展开的巧记及其唯一性的妙用（1）
weixin_39995439的博客
11-23 7074
本文全部内容均转载自作者的公众号【数理tricks】生活不可万事都硬刚，学术也一样~ 在物理学习中常用到泰勒展开做局域的近似计算或直接作为考察某些物理过程的研究方法（正如热学中可逆过程既可作为真实过程的近似，又是一些热学过程的研究手段），正因如此，泰勒展开在物理学研究中占有重要的地位，而若按照正常的算法，泰勒展开公式要做若干次求导运算，在绝大多数时候显得极其繁琐，此时我们便会想找一些更便捷的方法去...
常见泰勒展开公式及复杂泰勒展开求法
星辰火之梦
10-16 3万+
初等的函数泰勒展开 ex{e^x}ex ex=1+x+12!x2+13!x3+...+1n!xn+o(xn){e^x} = 1 + x + {1 \over {2!}}{x^2} + {1 \over {3!}}{x^3} + ... + {1 \over {n!}}{x^n} + o({x^n})ex=1+x+2!1​x2+3!1​x3+...+n!1​xn+o(xn) sin⁡x\sin xsinx sin⁡x=x−13!x3+15!x5−...+1(2n+1)!x2n+1+o(x2n+2)\sin x
python泰勒公式法求正弦函数_正弦函数两种泰勒展开式的比较
weixin_39626690的博客
12-19 2411
正弦函数两种泰勒展开式的比较张文华，汲守峰【摘要】摘要：讨论了正弦函数在两种不同情况下的泰勒公式展开式，并利用余项比较两种展开式在近似计算中误差的大小区别，解释了正弦函数展开式中经常展开偶数项而不是奇数项的原因.【期刊名称】赤峰学院学报(自然科学版)【年(卷),期】2018(034)012【总页数】2【关键词】正弦函数；泰勒公式；拉格朗日余项基金项目：唐山学院2017年教育科学研究项目(1703...
泰勒公式（泰勒展开式）通俗+本质详解
热门推荐
吴明磊的博客
03-03 47万+
比较通俗地讲解一下泰勒公式是什么。 泰勒公式，也称泰勒展开式。是用一个函数在某点的信息，描述其附近取值的公式。如果函数足够平滑，在已知函数在某一点的各阶导数值的情况下，泰勒公式可以利用这些导数值来做系数，构建一个多项式近似函数，求得在这一点的邻域中的值 所以泰勒公式是做什么用的？ 简单来讲就是用一个多项式函数去逼近一个给定的函数(即尽量使多项式函数图像拟合给定的函数图像)，注意，逼近的...
几个函数泰勒展开式及其记忆技巧
赵英超的博客
05-03 5万+
几个函数泰勒展开式及其记忆技巧。   
泰勒公式的展开细节解析（转载）
weixin_30940783的博客
05-01 4310
转载自：https://blog.csdn.net/dog250/article/details/76697167 上周写完了《《三体》读后思考-泰勒展开/维度打击/黑暗森林》后收到一些邮件，进一步思考了关于泰勒展开的意义。也许我掌握的那些网络技术比如Linux Netfilter，NAT之类，太过底层太过小众，所以大家几乎都是没有感兴趣的，倒是这种科普性质的文章和那些吐槽类的文章，会引...
关于函数泰勒展开的关键知识点深入分析
biao2488890051的博客
06-02 6298
泰勒展开必须展开到无穷项（就是为什么下面条件中要求的任意阶导数必须存在），累加求和才可以与f（x）精确相等，其要求的条件： 在x0点的任意阶导数都存在，注：导数等于0也是导数存在，如x^2任意阶导数就是存在的。x0点导数不存在指导数无穷大或者左右导数不相等。 那么f（x）就能精确相等的泰勒展开成如下式子： ，其中n趋于无穷大 严格展开成了上面的无穷项求和形式了，因此我们可以得到下面...
泰勒(Taylor)展开式
ma123rui的博客
10-11 5538
泰勒(Taylor)展开式（泰勒级数）
mjiansun的专栏
10-17 29万+
目录 泰勒公式 余项 1、佩亚诺(Peano）余项： 2、施勒米尔希-罗什(Schlomilch-Roche）余项： 3、拉格朗日（Lagrange）余项： 4、柯西（Cauchy）余项： 5、积分余项： 带佩亚诺余项 参考资料 泰勒公式 泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。 若函数f(x)在包含x0的某个...
Python奇偶性判断
最新发布
06-12
在 Python 中，判断一个数的奇偶性非常直观。通常有两种方法： 1. **使用取模运算符（%）**： 如果一个整数除以 2 的余数是 0，那么这个数就是偶数；如果余数是 1，则它是奇数。例如： ```python num = 5 if num % 2 == 0: print("Even") else: print("Odd") ``` 2. **使用 `isinstance()` 和 `math` 模块**： 如果你想确保输入的是一个整数，可以先检查类型，然后使用数学模块的 `is_even()` 函数（这个函数并不存在，但你可以自己定义一个这样的辅助函数）： ```python import math num = 7.5 if isinstance(num, int) and math.is_even(num): print("Even (assuming int and no float)") else: print("Odd or not an integer") ```
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值