2020考研数学一大纲之完全解析（四）

本节大纲内容

考试要求

1. 理解空间直角坐标系，理解向量的概念及其表示.
2. 掌握向量的运算(线性运算、数量积、向量积、混合积)，了解两个向量垂直、平行的条件.
3. 理解单位向量、方向数与方向余弦、向量的坐标表达式，掌握用坐标表达式进行向量运算的方法.
4. 掌握平面方程和直线方程及其求法.
5. 会求平面与平面、平面与直线、直线与直线之间的夹角.
6. 会利用平面、直线的相互关系(平行、垂直、相交等))解决有关问题.
7. 会求点到直线以及点到平面的距离.
8. 了解曲面方程和空间曲线方程的概念.
9. 了解常用二次曲面的方程及其图形，会求简单的柱面和旋转曲面的方程.
10. 了解空间曲线的参数方程和一般方程.了解空间曲线在坐标平面上的投影，并会求该投影曲线的方程.

考试内容

• 向量的概念

  

• 向量的线性运算，向量的数量积和向量积

  
  

• 向量的混合积

  定义：
  设 a ，b 与 c 是三个向量，(a x b) · c 称为三个向量a，b，c的混合积，记作[a b c]或[a,b,c]，即
  [a b c] = (a x b) · c = | a x b| |c| cos⁡β
  其中 β是向量 (a x b) 与 c 的夹角。
  先向量积后数量级，最终结果是一个实数。

  三向量的混合积的几何意义：

  它的绝对值 |(a x b) · c| 表示以a，b，c 为棱的平行六面体的体积。
  根据右手定则，确定混合积的符号。

  如果[a b c] = 0，即平行六面体的体积为零，也就是说 a，b，c 共面。由此可知三向量共面的充要条件是三向量的混合积为零。
  

  向量的混合积的运算性质：
  （1）(a,b,c) = (b,c,a) = (c,a,b). // 注意本性质的顺序性
  （2）(k a,b,c) = ( a,kb,c) = ( a,b,kc) = k( a,b,c).
  （3）(a1+a2,b,c) = (a1,b,c) + (a2,b,c)

• 两向量垂直、平行的条件

  （1）两个非零向量a与b平行的充分必要条件是 a = βb.
  （2）在坐标系下，两向量平行的充要条件是对应坐标成比例。
  （3）两向量垂直的充要条件是两向量的数量积为零，即 a · b = 0。
  （4）在坐标系下，两向量垂直的充要条件是用坐标运算等于零。
  

• 两向量的夹角

  利用向量的数积即可计算。
  

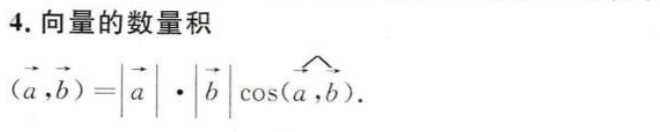
• 向量的坐标表达式及其运算

  

• 单位向量

（1）基本单位向量：针对坐标系来说的，坐标系正向的单位化 。
（2）非零向量a的单化：

• 方向数与方向余弦

  
  方向数和方向角是不同的。
  关于方向数：

• 曲面方程和空间曲线方程的概念

  

  建立了空间曲面及其方程的联系后，就可以通过研究方程来了解曲面的几何性质，与平面解析几何类似，空间解析几何主要研究两个基本问题：
  
  为了讨论方便，先简单介绍平面的一般方程
  空间中任一平面方程可以用三元一次方程
  
  来表示，反之亦然。其中A，B，C是不全为零的常数。此方程称为平面的一般方程。特别地，xOy、yOz、xOz平面的方程是z = 0，x = 0，y = 0。而x = c，y = c，z = c分别表示平行于坐标面yOz、xOz、xOy的平面。

常见曲面

• 球面

• 柱面

• 旋转曲面

• 常用的二次曲面方程及其图形

  点击下方常见曲面即可。
  常见曲面
  

• 空间曲线的参数方程和一般方程

  
  

• 空间曲线在坐标面上的投影曲线方程

  
  
  
  

  注意：投影曲线简称投影，而投影区域是投影曲线围成的区域。

• 平面方程

  
  

• 直线方程

  

• 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件

  
  
  （1）两平面垂直的充要条件是：法向量互相垂直。
  （2）两平面平行的充要条件是：法向量平行。
  （3）两直线垂直的充要条件是：方向向量垂直。
  （4）两直线平行的充要条件是：方向向量平行。
  （5）直线与平面平行的充要条件是：方向向量与法向量平行。
  （6）直线与平面垂直的充要条件是：方向向量与法向量垂直。

• 点到平面和点到直线的距离

补充

• 平面束方程