论文解读：（TransA）TransA: An Adaptive Approach for Knowledge Graph Embedding

论文解读：（TransA）TransA: An Adaptive Approach for Knowledge Graph Embedding

  先前的知识表示方法（TransE、TransH、TransR、TransD、TranSparse等）的损失函数仅单纯的考虑到 $h+r$ 和 $t$ 在某个语义空间的欧式距离，认为只要欧式距离最小，就认为 $h$ 和 $t$ 的关系为 $r$ 。显然这种度量标准过于简单，虽然先前的工作在得分函数上做出了不错的改进，但训练的损失函数制约了表示能力，因此，本文TransA模型的提出，主要对损失函数进行改进。
  虽然TransA的提出是在TransD、TranSparse之前，但实践表明TransA的提出很有价值。

一、简要信息

序号	属性	值
1	模型名称	TransA
2	所属领域	自然语言处理
3	研究内容	知识表示
4	核心内容	knowledge embedding
5	GitHub源码	https://github.com/thunlp/KB2E
6	论文PDF	https://arxiv.org/pdf/1509.05490.pdf)

二、摘要与引言

  知识表示在人工智能领域内是非常重要的任务，许多研究试图将知识库中的实体和关系表示为一个连续的向量。通过这些尝试，基于翻译模型的表示方法是通过最小化头实体到尾实体的损失函数。尽管这些策略非常成功，但其损失函数过于简单，不能够很好的表示复杂多变的知识图谱。为了解决这些问题，我们提出TransA，一种对表示向量的自适应度量方法。根据度量学习的想法提出一个更灵活的嵌入方法。实验在几个基线数据集上完成，我们的模型获得了最优效果。
  最近研究均涉及到知识图谱，像问答系统等需要对图谱进行表示，现如今提出的方法有TransE、TransH等。然而这些方法的度量标准仅仅是实体之间的欧氏距离，过于简单的损失函数不能够处理复杂多变的图谱。
（1）由于缺乏灵活的损失函数，当前的翻译模型均是应用球形等位超平面，因此越靠近中心，实体对与对应关系的向量越相似。如图所示，这是TransE模型在FreeBase上训练的向量通过PCA降维得到的图：

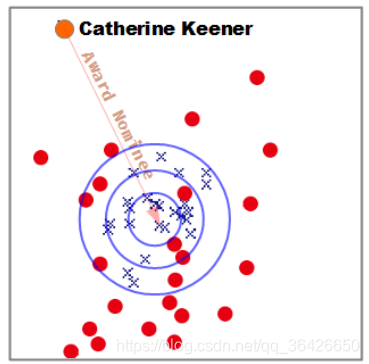
橘黄色的为头实体，橘黄色的线与箭头则为对应的关系向量。蓝色的叉表示正确的尾实体，红色的圆点则是错误的尾实体，可知当简单的使用欧式距离来评判，会掺和进大量错误的实体。由于图谱是复杂多变的，这一点很难避免。
（2）另外，由于过于简单的损失函数，使得当前几种翻译模型在对向量的每一个维度的训练处理方法相同。如图所示：

传统的方法采用欧氏距离度量实体对与关系向量的相似性（图（a）），假设这里向量只有两个维度 $x,y$ ，度量方法则是对 $x$ 和 $y$ 一样。然而当错误的实体（橘黄色空心圆）比正确的实体（橘黄色实心圆）更接近头实体与关系的和向量 $h+r$ （黑色圆表示头实体，箭头表示关系），则会预测错误。但是如果分别对不同维度进行考虑，如图（b），降低 $x$ 维度对度量的影响，提升 $y$ 方向对度量的影响，就可以让正确的尾实体“距离” $h+r$ 更近。这种度量不是传统的欧氏距离，而是马氏距离。

三、相关工作与主要贡献

  基于翻译模型：得分函数均为 $f_r(h,t)=||h_r+r-t_r|{|}_2^2$，但头尾实体的表示（语义空间）不同，分别如下：
（1）TransE：$h_r=h$，$t_r=t$；
（2）TransH：$h_r=h-w_r^{\mathbf{T}}h{w}_r$，$t_r=t-w_r^{\mathbf{T}}t{w}_r$ ；
（3）TransR：$h_r=M_{r}h$，$t_r=M_{r}t$ ；
（4）TransD：$h_r=M_r^{h}h$，$h_r=M_r^{t}t$ ；
  其他方法：
（1）非结构（UM）：与TransE相同，但所有关系 $r=0$ ；
（2）结构化（SE）：得分函数定义为 $f_r(h,t)=||M_{h,r}h-M_{t,r}t|{|}_2^2$ ；
（3）单层神经网络（SLM）：得分函数定义为 $f_r(h,t)=u_r^{\mathbf{T}}g(M_{r,1}h+M_{r,2}t)$ ；
（3）语义能量匹配（SME）：头尾实体分别与关系向量在一个全连接神经网络中计算后，相互乘积。

四、算法模型详解（TransA）

4.1 自适应度量分值函数

  作者认为传统的得分函数只是单纯的考虑向量之间的距离，对应超平面是一个球面，因此可能会将最近的错误的向量被预测为正确，因此提出一种新的得分函数为 $f_r(h,t)=(|h+r-t|{)}^{\mathbf{T}}{W}_r(|h+r-t|)$ ，其中 $|h+r-t|=(|h_1+r_1-t_1|,|h_2+r_2-t_2|,...)$，$W_r$是关系 $r$ 对应的非负加权矩阵。不同于传统的方法，得分函数使用绝对值，作者给出两方面的解释：
（1）一方面，只有在 $W_r$ 的所有项都是非负的情况下，绝对值计算才能使分数函数成为一个定义良好的范数；
（2）另一方面，忽略几何学中正负的方向性在TransA的应用。如果得分函数存在负数，如果其对应的权重过大，则损失函数便降低，然而负数并不能说明 $h+r$ 与 $t$ 的距离更近。

4.2 椭球面

  作者认为传统的方法是“球形等势面（Spherical Equipotential Surfaces）”的，何为球形等势面？由于传统的得分函数是欧式距离，$h+r$ 向量与 $t$ 向量存在一定的位移，当在训练过程中，一个 $h$ 可能与若干个 $t$ 存在 $r$ 关系，因此 $h+r$ 与 一定数量的 $t$ 之间的应保持较近距离，为了将所有正确的 $t$ 纳含进去，普通的得分函数就是在 $h+r$ 处画一个球面（二维空间中就是一个圆），并将所有正确的包含进去。但在所有正确的 $t$ 的范围内，总会存在错误的实体，因此保证查全率的情况下准确率非常低。如果选用 $f_r(h,t)=(|h+r-t|{)}^{\mathbf{T}}{W}_r(|h+r-t|)$ ，其对应的超平面由权重矩阵 $W_r$ 动态的控制，可能是一个球，也可能是压扁了的椭球，使得尽可能减少错误实体的条件下将所有正确的实体包含进去。

4.3 特征加权

  那权重矩阵 $W_r$ 如何计算？作者使用 LDL分解，即：$W_r=L_r^{\mathbf{T}}{D}_r{L}_r$ ，$L_r$ 是一种变换矩阵，$D_r=diag(w_1,w_2,...)$ 则是对角矩阵，$w_1,w_2$ 即为对应每个维度的权重。得分函数可写作：$f_r(h,t)=(L_r|h+r-t|{)}^{\mathbf{T}}{D}_r(L_r|h+r-t|)$ 。

4.4 实现细节

  采用距离排序损失函数，如图：

可采用拉格朗日求梯度进行最小化。