控制系统与仿真CAD（4）——传递函数与状态方程

最新推荐文章于 2024-07-19 21:51:00 发布

比特率

最新推荐文章于 2024-07-19 21:51:00 发布

阅读量571

点赞数 1

分类专栏： Simulink自学记录文章标签： matlab 算法

本文链接：https://blog.csdn.net/qq_36892432/article/details/133441521

版权

Simulink自学记录专栏收录该内容

5 篇文章 1 订阅

订阅专栏

一，传递函数模型

1.线性系统的常系数线性常微分方程模型

$a_1\tfrac{d^{n}y(t)}{dt^n}+a_2\tfrac{d^{n-1}y(t)}{dt^{n-1}}+...+a_n\tfrac{dy(t)}{dt}+a_{n+1}y(t)=b_1\tfrac{d^{m}u(t)}{dt^m}+b_2\tfrac{d^{m-1}u(t)}{dt^{m-1}}+...+b_m\tfrac{du(t)}{dt}+b_{m+1}u(t)$

Laplace变换

传递函数G(s)=Y(s)/U(s)

$G(s)=\tfrac{b_1s^m+b_2s^{m-1}+b_3s^{m-2}+...+b_ms+b_{m+1}}{a_1s^n+a_2s^{n-1}+a_3s^{n-2}+...+a_ns+a_{n+1}}$

MATLAB输入语句

num=[b1,b2,b3,...,bm,bm+1];
den=[a1,a2,a3,...,an,an+1];
G=tf(num,den);

2.传递函数模型

传递函数有2种输入方法。

方法一：分子分母输入法

传递函数G(s)=Y(s)/U(s)

$G(s)=\tfrac{b_1s^m+b_2s^{m-1}+b_3s^{m-2}+...+b_ms+b_{m+1}}{a_1s^n+a_2s^{n-1}+a_3s^{n-2}+...+a_ns+a_{n+1}}$

MATLAB输入语句

num=[b1,b2,b3,...,bm,bm+1];
den=[a1,a2,a3,...,an,an+1];
G=tf(num,den);

Eg:数学模型

$G(s)=\tfrac{12s^3+24s^{2}+12s+20}{2s^4+4s^{3}+6s^{2}+2s+2}$

MATLAB输入语句

num=[12,24,12,20];
den=[2,4,6,2,2];   %%逗号也可以换成空格
G=tf(num,den);

方法二：直接输入法

Eg:数学模型

$G(s)=\tfrac{s^3+2s^{2}+3s+4}{s^3(s+2)[(s+5)^2+5]}$

MATLAB输入语句

s=tf('s');
G=(s^3+2*s^2+3*s+4)/(s^3*(s+2)*((s+5)^2+5);

2.传递函数属性修改

传递函数的属性可以通过get(tf)来查看。

延迟传递函数 $G(s)e^{-3s}$ ，其中 $\tau=3$ ，表示有3秒的延迟。

可以通过对传递函数属性修改，来达到将延迟输入给计算机的目的。

在MATLAB中有3种方式。前两种方式通过语句调用，如下所示：

G.ioDelay=3           %%第一种修改方式
set(G,'ioDelay',3)    %%第二种修改方式

第三种是直接赋值的方法，即在传递函数后面直接乘以exp()：

s=tf('s');
G=(s^3+2*s^2+3*s+4)/(s^3*(s+2)*((s+5)^2+5)*exp(-3*s);

3.多变量系统传递函数矩阵模型

多变量系统不能用单个传递函数表示1，而应该表示为一个传递函数矩阵。

$\begin{bmatrix} g_{11}(s) & g_{12}(s) & ...& g_{1p}(s) \\ g_{21}(s) & g_{22}(s) & ... &g_{2p}(s) \\ ... & ... & ... & ... \\ g_{q1}(s) & g_{q2}(s) & ... & g_{qp}(s) \end{bmatrix}$

其中， $g_{ij}(s)$ 表示第i输出对第j输入的传递函数，可以将 $g_{ij}(s)$ 成为子传递函数。

一般，先定义子传递函数，再通过矩阵定义G(s)。

Eg:多变量传递函数矩阵模型

$G(s)=\begin{bmatrix} \tfrac{0.1134e^{-0.72s}}{1.78s^2+4.48s+1} &\tfrac{0.924}{2.07s+1} \\ \tfrac{0.3378e^{-0.3s}}{0.361s^2+10.9s+1} & \tfrac{-0.318e^{-1.29s}}{2.93s+1} \end{bmatrix}$

方法一：直接输入

MATLAB输入语句

G=[tf(0.1134,[1.78 4.48 1]),tf(0.924,[2.07 1]);tf(0.3378,[0.361 10.9 1]),tf(-0.318,[2.93 1])];    %%中间的分号表示矩阵的换行
G.ioDelay=[0.72 0;0.3,1.29]    %%中间的分号表示矩阵的换行

方法二：先输入子传递函数，再输入传递函数矩阵

先输入各个子传递函数

$\begin{bmatrix} \tfrac{0.1134e^{-0.72s}}{1.78s^2+4.48s+1} &\tfrac{0.924}{2.07s+1} \\ \tfrac{0.3378e^{-0.3s}}{0.361s^2+10.9s+1} & \tfrac{-0.318e^{-1.29s}}{2.93s+1} \end{bmatrix}$

再按照普通矩阵输入的方式输入传递函数矩阵。

MATLAB输入语句

g11=tf(0.1134,[1.78 4.48 1],'ioDelay',0.72);
g12=tf(0.924,[2.07 1]);
g21=tf(0.3378,[0.361 1.09 1],'ioDelay',0.3);
g22=tf(0.1134,[1.78 4.48 1],'ioDelay',0.72);
G=[g111,g12;g21,g22]       %%分号换行

4.传递函数分子分母的提取

对于一般传递函数而言，分子分母的提取直接调用G.num即可。

但是对于传递函数矩阵，无法直接调用G.num。

以上面例子中的2*2传递函数矩阵为例，如果想要调用右下角（第二行第二列）的分子分母，需要调用[num,den]=tfdata(G(2,2),'v')。

二，状态方程

1.状态方程模型

（1）非线性状态方程模型

$\left\{\begin{matrix} \dot{x}_{i}=f_{i}(x_{1},x_{2},...,x_{n},u_{1},...,u_{p}),i=1,...,n \\ y_{i}=g_{i}(x_{1},x_{2},...,x_{n},u_{1},...,u_{p}),i=1,...,q \end{matrix}\right.$

$x_{i}$ 为系统状态变量， $u_{i}$ 为系统输入变量， $y_{i}$ 为系统输出变量。

如果有n个状态变量，这个系统为n阶系统。

上面的 $f_i()$ ， $g_i()$ 为非线性函数，so非线性状态方程。

如果 $f_i()$ ， $g_i()$ 为线性函数，则是线性状态方程。

（2）一般线性状态方程模型

时变

$\left\{\begin{matrix} \dot{x}(t)=A(t)x(t)+B(t)u(t) \\ y(t)=C(t)x(t)+D(t)u(t) \end{matrix}\right.$

时不变

$\left\{\begin{matrix} \dot{x}(t)=Ax(t)+Bu(t) \\ y(t)=Cx(t)+Du(t) \end{matrix}\right.$

MATLAB输入方法：

G=ss(A,B,C,D);

注意：矩阵的维度。

（3）描述符系统（物理可实现VS物理不可实现）

系统模型分为物理可实现和物理不可实现。

物理可实现，即系统的分子阶次不能高于系统的分母阶次。

否则的话，该系统为物理不可实现的系统。

所有物理可实现的系统，都可以表示成上述状态方程的标准形式。

但是物理不可实现的系统如果强行写成上述状态方程的标准形式，会出现状态方程的矩阵不可逆的情况。为此，需要引入描述符系统，将物理不可实现的系统表示为描述符系统的形式。

描述符系统如下所示：

$\left\{\begin{matrix} E\dot{x}(t)=A(t)x(t)+B(t)u(t) \\ y(t)=C(t)x(t)+D(t)u(t) \end{matrix}\right.$

其中，在物理不可实现系统中，E是奇异矩阵。

对于物理可实现的系统，E是单位矩阵。

MATLAB输入方法：

G=ss(A,B,C,D,E);

注意：矩阵的维度。

Eg:状态方程模型

$\dot{x}(t)=\begin{bmatrix} -12 & -17.2 & -16.8 & -11.9\\ 6 & 8.6 & 8.4 & 6\\ 6 & 8.7 & 8.4 & 6\\ -5.9 & -8.6 & -8.3 & -6 \end{bmatrix}x(t)+\begin{bmatrix} 1.5 & 0.2\\ 1 & 0.3\\ 2 & 1\\ 0 & 0.5 \end{bmatrix}u(t)$

$y(t)=\begin{bmatrix} 2 & 0.5 & 0 & 0.8\\ 0.3 & 0.3 & 0.2 & 1 \end{bmatrix}x(t)$

MATLAB代码：

A=[-12,-17.2,-16.8,-11.9;6,8.6,8.4,6;6,8.7,8.4,6;-5.9,-8.6,-8.3,-6];
B=[1.5,0.2;1,0.3;2,1;0,0.5];
C=[2,0.5,0,0.8;0.3,0.3,0.2,1];
D=zeros(2,2);   %%注意矩阵的维度
G=ss(A,B,C,D)

其中，因为D是零矩阵，因此也可以用G=ss(A,B,C,0)代替，即：

MATLAB代码

A=[-12,-17.2,-16.8,-11.9;6,8.6,8.4,6;6,8.7,8.4,6;-5.9,-8.6,-8.3,-6];
B=[1.5,0.2;1,0.3;2,1;0,0.5];
C=[2,0.5,0,0.8;0.3,0.3,0.2,1];
G=ss(A,B,C,0)   %%直接写0，MATLAB可以自动识别矩阵维度

（4）带时间延迟的状态方程

数学模型：

$\left\{\begin{matrix} E\dot{x}(t)=A(t)x(t)+B(t)u(t-\tau_{i}) \\ z(t)=C(t)x(t)+D(t)u(t-\tau_{i}) \\ y(t)=z(t-\tau_{0})\end{matrix}\right.$

从数学模型来看，如果延迟作用在输入信号u(t)上，称为输入延迟，即InputDelay。如果延迟作用在输出信号y(t)上，称为输出延迟，即OutputDelay。

MATLAB代码

G=ss(A,B,C,D,E,'InputDelay',τi,'OutputDelay',τ0)

BUT带时间延迟的模型在实际应用中，光有输入延迟和输出延迟是不够的，SO在MATLAB中还定义了一种带有内部延迟的系统。

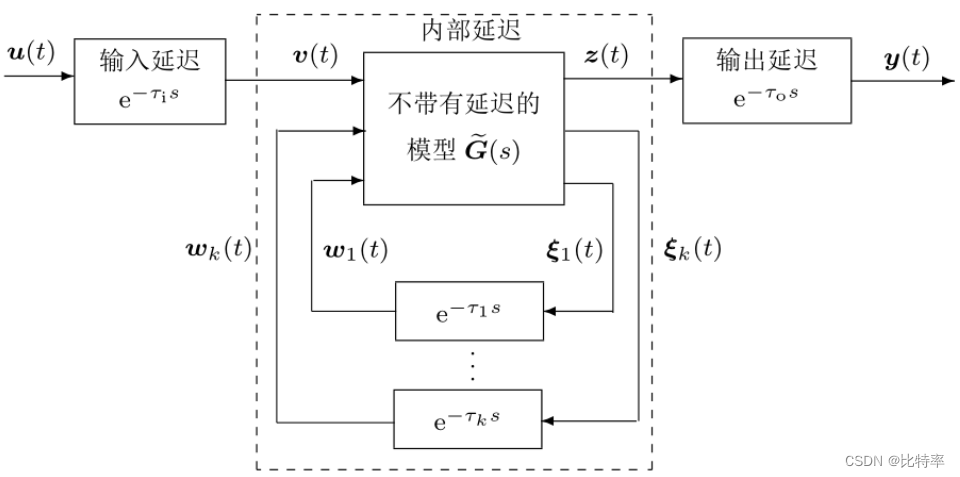
内部延迟是作用在状态信号上的，其中一些状态带有延迟。

2.线性系统的零极点模型

零极点模型：

$G(s)=K\frac{(s-z_1)(s-z_2)...(s-z_m)}{(s-p_1)(s-p_2)...(s-p_n)}$

零点zi，极点pi，增益K

方法一：

z=[z1;z2;...;zm];    %%注意中间用分号
p=[p1;p2;...;pn];
G=zpk(z,p,K)

方法二：

s=zpk('s');
G=...

Eg:零极点模型

$G(s)=\frac{6(s+5)(s+2+j2)(s+2-j2)}{(s+4)(s+3)(s+2)(s+1)}$

方法一：

Z=[-5;-2-2i;-2+2i];    %%中间用分号
P=[-4;-3;-2;-1];
G=zpk(Z,P,6)

方法二：（有些版本可能会出错）

s=zpk('s');
G=6*(s+5)*(s+2+2i)*(s+2-2i)/(s+4)/(s+3)/(s+2)/(s+1)

比特率

关注

1
点赞
踩
4

收藏

觉得还不错? 一键收藏
1
评论
控制系统与仿真CAD（4）——传递函数与状态方程

但是物理不可实现的系统如果强行写成上述状态方程的标准形式，会出现状态方程的矩阵不可逆的情况。为此，需要引入描述符系统，将物理不可实现的系统表示为描述符系统的形式。以上面例子中的2*2传递函数矩阵为例，如果想要调用右下角（第二行第二列）的分子分母，需要调用[num,den]=tfdata(G(2,2),'v')。BUT带时间延迟的模型在实际应用中，光有输入延迟和输出延迟是不够的，SO在MATLAB中还定义了一种带有内部延迟的系统。物理可实现，即系统的分子阶次不能高于系统的分母阶次。
复制链接

扫一扫