回顾,雅可比以及高斯-赛德尔迭代阵。
- 雅可比迭代阵:
- 高斯-赛德尔迭代阵:
迭代法的收敛性
1、充分条件
定理1:若迭代阵 (范数),则迭代法公式
对任意初值均成立。
例:
,判断上述迭代法的收敛性。
由 A 有: ,
,
<1>、对于雅可比迭代法:
(行范数:取 各行数的绝对值之和 最大的那个和值)
雅可比迭代法收敛。
<2>、对于高斯-赛德尔迭代法:
高斯-赛德尔迭代法收敛
求迭代阵很麻烦,下面有一种较方便的方法。
定理2:若 是对角占优方程组,则方程组有唯一解,且雅可比迭代与高斯-赛德尔迭代均收敛。
对角占优阵的定义:设矩阵 满足
,则称
为对角占优阵,称
为对角占优方程组。(即在某一行,对角元素绝对值大于除它以外的所有元素绝对值之和)
例:
显然, 是对角占优阵,雅可比迭代与高斯-赛德尔迭代均收敛。
定理3:设有线性方程组
- 若
对称正定,则高斯-赛德尔迭代收敛;
- 若
对称正定,
也对称正定,则雅可比迭代收敛;
- 若
对称正定,
非正定,则雅可比迭代发散。
矩阵各主子式都大于 0 正定
2、充要条件
谱半径 定义:矩阵 的所有特征值模的最大值,称为
的谱半径,即
.
定理4:迭代公式 对任给初始向量
收敛的充要条件是
。(注意是 迭代阵的谱半径)
例:设 ,
解:显然, 不是对角占优阵,也不对称。
,
都不小于1,所有用定理4.
求 的特征值
令 ,得
故 雅可比迭代收敛。
判断高斯-赛德尔迭代同理,不过 。
总结:对于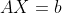 ,判断收敛性
,判断收敛性
为对角占优阵
Jacobbi、Guass-seidel 迭代收敛。
对称正定,则高斯-赛德尔迭代收敛;若
对称正定,
也对称正定,则雅可比迭代收敛。
- 求迭代矩阵
,先判断
,再判断





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








