FIT5216 离散优化问题建模 学习笔记

Week 1

1 MiniZinc 基础建模

1-1 第一个模型

问题：刘备关羽张飞，正招兵买马。他们有10000两银子，并想从冯、刘、赵、简四个村落里面招人。每个村落的壮丁人数和战斗力不一，薪资要求也不一样，刘关张三人想尽可能地利用有限的资金最大化军队的战斗力。

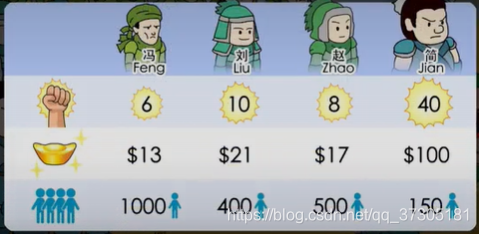
建模：设从冯、刘、赵、简村落招进的人数分别为F、L、Z、J，则有：
13F + 21L + 17Z + 100J <= 10000，
其中 0 <= F <= 1000、0 <= L <= 400、0 <= Z <= 500、0 <= J <= 150，
目标是最大化 6F + 10L + 8Z + 40J；

在MiniZinc中则可以这样表示:

% 定义参数（parameter）
int: budget = 10000;

% 定义约束（constrain）
constraint 13*F + 21*L + 17*Z + 100*J <= budget;

% 定义决策变量（decision variable）
var 0..1000: F;
var 0..400: L;
var 0..500: Z;
var 0..150: J;

% 定义目标（objective）
solve maximize 6*F + 10*L + 8*Z + 40*J;

% 定义输出格式
output ["F = \(F), L = \(L), Z = \(Z), J = \(J)\n"];

知识点
MiniZinc的两种变量
1. Parameters

• 和通常的编程语言一样需要被赋值（only once）
• 数据类型有 int，float，bool，或是这些类型组成的一个范围（set）
• 定义时可以使用 par 关键字，但不是必须的
• 以下定义在逻辑上相等：

  int: i = 3;
  par int: i = 3;
  int: i; i = 3;
  

2. Decision Variables

• 类似于数学上的变量（代数）
• 利用 var 关键字和一个数据类型或和一个范围定义
• 只能被一个表达式赋值一次
• 范围（Range）格式为：a . . b
  – 代表从a至b的所有整数（若a，b为int）
• 以下定义在逻辑上相等：

  var int: i; constraint i >= 0; constraint i <= 4;
  var 0..4: i;
  var {0,1,2,3,4}: i;
  
  var int: i = x + 3;
  var int: i; constraint i = x + 3;
  

MiniZinc的Output and String

• Output格式：output <list of strings>
• String使用“”定义
• \n \t等代表特殊符号
• 内置函数
  – show(v) v值得String形式
  – \(v) 在一串String中显示v的值
  – ++ 用来连接两串Stringe

运行MiniZinc

• 命令行输入 $ minizinc <文件名> 运行文件或利用MiniZinc IDE点击RUN
• 招兵买马问题最后会输出答案：
• 最终战斗力为4752，军队人数为496人
• ------- 代表答案
• ======= 代表最佳答案
• 文件名后缀必须为 .mzn

1-2 第二个模型

问题：刘关张三人在训练士兵的过程中，有士兵逃走，他们三个人现在想知道自己有多少兵，一个个数会消耗很多时间，张飞让全部士兵排成人数相等的5列，剩下两个士兵不能入列，若排成7列，也是剩下两个，排成12列则剩下1个，张飞肯定人数在100至800之间，刘关张现在有多少士兵？

建模：设人数为army，则 100 <= army <= 800，
且 army mod 5 = 2，army mod 7 = 2，army mod 12 = 1;

在MiniZinc中则可以这样表示:

var 100..800: army;

constraint army mod 5 = 2;
constraint army mod 7 = 2;
constraint army mod 12 = 1;

% 由于这个问题不是要找到最优解，而是找到合适的解，因此此处没有objective
solve satisfy;

知识点
默认输出

• 当文件无output语句时, 会默认输出所有被声明且没有被赋值的变量

solve satisfy命令

• 当一个问题不是求最优化值时，用此命令将找出一个适合该模型的解，若想找出所有适合的解，则需配合选项 -all-solutions
• minizinc -all-solutions <文件名>

1-3 第三个模型

问题：刘关张三人想要向张世平购买马匹。张世平出了个问题给他们，若能解决则将马匹卖给他们。张世平拿出一张汉朝地图，给他们四种颜色的颜料，并让他们给图上各个区域填色且相邻的区域不能共享同一种颜色。

MiniZinc建模如下:

enum COLOR = {GREEN, BLUE, PINK, YELLOW};
    
var COLOR: Si;
var COLOR: Yan; 
var COLOR: Yu;
var COLOR: Xu; 
var COLOR: Qing;
var COLOR: Ji; 
var COLOR: You;
var COLOR: Bing; 
var COLOR: Yong;
var COLOR: Liang; 
var COLOR: Yi;
var COLOR: Jing; 
var COLOR: Yang;
var COLOR: Jiao;

constraint Liang != Yong;
constraint Yong != Yi;
constraint Yong != Jing;
constraint Yong != Si;
constraint Yi != Jing;
constraint Yi != Jiao;
constraint Jiao != Jing;
constraint Jiao != Yang;
constraint Jing != Yang;
constraint Jing != Yong;
constraint Jing != Si;
constraint Jing != Yu;
constraint Yang != Yu;
constraint Yang != Xu;
constraint Yu != Si;
constraint Yu != Yan;
constraint Yu != Xu;
constraint Xu != Yan;
constraint Xu != Qing;
constraint Yan != Si;
constraint Yan != Ji;
constraint Yan != Ji;
constraint Yan != Qing;
constraint Qing != Ji;
constraint Ji != You;
constraint Ji != Bing;
constraint Ji != Si;
constraint You != Bing;
constraint Bing != Si;

solve satisfy;

知识点
枚举类型（enumerate type）

• 枚举类型（enums）定义了被命名的objects的有限集合
  – 决策变量或参数可以为枚举类型
  – 数组可以是枚举类型
  – set可以是枚举类型
• 枚举类型声明：enum <enum-name>
• 枚举类型赋值：enum-name = {id1, ..., idn}
• 可以使用枚举类型来声明决策变量：var enum-name: var-name
• 集合中的元素最终将被映射为int后再被计算
• 文件中的参数没有被赋值时，可以利用.dzn文件作文数据文件给参数赋值，命令行输入 minizinc <脚本名> <数据文件名> 即可
• 或者利用-D选项为参数赋值 minizinc armyd.mzn -D"budget = 20000;"

1-4 模型与实例

场景：刘关张需要更多的钱招兵买马，张世平给他们介绍了他的朋友苏双，苏双打算借他们一笔钱，分四个季度还。

• 苏双借给他们的钱为 P （初始balance）
• 每个季度都有固定的regular repayment 为 R
• 每季度的利率为 I
• 在每个季度还款后，刘关张所欠balance为上一次的balance + 上一次balance的利息 - R

模型如下：

% variables
var 0..10000.0: R;        % quarterly repayment
%var float: R;
var float: P;        % principal initially borrowed
var 0.0 .. 2.0: I;  % interest rate

% intermediate variables
var float: B1; % balance after one quarter
var float: B2; % balance after two quarters
var float: B3; % balance after three quarters
var float: B4; % balance owing at end

constraint B1 = P * (1.0 + I) - R;
constraint B2 = B1 * (1.0 + I) - R;
constraint B3 = B2 * (1.0 + I) - R; 
constraint B4 = B3 * (1.0 + I) - R;

solve satisfy;

output [
 "Borrowing ", show_float(0, 2, P), " at ", show_float(0,2,I*100.0), 
 "% interest, and repaying ", show_float(0, 2, R), 
  "\nper quarter for 1 year leaves ", show_float(0, 2, B4), " owing\n"
];

问题1： 如果刘备想借10000，利率为0.04，每季固定还款为2600，四季度后他还剩多少没还？
配合数据文件loan1.dzn:

I = 0.04;
P = 10000.0;
R = 2600.0;

执行命令minizinc loan.mzn loan1.dzn
输出Borrowing 10000.00 at 4.00% interest, and repaying 2600.00 per quarter for 1 year leaves 657.78 owing

问题2：如果刘备想借10000，利率为0.04，他每月须还多少才能在刚好第四季都结束时还清？
数据文件loan2.dzn:

I = 0.04;
P = 10000.0;
B4 = 0.0;

输出Borrowing 10000.00 at 4.00% interest, and repaying 2754.90 per quarter for 1 year leaves 0.00 owing

问题3：如果刘备想借10000，每月还3000，并在第四季度结束时刚好还清，那么利率为多少？
数据文件loan3.dzn:

R = 3000.0;
P = 10000.0;
B4 = 0.0;

输出Borrowing 10000.00 at 7.71% interest, and repaying 3000.00 per quarter for 1 year leaves 0.00 owing

知识点
参数与数据

• 通常数据文件定义参数的值
• 也可以定义枚举类型的值
• eg.
  在color.mzn中：

  enum: COLOR;
  

  在color.dzn中：

  COLOR = {R,W,B,G,P};
  

• 数据文件必须以.dzn结尾
• 数据文件只有赋值语句
  – 通常为参数赋值
  – 也可以为决策变量赋值
• 没在模块中定义的参数必须在数据文件中定义
• 一个模块可以有多份数据文件（类似于类和类的实例）

1-5 Modeling Objects

问题：刘关张为新招来的兵马摆宴席，每样菜色因分量不一而需要不同的大小的盘子，刘关张三人用的桌子（18空间）不同于士兵的桌子（70空间），吃的菜色也与士兵的不同，对于每样菜都有各自的好评度，尽可能利用桌子的空间，最大化一桌菜的好评度


建模如下：

enum DISH;
int: capacity;
array[DISH] of int: satisf;% 数组声明
array[DISH] of int: size;

array[DISH] of var int: amt; % how many of each dish

constraint forall(i in DISH)(amt[i] >= 0);% forall表达式
constraint sum(i in DISH)(size[i] * amt[i]) <= capacity;% sum表达式
solve maximize sum(i in DISH)(satisf[i] * amt[i]);

output ["Amount = ", show(amt), "\n"];

两份数据分别是：

DISH = {SNAKESOUP, GONGBAOFROGS, MAPOTOFU};
capacity = 18;
satisf = [29,19,8];
size = [8,5,3];

DISH = {CHILIFISHHEAD, SAUSAGE, SEACUCUMBER, CHICKEN, FRIEDRICE};
capacity = 70;
satisf = [18,16,14,13,6];
size = [12,10,9,8,4];

知识点
数组

• Range表达式：
  – a . . b 或者
  – enumerate type
• 数组声明：arry[range] of variable declaration
• 数组索引：array-name[index-exp]
• Generator expressions
  – forall(i in range)(bool-expression) 对于在range里面的所有元素，bool-expression须为真
  – sum(i in range)(expression) 对于range里面所有元素，经过expression后累加

1-6 通用模型

问题：招兵买马已经进行的差不多，刘备关羽张飞正计划生产武器——剑、斧、棒、枪、矛；不同的武器攻击力不一样，所需铁（总量5000）、木（总量7500）、锻造时间（总量4000）、木工时间（总量3000）都不一样。在有限的资源中，最大化军队攻击力。

知识点
通用模型

• 这个问题其实和前面某些部分的问题都是相同性质的问题
• Products 都需要 resources
• resources 有限
• 最大化 profit
• 招兵问题
  – resources = 资金
  – products = 士兵
• 宴席问题
  – resources = 桌子空间
  – products = 各种菜色
• 因此可以建立通用模型解决此类问题
</