对于⼀对服从多元正态分布的变量
(
x
,
y
)
,可以写出它们的联合概率密度函数:
根据Bay's rule,
 ,能不能得到条件概率
,能不能得到条件概率
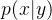 和边缘概率
和边缘概率
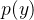 的高斯分布?
的高斯分布?
高斯推断告诉我们是可以的!是左边被拆分成两个部分的形式,因此努力方向是怎么对左边进行差分
根据舒尔补理论:
舒尔补理论Schur Compliment,这简单理解就是一个矩阵分解的方法

两边求逆:

我们只需关注高斯分布的指数部分,代入上式:

这样指数部分就被拆分为两个部分的和,实际可以理解为
与单个变量的多元高斯分布公式形式进行对比

可得他们的高斯形式:

这是一个非常漂亮的结果,我们不仅可以通过联合分布和边缘分布计算条件分布,还说明了有了观测
之后,
的均值做了调整,协方差也减小了,这体现了观测y对状态x的一个修正。

【参考】《机器人学中的状态估计》@深蓝学院










 该博客探讨了一对服从多元正态分布的变量(x, y)的联合概率密度函数,并利用贝叶斯规则解析了条件概率和边缘概率的高斯分布形式。通过舒尔补理论,将指数部分拆分为两部分,展示了如何从联合分布计算条件分布,并指出观测值y对状态x的均值调整和协方差减小,体现了观测的修正作用。
该博客探讨了一对服从多元正态分布的变量(x, y)的联合概率密度函数,并利用贝叶斯规则解析了条件概率和边缘概率的高斯分布形式。通过舒尔补理论,将指数部分拆分为两部分,展示了如何从联合分布计算条件分布,并指出观测值y对状态x的均值调整和协方差减小,体现了观测的修正作用。
















 9665
9665

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








