安全两方推理问题

       分享论文:《Cheetah: Lean and Fast Secure Two-Party Deep Neural Network Inference》

    本文首先介绍该篇论文解决的应用场景:安全两方推理问题。其次介绍如何安全的构造两方推理协议，推理问题可划分为线性计算(如全连接层、卷积层和批标准化层)以及非线性计算(如比较协议(可构造激活函数等)、截断协议等)最后进行论文总结。

安全两方推理问题

两方推理问题指：针对一张图片，有一个模型可以依据图片的属性信息智能的告诉我们这个图片的内容是什么。

假如存在这样的一个场景，Alice拥有一张私有的图片，Bob拥有一个图片识别神经网络模型。现在需要Alice调用Bob的模型来识别自己的私有图片。解决方法有两种，一种是Alice下载模型，但这是属于Bob的私有数据是不被允许的。一种是Alice上传私有图片，但这样Alice的隐私又遭到泄露。因此安全两方推理问题就是为了解决：即不下载模型，也不上传图片，通过运行一个安全的两方计算协议来解决上述问题。

两方推理问题可以将其计算操作划分为线性计算层和非线性计算层。线性层例如全连接层、卷积层和批标准化层等其计算过程主要是矩阵向量乘法。非线性层例如ReLU激活函数,最大池化，最大值参数等其计算操作主要是一个比较过程。另外安全多方计算下很难表示浮点数，因此需要带精度的定点数，定点数就涉及精度溢出问题，需要截断协议。因此主要解决如何高效、精确且安全的实现矩阵向量乘、比较以及截断。

线性计算

线性层主要包括全连接层、卷积层、批标准化层。全连接层的作用是将学到的分布式特征表示映射到样本标记空间。其计算过程实则为将分布式特征向量与权重矩阵相乘加上偏置向量。卷积层的作用是提取图片特征，其计算过程实则为输入张量与卷积核张量内积。批标准化层是一种优化神经网络的方法，其计算过程实则为输入张量与缩放向量的内积。因此在线性计算层主要是解决安全且高效的矩阵向量乘问题。

安全的矩阵向量乘法要求：模型拥有方Alice输入矩阵a,输出随机值r,Bob输入向量b,输出被盲化的矩阵向量积ab-r。除此之外Alice不知晓向量b和ab，Bob不知晓矩阵a和积ab.

我们可以利用同态加密计算实现上述需求：

1.Bob首先生成公私钥对，采用公钥对向量b进行加密，并将加密结果Enc(b)和公钥PK发送给Alice

2.Alice在密文下计算矩阵向量乘得到a*Enc(b)，然后随机生成盲化值r，计算a*Enc(b)-r并发送给Bob

3.Bob因为拥有私钥可解密得到ab-r.

以上步骤即可实现安全的矩阵向量乘的计算。

同态加密方案依据密文支持的算符可分类为半同态加密和全同态加密，而矩阵向量乘法需要支持同态加减法和积运算等，因此需要全同态加密方案。而全同态加密方案中，基于RLWE的全同态方案具有密钥小运行速度快等特点，因此现有的安全两方推理问题多采用基于RLWE的全同态加密。

而基于RLWE的全同态加密方案的明文空间为多项式环，即n-1次多项式中每一个系数都是一个多项式，那么如何将向量编码为多项式是一个问题？

CryptFlow2等先前工作采用名为Packing的方式完成数据编码：首先选择一个分圆多项式，其用于多项式模具有高效的计算性能。明文空间多项式环等于Z(x)mod 分元多项式(  ),可以表示为n个整数。我们首先将数据表示为多项式x，如何模分圆多项式得到在多项式环下的多项式系数为  .从举的例子可知多项式x在多项式环下的多项式系数为4,13.那么给定n个整数如何找到对有的Z(x)来编码呢？可以采用中国剩余定理实现。而且我们发现Packing后在模P上依然保持同态性，因此上述SIMD方式可只进行一次多项式计算即可完成n次的整数运算。

但是我们发现SIMD要求明文模数P必须是素数，那怎么支持非素数的明文域呢？可以采用中国剩余定理实现但这样使得性能会下降若干倍。但是采用该方式的好处是一次乘法即可以完成1000次明文乘法。

现在我们展示如何采用SIMD编码方式来实现向量的内积：

这里举一个例子：

1.Alice和bob分别拥有向量a和b。

2.首先采用SIMD-Pack的方式将向量映射到多项式。

3.然后Bob采用公钥加密多项式B(x)并发送给Alice

4.Alice执行乘法同态得到(  )。但这还远不是内积的结果，还需要做一个加法的聚合。加法的聚合代价较大需要做一个密文旋转的操作。

5.Alice执行n次向左密文旋转，最后对n个密文执行同态加点得到向量内积，然后发送给Bob

6.Bob采用私钥解密得到内积ab。

Cheetah直接采用多项式编码的方式避免了SIMD和旋转操作，提高了计算效率和通信成本。基于  的这样一个事实，观察发现多项式  的常数项正好是a*b。由此粗暴的解决了前面工作遗留的问题。

现在我们就采用上述描述的技术来实现安全的全连接层协议；

1.首先W为Alice拥有的权重矩阵W,向量v由Alice和Bob共有，

2.Alice和Bob分别采用映射函数将向量矩阵映射为多项式。

3.然后Bob加密多项式发送给Alice。

4.Alice在密文下同态计算W*v。Alice不能直接将W*v的系数全部发送给Bob,因为Bob只能获得内积结果不能获得额外的信息。所以Alice要采用同态提取算法提取对应的多项式系数，因此需要将一个加密的多项式转换为一个加密的多项式系数，这也是为什么要用RLWE和LWE两种同态加密。

5.Bob本地解密即可得到向量积。

卷积层和批标准化层采用同意的加密方式故不再赘述。

非线性计算

在2PC-NN非线性计算中，比较和截断一直是影响安全推理效率的一大原因。

因此我们首先介绍如何构造高效的比较协议，其次构造精确且高效的截断协议。

我们通过经典的百万富翁问题说明安全的比较协议定义是什么：有两个百万富翁想要比较下谁更富有，但是又不想透露自己有多少钱。

首先在不考虑安全的情况下执行比较操作的方式：

1.对于长为nbit的数字我们将其表示为2进制形式，然后对其从最高位开始逐一比较，如果相等则进行下一位，否则结束比较。也就是分而治之的方法

这里介绍一个知识，比较中会涉及异或门和与门，目前的研究已经攻破异或门，也就是异或操作已完全免费，仅与门消耗计算开销和通信。所以1-bit的逐一比较是比较耗计算和通信开销的。因此将4-bit划为一块进行比较。

我们如何将其转化为安全的隐私比较协议呢？

1.首先Alice拥有数据x，Bob拥有数据y，数据的二进制长度为l，最小比较单元的二进制长度为m，划分的最小比较单元个数为q=l/m。

2.双方分别划分数据块

3.对于所有的block，Alice和Bob执行  选1不经意传输协议得到比较结果的碎片:

     Alice首先生成两个个随机值r，分别盲化  等于j或小于j的消息然后作为不经意传输的输入消息。

     Bob输入选择bit  ，输出  等于  或小于  的盲化结果。

4.获得所有的block比较结果的共享后，双方按照递推的方式得到x和y的比较结果。

上述的安全比较协议涉及到2选1OT原语,N选1OT原语和海狸三元组原语。

这就涉及到OTE的生成，可以发现基于VOLE的OTE具有极少的通信开销。Cheetah则延续了CryptFlow的比较协议，只是将OTE原语的生成方式进行了替换。

但并不是直接使用Slient OT就能达到最好的效果。如果是在素数域下，基于OT的比较方式是比基于GC的比较方式要慢的。只有在2项域下基于OT的比较方式才能发出效果。(很简单的道理：在二项域下模运算是免费的。)

在MPC框架下，很难表示浮点数，因此都是带精度的的定点数。

这里举个例子：当明文为0.5，精度为  时，做几次乘法后就会出现溢出的情况，因此需要截断。对于秘密共享的密文需要保持截断scale倍或维持scale不变,若直接本地截断会出现致命的错误，例如x=  .

而本地截断的误差来源有两个：一是截断后秘密份额之和溢出时照成的极大误差，二是1/2的概率照成最后1bit的误差。

我们举一个简单的例子来连接这两个误差：首先假设位长为64，截断操作考虑无符号右移，前面位用0填充。秘密份额之和溢出时照成的极大误差指x 和y截断后是否有进位。1/2的概率照成最后1bit的误差：是指x和y截断的部分相加后可能照成最低一位的进位。Cheetah通过实验证明，当时，前者照成极大误差的概率不可忽略，而最后一bit照成的误差不会影响机器学习预测模型的质量。因此可以移除最后一bit误差的约束来构造更简洁的截断协议，从而降低通信和计算开销。

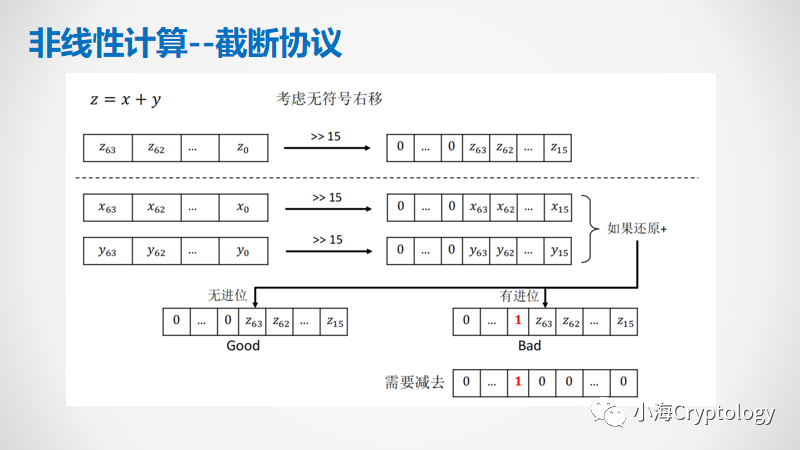
对于上述1-bit修复的安全截断协议描述如下：

1.Alice和Bob分别输入x+y的秘密共享，首先执行一个比较协议，查看x+y是否会有进位。

2.双方采用转换协议将布尔加法秘密共享转换为算术加法秘密共享。

3.Alice和Bob分别本地截断并进行进位修复。

当最高位MSB已知时，

则上述步骤一中只需要Alice和Bob首先执行一个2选1OT即可，如果msb(x)=0,则w=msb(x_a)或msb(x_b),否则w=msb(x_a)与msb(x_b)。

总结

参考文献

[1]Huang Z, Lu W, Hong C, et al. Cheetah: Lean and Fast Secure Two-Party Deep Neural Network Inference[J]. IACR Cryptol. ePrint Arch., 2022, 2022: 207.

[2]Rathee D, Rathee M, Kumar N, et al. CrypTFlow2: Practical 2-party secure inference[C]//Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security. 2020: 325-342.

[3]https://www.bilibili.com/video/BV1B94y1d77U?spm_id_from=333.880.my_history.page.click&vd_source=448cea74ddda4a05b630720ee20091f5

[4]https://zhuanlan.zhihu.com/p/476525705

收录于合集 #多方安全计算(MPC)

 4个

上一篇秘密共享(Secret Sharing,SS)