阅读日期:2020.2.18
二次阅读日期:2020.5.7
github地址: PGPR Method
发现问题
目前,个性化推荐中,基于知识图谱进行推理的方法主要有两大类:
- 利用知识图谱的embedding模型 如TransE、node2vec
主要通过计算实体之间的表示距离来发现它们之间的相似性
缺点:缺乏发现muti-hop关系路径的能力,解释性不够强 - 研究基于路径(path-based)的推荐
缺点:在大规模知识图谱上的执行性不高
针对这两个问题,本文的方法对其做了一定的工作。在下节的前两个解决方法中进行了介绍。(文章思路很清晰,是我目前看的论文中结构最严谨的。当然这篇论文难度也比较大QAQ。。)
面临的挑战及解决方法:
-
问题:如何确定终端条件和强化学习的奖励,从而衡量一个物品是否适合推荐给用户。
解决方法:设计了一个基于多跳评分函数(muti-hop scoring function)的软奖励策略(soft reward strategy),能够在推荐的过程中有效利用知识图谱中丰富的异构信息。 -
问题:如何确定有效的推理路径。由于action space的大小取决于图的出度,一些节点可能非常大。
解决方法:提出一种用户条件动作剪枝策略(user-conditional action pruning strategy),能够对action space进行过滤。 -
问题: 如何保证物品和路径的多样性,以避免在推理的过程中陷入有限区域。
解决方法:设计了一个策略引导的搜索算法(policy-guided search algorithm,即本文提出的PGPR算法),在推理阶段对推荐的推理路径进行有效采样。
相关工作
协同过滤
主要对推荐方法的发展历程进行了简要介绍:从CF出发,后来出现的LFM模型,以及深度学习和神经网络对其的拓展。
这种预测评分的拓展主要分为两类:
①Similarity的学习:采用简单的user/item embeddings(如one-hot向量);学习复杂的预测网络;
②Representation的学习:学习复杂的user/item representations;采用简单的相似度计算函数(如内积)
但二者在可解释推荐上都存在一定的困难。
知识图谱推荐
这部分与发现问题一节的内容类似,故省略。
强化学习
阐述了该研究工作的创新性:首次在知识图谱中运用强化学习的方法来完成推荐任务。
研究方法 —— 重点部分
3.1 问题定义
- k-hop路径
从实体 e 0 e_0 e0到实体 e k e_k ek的k-hop路径,被定义为一个由k +1个实体(entities)通过k个关系(relations)连接的序列

- KGPR-Rec问题
给定:知识图谱 G R G_R GR,用户 u u u,整数 K K K和 N N N
目标:找到 N N N个推荐项目满足 { i n } n ∈ [ N ] ⊆ I \{ i_n \}_{n∈[N]} ⊆ I {in}n∈[N]⊆I
其中,每对 ( u , i n ) (u, i_n) (u,in)与一个推理路径 p k ( u , i n ) ( 2 ≤ k ≤ K ) p_k(u, i_n) (2 ≤ k ≤ K) pk(u,in)(2≤k≤K)相关联
PGPR方法 流程图

其主要思想是训练一个agent,使其能够在知识图谱的环境中,以初始用户为条件,通过强化学习获得能够导航到的潜在的“good item”的能力。然后利用该agent对每个用户的推理路径进行高效的采样,以得到推荐的item。同时,这些采样的路径能够为推荐结果提供解释性。(没太看懂不要紧,看完本章接下来的内容再回顾该流程图会比较易于理解)
3.2 马尔可夫决策过程的建立
将KGPR-Rec问题形式化为马尔可夫决策过程 Markov Decision Process (MDP)
State
t时刻的状态:
s
t
=
(
u
,
e
t
,
h
t
)
s_t=(u, e_t ,h_t )
st=(u,et,ht)
其中,
h
t
h_t
ht是第t步之前的历史。k-step history在Experiment部分对k的选取有做验证
Action
完整的动作空间
A
t
A_t
At:
A
t
=
{
(
r
,
e
)
∣
(
e
t
,
r
,
e
)
∈
G
R
,
e
∉
{
e
0
,
.
.
.
,
e
t
−
1
}
}
At = \{(r, e) | (e_t , r, e) ∈ G_R, e ∉ \{e0, . . . , et−1\}\}
At={(r,e)∣(et,r,e)∈GR,e∈/{e0,...,et−1}}
用户条件剪枝的动作空间
A
~
t
(
u
)
\widetilde{A}_t(u)
A
t(u):
A
~
t
(
u
)
=
{
(
r
,
e
)
∣
r
a
n
k
(
f
(
(
r
,
e
)
∣
u
)
)
≤
α
,
(
r
,
e
)
∈
A
t
}
\widetilde{A}_t(u)=\{(r, e) | rank(f ((r, e) | u)) ≤ α, (r, e) ∈ A_t \}
A
t(u)={(r,e)∣rank(f((r,e)∣u))≤α,(r,e)∈At}
其中α是预定义的action space size上限,而action pruning的评分函数
f
(
(
r
,
e
)
∣
u
)
f ((r, e) | u)
f((r,e)∣u)将在3.3中进行介绍
Reward
只对处于终态给予soft reward,终态奖励
R
T
R_T
RT 定义如下(同时进行了归一化):

其中,另一个关于reward的评分函数
f
(
u
,
i
)
f (u, i)
f(u,i)也在3.3节进行定义
Transition
由于图的属性,state由实体的位置决定。若给定状态
s
t
=
(
u
,
e
t
,
h
t
)
s_t=(u, e_t ,h_t )
st=(u,et,ht)和动作
a
t
=
(
r
t
+
1
,
e
t
+
1
)
a_t=(r_{t+1}, e_{t+1} )
at=(rt+1,et+1),则有到下一状态
s
t
+
1
s_{t+1}
st+1的transition如下:

Optimization
MDP的目标是学习一种随机策略
π
π
π,对于任意初始用户都能够最大化期望累计奖励:

通过强化学习的方法,设计了两个共享相同特征层的策略网络(policy network)和价值网络(value network)
- Policy network π ( ⋅ ∣ s , A ~ u ) π(·|s, \widetilde{A} _u) π(⋅∣s,A u):输入 s s s和 A ~ u \widetilde{A} _u A u,生成每个动作的概率
- Value network
v
^
(
s
)
\widehat{v}(s)
v
(s):将状态
s
s
s映射到一个真实值(作为REINFORCE的baseline)

其中, x x x是关于输入的s所学到的hidden feature,⊙表示Hadamard乘积(对应位置元素的乘积 ( A ∗ B ) i j = a i j ∗ b i j (A * B)_{ij} = a_{ij}*b_{ij} (A∗B)ij=aij∗bij)
策略梯度定义如下:

其中 G G G表示从 s s s到终态 s T s_T sT的折算累积回报
3.3 Muti-hop评分函数
k-hop pattern
r
~
k
=
{
r
1
,
⋅
⋅
⋅
,
r
k
}
\widetilde{r}_k=\{ r_1,···,r_k\}
r
k={r1,⋅⋅⋅,rk}
对于
(
e
0
,
e
k
)
(e_0,e_k)
(e0,ek),若存在
(
e
0
,
⋅
⋅
⋅
,
e
k
−
1
)
(e_0,···,e_{k-1})
(e0,⋅⋅⋅,ek−1)使得如下条件成立,则称
r
~
k
\widetilde{r}_k
r
k是有效的k-hop pattern

1-reverse k-hop pattern
r
~
k
,
j
=
{
r
1
,
⋅
⋅
⋅
,
r
j
,
r
j
+
1
,
⋅
⋅
⋅
,
r
k
}
(
j
∈
[
0
,
k
]
)
\widetilde{r}_{k,j}=\{ r_1,···,r_j,r_{j+1},···,r_k\} (j ∈ [0, k])
r
k,j={r1,⋅⋅⋅,rj,rj+1,⋅⋅⋅,rk}(j∈[0,k])
其中,
(
r
1
,
⋅
⋅
⋅
,
r
j
)
(r_1,···,r_j)
(r1,⋅⋅⋅,rj)为正向,
(
r
j
+
1
,
⋅
⋅
⋅
,
r
k
)
(r_{j+1},···,r_k)
(rj+1,⋅⋅⋅,rk)为反向。当j=0,全部为反向;当j=k,全部为正向。在图中可表示如下关系:
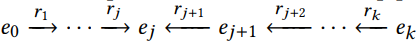
个人理解:通过这种做法,能够获取到知识图谱中更丰富的异构信息(针对图的有向性)
multi-hop 评分函数
该评分函数从数学角度上,可以看做是用于判定两个向量间的相似度

- Action Pruning评分函数
f ( ( r , e ) ∣ u ) = f ( u , e ∣ r ~ k e , j ) f ((r, e) | u) = f (u, e | \widetilde{r}_{k_e,j}) f((r,e)∣u)=f(u,e∣r ke,j)
其中, k e {k_e} ke能使 r ~ k , j \widetilde{r}_{k,j} r k,j成为实体对 ( u , e ) (u, e) (u,e)的valid pattern的最小k值 - Reward 评分函数
f ( u , i ) = f ( u , i ∣ r ~ 1 , 1 ) f (u, i) = f (u, i | \widetilde{r}_{1,1}) f(u,i)=f(u,i∣r 1,1)
简单采用了u和i之间的1-hop pattern作为评分函数,但在实验部分得到2-hop pattern效果更优 - 评分函数的学习
基于以上的定义,我们需要获得entities和relations的embedding来进行评分。那么如何训练得到这些embedding呢?
通过最大化目标函数:

※左半部分:如果 r ~ k , j \widetilde{r}_{k,j} r k,j是valid pattern,则为1;否则为0。
※右半部分:当给定e和 r ~ k , j \widetilde{r}_{k,j} r k,j,得到e’的条件概率 P Ρ P定义如下。当e和e’间的k-hop pattern r ~ k , j \widetilde{r}_{k,j} r k,j,那么就要最大化这个条件概率。

而由于entity set ε ε ε很大,故采用了负采样来近似:

3.4 Policy-Guided Path Reasoning(PGPR)
我们回归到本章的问题定义部分讨论过的,研究的主要目标是解决KGPR-Rec Problem
针对该问题,本研究提出:通过action probability和reward引导的集束搜索(beam search)来探索候选路径和为每个用户的推荐项。
Beam Search(集束搜索)是一种启发式图搜索算法,通常用在图的解空间比较大的情况下,为了减少搜索所占用的空间和时间,在每一步深度扩展的时候,剪掉一些质量比较差的结点,保留下一些质量较高的结点。这样减少了空间消耗,并提高了时间效率,但缺点就是有可能存在潜在的最佳方案被丢弃,因此,Beam Search算法是不完全的,一般用于解空间较大的系统中。
与只选择概率最大的贪心算法相比,集束搜索则选择了概率最大的前k个。这个k值也叫做集束宽度(Beam Width)。
推理算法的伪代码如下:

通过该算法,输出了一组候选T-hop路径
P
T
P_T
PT,以及相应的路径生成概率
Q
T
Q_T
QT和路径奖励
R
T
R_T
RT。通过路径的reward可以对这些路径进行排序,最终将路径对应的item推荐给用户。(如果u和某个i间存在多条路径,通过
Q
T
Q_T
QT选取其中具有最高的生成概率的路径作为推理路径)
实验部分
KGRE-Rec问题的objective:推荐用户在测试集中购买的物品,并为每对user-item提供推理路径
实验环境略。
提到了名词:ablation studies
消融实验( Ablation experiment )可以参考这篇回答——消融实验是什么
4.3 定量分析
通过实验,与baselines的结果进行比较,证明了PGPR方法在4个标准:NDCG, Hit Rate, Recall and Precision上的性能非常良好。实验结果如下:

NDCG:一种衡量排序质量的指标
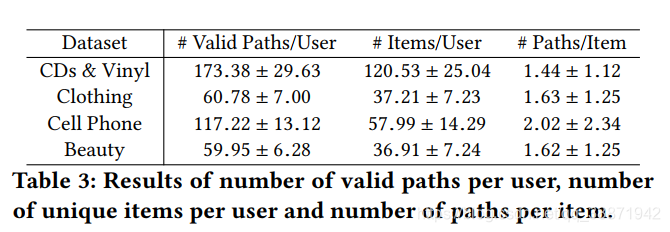
还通过实验验证了PGPR方法发掘的valid path的有效性。其中,每个item约有1.6个推理路径,故可以考虑提供更多的解释性。实验结果如下:
4.4 Action Pruning Strategy的效用
通过实验证明了评分函数能够为初始用户过滤出更具价值的action,证明了该方法是一个良好的指示器。还通过与上一节中表现最好的JRL方法进行了比较,证明了PGPR的有效性。实验结果如下图所示:(蓝色线与红色线,横向四张图的比较)

4.5 Multi-Hop评分函数
实验证明了评分函数的有效性,能够捕获具更长距离的实体间的交互。实验结果如上图所示。(蓝色线与绿色线的比较)
4.6 路径推理中采样大小的选取
通过调整action的采样数量,反映其对路径推理的影响。结果表明前两步的采样大小在寻找"good path"上更重要,可以将其解释为它们在很大程度上决定了最终到达的item是什么类型的。实验结果如下: 
4.7 History Representations
为了验证history representation对方法的影响,通过实验证明了1-step history的效果最好。实验结果如下:

5 案例分析
通过案例,证明了本研究提出方法良好的推荐性能和解释性。


总结与展望
本文主要贡献
- 强调了将丰富的异构信息纳入推荐问题,用以正式定义和解释推理过程的重要性。
- 提出了一种基于强化学习(RL)的方法来解决目前此类方法存在的问题,该方法主要由soft reward策略,user-conditional action pruning和muti-hop评分策略组成。
- 设计了一种基于policy network的定向搜索算法,可以有效地采样各种推理路径和候选项目集合,从而进行推荐。
- 在多个亚马逊电子商务的多个领域(不同数据集)对该方法的有效性进行了评估,获得了良好的推荐结果以及可解释的推理路径。
展望
- 将PGPR用于其他推荐任务,如商品搜索、社交推荐等;
- 将PGPR扩展至time-evolving图中,以提供动态推荐。
























 4804
4804

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








