机械设计介绍--机械传动
1 介绍
1.1 概述
1.2 资料
书籍
机械设计邱宣怀.[第4版]
机械设计 主编 濮良贵 陈国定 吴立言 [第十版] 【西北工业大学】
在线资料
2 机械设计知识整理 【muzing整理编写】
如下由 muzing 编写,本人整理只为了搜索内容方便
详见
主页:https://muzing.top/
整理:https://domm.muzing.top/
******** 第三篇 机械传动 ********
传动的重要性及意义
1.运动形式的改变、运动参数的改变
2.调速
3.一台原动机带多个相互间具有逻辑联系(传动比)的工作机
4.分隔原动机与工作机:保证安全,便于维护
传动的分类

广义的机械传动:
- 摩擦传动
-
- 带传动
-
- 摩擦轮传动
- 啮合传动
-
- 共轭啮合 —— 齿轮传动(直齿斜齿圆柱圆锥、蜗轮蜗杆……)
-
- 非共轭啮合 —— 链传动
- 液压与气动
传动的影响因素
功率
传动比
圆周速度
质量与尺寸
一个典型的传动顺序:带传动 - 齿轮传动 - 链传动
第八章 带传动

8-1 概述
带传动是一种挠性传动
基本组成:
- 主动带轮
- 从动带轮
- 传动带
优点:
- 结构简单
- 传动平稳,噪声小
- 价格低廉
- 缓冲吸振,有过载保护特性
- 安装精度要求低
- (与齿轮比)中心距可以较大
缺点:
- 有弹性滑动、打滑现象,导致传动效率低、传动比不准确
- 尺寸轮廓大
- 压轴力大
- 带的寿命短
带传动的类型
-
摩擦型
-
- 平带
结构简单、传动效率高、带轮易制造
传动中心距较大情况下应用较多
- 平带
-
- 圆带
结构简单
多用于小功率传动
- 圆带
-
- V带
截面呈等腰梯形
允许的传动比大、结构紧凑
大多数V带已标准化
- V带
-
- 多楔带
兼具平带柔性好和V带摩擦力大的优点
解决多根V带长短不一而使各带受力不均的问题
主要用于传递功率较大同时要求结构紧凑的场合
- 多楔带
-
- 啮合型(同步带传动)
保证严格传动比
对中心距及其尺寸稳定性要求较高
- 啮合型(同步带传动)
V带传动




按带轮轴线位置关系:
- 平行轴
- 交错轴
- 半交叉传动
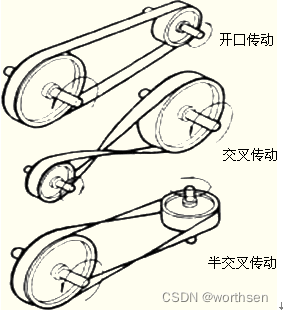
V带的类型与结构
V带形式按结构分:
- 包边V带
- 切边V带

带由 胶帆布 1 、顶胶 2 、芯绳 3 和底胶 4 等部分组成
带型:
- 普通V带具有对称的梯形横截面
- 带型分为 Y、Z、A、B、C、D、E 7种,按顺序依次增大
- 楔角均为 40°
- 截面尺寸:查表
窄V带:
- 相同带宽度,窄V带的高度约比普通V带增加 1/3
- 比相同带宽度的普通V带承载能力有较大提高
- 适用于传递功率较大同时又要求外形尺寸较小的场合
- 带型分为 SPZ、SPA、SPB、SPC 4种
节宽
b
p
b_p
bp :
V带垂直于其顶面弯曲(包裹到带轮上)时,从截面看,顶胶(受拉)变窄,底胶(受压)变宽。顶胶和底胶之间的某个位置处宽度保持不变,该宽度即为节宽
b
p
b_p
bp
基准长度
L
d
L_d
Ld:
把V带套在规定尺寸的测量带轮上,在规定的张紧力下,沿V带的节宽巡行一周,即为V带的基准长度
L
d
L_d
Ld
其他V带:
联组V带、齿形V带、大楔角V带、宽V带等

8-2 带传动工作情况的分析
带传动的受力分析
初拉力
F
0
F_0
F0
带传动工作前,传动带以一定的初拉力
F
0
F_0
F0 张紧在带轮上
紧边拉力
F
1
:
F
1
=
F
0
+
F
e
/
2
F_1: F_1 = F_0 + F_e / 2
F1:F1=F0+Fe/2
松边拉力
F
2
:
F
2
=
F
0
−
F
e
/
2
F_2: F_2 = F_0 - F_e / 2
F2:F2=F0−Fe/2
近似认为带的总长度保持不变,并假设带为弹性线体,则紧边拉力的增加量等于松边拉力的减少量
有效拉力 F e F_e Fe: F e = F f = F 1 − F 2 F_e = F_f = F_1 - F_2 Fe=Ff=F1−F2
| 字母符号 | 含义 |
|---|---|
| F e F_e Fe | 带传动的有效拉力 |
| F f F_f Ff | 带传动工作表面上的总摩擦力 |
| F 1 F_1 F1 | 紧边拉力 |
| F 2 F_2 F2 | 松边拉力 |
有效拉力
F
e
F_e
Fe 与带传动所传递的功率 P 的关系为:
P
=
F
e
v
1000
P = \frac{F_e v}{1000}
P=1000Fev
| 字母符号 | 物理量 | 单位 |
|---|---|---|
| P | 功率 | kW |
| F e F_e Fe | 有效拉力 | N |
| v v v | 传送带速度 | m/s |
当其他条件不变且初拉力 F 0 F_0 F0 一定时,摩擦力 F f F_f Ff 有一极限值(临界值),这个极限值限制着带传动的传动能力
离心拉力
F
c
F_c
Fc
F
c
=
q
v
2
F_c = q v^2
Fc=qv2
| 字母符号 | 含义 |
|---|---|
| F c F_c Fc | 离心拉力 |
| q | 带的线密度 |
| v | 带速 |
带传动的最大有效拉力 F e c F_{ec} Fec 及其影响因素
由柔韧体摩擦的欧拉公式可知紧边拉力
F
1
F_1
F1 和松边拉力
F
2
F_2
F2 在摩擦力最大值时的关系:
F
1
=
F
2
e
f
v
α
F_1 = F_2 e^{f v \alpha}
F1=F2efvα
| 字母符号 | 含义 |
|---|---|
| F 1 F_1 F1 | 紧边拉力 |
| F 2 F_2 F2 | 松边拉力 |
| e e e | 自然对数的底数,e = 2.718⋯ |
| f v f_v fv | 当量摩擦因数 |
| α \alpha α | 带在带轮上的包角,rad |
小带轮包角 α 1 \alpha_1 α1 、大带轮包角 α 2 \alpha_2 α2 :
α
1
≈
180
°
−
(
d
d
2
−
d
d
1
)
57.3
°
a
\alpha_1 \approx 180° - (d_{d2} - d_{d1})\frac{57.3°}{a}
α1≈180°−(dd2−dd1)a57.3°
α
2
≈
180
°
+
(
d
d
2
−
d
d
1
)
57.3
°
a
\alpha_2 \approx 180° + (d_{d2} - d_{d1})\frac{57.3°}{a}
α2≈180°+(dd2−dd1)a57.3°
| 字母符号 | 含义 |
|---|---|
| α 1 , α 2 \alpha_1, \alpha_2 α1,α2 | 小带轮包角、大带轮包角,° |
| d d 1 , d d 2 d_{d1}, d_{d2} dd1,dd2 | 小带轮、大带轮基准直径,mm |
| a a a | 带轮中心距,mm |
对V带轮来说,基准直径就是带轮槽宽尺寸等于带的节宽 b p b_p bp 处的直径
最大有效拉力
F
e
c
,
F
1
F
2
F_{ec}, F_1 F_2
Fec,F1F2 临界值:
F
e
c
=
2
F
0
e
f
v
α
−
1
e
f
v
α
+
1
F_{ec} = 2F_0 \frac{e^{f v \alpha} - 1}{e^{f v \alpha} + 1}
Fec=2F0efvα+1efvα−1
式中的包角 α \alpha α 应取 α 1 \alpha_1 α1 和 α 2 \alpha_2 α2 中的较小者
影响最大有效拉力 F e c F_{ec} Fec 的因素:
- 初拉力 F 0 F_0 F0
-
- F e c F_{ec} Fec 与 F 0 F_0 F0 成正比
-
- F 0 F_0 F0 过大时,将使带的磨损加剧,以致过快松弛,缩短带的工作寿命
-
- F 0 F_0 F0 过小时,带的工作能力得不到充分发挥,运转时容易发生跳动和打滑
- 包角 α \alpha α
-
- F e c F_ec Fec 随包角 a l p h a alpha alpha 的增大而增大
- (当量)摩擦因数
f
v
f_v
fv
* * F e c F_ec Fec 随摩擦因数 f f f 的增大而增大 -
- f v f_v fv 与带及带轮的材料和表面状况、工作环境有关
带的应力分析
拉应力
σ 1 = F 1 A \sigma_1 = \frac{F_1}{A} σ1=AF1
σ 2 = F 2 A \sigma_2 = \frac{F_2}{A} σ2=AF2
| 字母符号 | 含义 | 单位 |
|---|---|---|
| σ 1 \sigma_1 σ1 | 紧边拉应力 | MPa |
| σ 2 \sigma_2 σ2 | 松边拉应力 | MPa |
| A | 传动带的横截面积 | mm² |
弯曲应力
σ
b
1
≈
E
h
d
d
1
\sigma_{b1} \approx E \frac{h}{d_{d1}}
σb1≈Edd1h
σ
b
2
≈
E
h
d
d
2
\sigma_{b2} \approx E \frac{h}{d_{d2}}
σb2≈Edd2h
| 字母符号 | 含义 | 单位 |
|---|---|---|
| h | 传送带的高度 | mm |
| E | 传送带的弹性模量 | MPa |
带的弯曲应力与带轮的基准直径成反比,因此带在小带轮上的弯曲应力 σ b 1 \sigma_{b1} σb1 大于在大带轮上的弯曲应力 σ b 2 \sigma_{b2} σb2。
离心拉应力
当带随着带轮作圆周运动时,由于带自身的质量会引起离心力,进而在带中产生离心拉力。这个力存在于带的全长范围内。
σ c = q v 2 A \sigma_c = \frac{qv^2}{A} σc=Aqv2
| 字母符号 | 含义 | 单位 |
|---|---|---|
| q | 传送带单位长度的质量 | kg/m |
| v | 带的线速度 | m/s |

带中可能产生的瞬时最大应力发生在带的紧边开始绕上小带轮处,最大拉应力可以近似表示为:
σ max ≈ σ 1 + σ b 1 + σ c \sigma_{\max} \approx \sigma_1 + \sigma_{b1} + \sigma_c σmax≈σ1+σb1+σc
带在运动过程中,带上任意一点的应力都发生变化。
带每巡行一周,相当于应力变化的一个周期。当带工作一定的时间之后,可能会因为疲劳而发生断裂或者塑性变形。
带的弹性滑动和打滑
弹性滑动
传送带在受到拉力作用时会发生弹性变形。在小带轮上,带的拉力从紧边拉力
F
1
F_1
F1 逐渐降低到松边拉力
F
2
F_2
F2,带的弹性变形量逐渐减小,因此带相对于小带轮向后退缩,使得带的速度低于小带轮的线速度
v
1
v_1
v1;类似的,在大带轮上带的速度高于大带轮的线速度
v
2
v_2
v2。带的拉应力变化导致带长变化,进而导致带与带轮间产生相对滑动,即为弹性滑动。
由于带的弹性变形而引起的带与带轮间的微量滑动,总是存在无法避免。
-
滑动率 ε \varepsilon ε:
一个循环中,带速不变,但大带轮的线速度 v 2 v_2 v2 小于小带轮线速度 v 1 v_1 v1。带轮线速度的相对变化量可以用滑动率 ε \varepsilon ε 衡量。评价带轮线速度的相对变化量为:ε = v 1 − v 2 v 1 × 100 % \varepsilon = \frac{v_1 - v_2}{v_1} \times 100\% ε=v1v1−v2×100%
带传动的平均传动比
i = n 1 n 2 = d d 2 ( 1 − ε ) d d 1 i = \frac{n_1}{n_2} = \frac{d_{d2}}{(1-\varepsilon)d_{d1}} i=n2n1=(1−ε)dd1dd2
在一般的带传动中,因滑动率不大( ε \varepsilon ε ≈ 1% ~2%),可忽略,而取传动比为:
i ≈ n 1 n 2 ≈ d d 2 d d 1 i \approx \frac{n_1}{n_2} \approx \frac{d_{d2}}{d_{d1}} i≈n2n1≈dd1dd2

滑动弧与静止弧
- 带的弹性滑动只发生在带离开主、从动带轮之前的那一段接触弧上,称为滑动弧(图中 C 1 B 1 ^ \widehat{C_1B_1} C1B1 和 C 2 B 2 ^ \widehat{C_2B_2} C2B2 ),所对中心角为滑动角。
- 没有发生弹性滑动的接触弧,称为静止弧(图中 A 1 C 1 ^ \widehat{A_1C_1} A1C1 和 A 2 C 2 ^ \widehat{A_2C_2} A2C2 ),所对中心角为静止角。
整体打滑
- 带传动功率超过极限,带与带轮之间发生显著的相对滑动。
- 滑动弧增大,扩大至整个接触弧时,发生整体打滑。
- 加剧带的磨损、降低从动轮转速、甚至使传动失效,应极力避免。
- 当带传动所传递的功率突然增大而超过设计功率时,这种打滑却可以起到过载保护的作用。
8-3 普通V带传动的设计计算
设计准则和单根V带的基本额定功率 P 0 P_0 P0
带传动的设计准则:在保证带传动不打滑的条件下,使带具有所需的疲劳强度和寿命。
V带 疲劳强度条件:
σ
max
≈
σ
1
+
σ
b
1
+
σ
c
≤
[
σ
]
\sigma_{\max} \approx \sigma_1 + \sigma_{b1} + \sigma_c \leq [\sigma]
σmax≈σ1+σb1+σc≤[σ]
或
σ
1
≤
[
σ
]
−
σ
b
1
−
σ
c
\sigma_1 \leq [\sigma] - \sigma_{b1} - \sigma_c
σ1≤[σ]−σb1−σc
式中, [ σ ] [\sigma] [σ] 为在一定条件下,由带的疲劳强度所决定的许用应力。
最大有效拉力 F e c F_{ec} Fec:
F e c = F 1 ( 1 − 1 e f v α ) = σ 1 A ( 1 − 1 e f v α ) F_{ec} = F_1 \left(1 - \frac{1}{e^{f_v \alpha}}\right) = \sigma_1 A \left(1 - \frac{1}{e^{f_v \alpha}}\right) Fec=F1(1−efvα1)=σ1A(1−efvα1)
基本额定功率 P 0 P_0 P0:
P 0 = ( [ σ ] − σ b 1 − σ c ) ( 1 − 1 e f v α ) A v 1000 P_0 = \frac{([\sigma] - \sigma_{b1} - \sigma_c)(1 - \frac{1}{e^{f_v \alpha}})Av}{1000} P0=1000([σ]−σb1−σc)(1−efvα1)Av
| 字母符号 | 含义 |
|---|---|
| P 0 P_0 P0 | 单根V带所允许传递的功率,kW |
| [ σ \sigma σ] | 许用应力 |
| σ b 1 \sigma_{b1} σb1 | 小带轮上的弯曲应力 |
| σ c \sigma_c σc | 离心拉应力 |
| f v f_v fv | 当量摩擦因数 |
| α \alpha α | 包角 |
单根普通V带的基本额定功率 P 0 P_0 P0 通过 试验 得到,具体数值:查表。
单根V带的额定功率 P r P_r Pr
实际工作情况条件与试验条件不同,需要对单根V带的基本额定功率予以修正,得到单根V带的 额定功率
P
r
P_r
Pr:
P
r
=
(
P
0
+
Δ
P
0
)
K
α
K
L
P_r = (P_0 + \Delta P_0) K_{\alpha} K_L
Pr=(P0+ΔP0)KαKL
| 字母符号 | 含义 |
|---|---|
| Δ P 0 \Delta P_0 ΔP0 | 当传动比不等于1时,单根V带额定功率的增量,查表 |
| K α K_{\alpha} Kα | 当包角小于180°时的修正系数,查表 |
| K L K_L KL | 当带长不等于试验规定的特定带长时的修正系数,查表 |
带传动的参数选择
中心距 a a a
中心距 大 的优点:
- 增加带轮的包角
- 减小单位时间内带的循环次数
- 有利于提高带的寿命
中心距 过大 的缺点:
- 加剧带的波动
- 降低带传动的平稳性
- 增大带传动的整体尺寸
初选带传动中心距:
0.7
(
d
d
1
+
d
d
2
)
≤
a
0
≤
2
(
d
d
2
+
d
d
2
)
0.7(d_{d1} + d_{d2}) \leq a_0 \leq 2(d_{d2} + d_{d2})
0.7(dd1+dd2)≤a0≤2(dd2+dd2)
a 0 a_0 a0 为初选的带传动中心距,mm
传动比 i i i
传动比大,则小带轮的包角将减小,带传动的承载能力降低,故带传动的传动比不宜过大:
- i ≤ 7 i \leq 7 i≤7 (一般)
- 2 ≤ i ≤ 5 2 \leq i \leq 5 2≤i≤5 (推荐)
带轮的基准直径 d d d_d dd
小带轮直径太 小 的缺点:
- 带速减小,单根V带所能传递的功率减小,增加V带根数,增大带轮宽度,且增大载荷在V带之间分配的不均匀性
- 带的弯曲应力增大
小带轮的基准直径不宜太小,一般应保证 d d ≥ ( d d ) min d_d \geq (d_d)_{\min} dd≥(dd)min (查表)
带速 v v v
带速 高 的优点:
- 单根V带所能传递的功率增大
- 相应可以减小带的根数,或减小V带的横截面积,使带传动的总体尺寸减小
带速 过高 的缺点:
- 带中的离心应力增大,使得单根V带所能传递的功率降低
- 带的寿命降低
带速 过低 的缺点:
- 单根V带所能传递的功率过小,带的根数增多
- 带传动的能力没有得到发挥
带速推荐值:
- v = 5 ∼ 25 v = 5 \sim 25 v=5∼25 m/s (推荐)
- v max < 30 v_{\max} < 30 vmax<30 m/s
从充分发挥带的工作能力和减小带传动的总体尺寸考虑,在多级传动中应将带传动设置在高速级。
带传动的设计计算
已知条件包括带传动的工作条件、传动位置与总体尺寸限制、所需传递的额定功率 P P P、小带轮转速 n 1 n_1 n1、大带轮转速 n 2 n_2 n2 或传动比 i i i。
设计内容涵盖选择带的型号、确定基准长度、根数、中心距、带轮的材料、基准直径以及结构尺寸、初拉力和压轴力、张紧装置等。
(1)确定计算功率
P
c
a
=
K
A
P
P_{ca} = K_A P
Pca=KAP
| 字母符号 | 含义 |
|---|---|
| P c a P_{ca} Pca | 计算功率,kW |
| K A K_A KA | 工作情况系数,查表 |
| P P P | 所需传递的额定功率,kW |
(2)选择V带的类型
根据计算功率
P
c
a
P_{ca}
Pca 和小带轮转速
n
1
n_1
n1,查表选取普通V带的带型。
(3)确定带轮的基准直径
d
d
d_d
dd 并验算带速
v
v
v
初选小带轮的基准直径
d
d
1
d_{d1}
dd1,应使
d
d
1
≥
(
d
d
)
min
d_{d1} \geq (d_d)_{\min}
dd1≥(dd)min。
验算带速 v v v,一般 v = 5 ∼ 25 v = 5 \sim 25 v=5∼25 m/s, v max < 30 v_{\max} < 30 vmax<30 m/s。
计算大带轮的基准直径,由 d d 2 = i d d 1 d_{d2} = i d_{d1} dd2=idd1 计算,并根据表适当圆整。
(4)确定中心距
a
a
a 并选择V带的基准长度
L
d
L_d
Ld
根据带传动总体尺寸的限制条件或要求的中心距,结合带初选中心距公式,计算初定中心距
a
0
a_0
a0。
计算相应的带长 L d 0 L_{d0} Ld0:
L d 0 ≈ 2 a 0 + π 2 ( d d 1 + d d 2 ) + ( d d 2 − d d 1 ) 2 4 a 0 L_{d0} \approx 2a_0 + \frac{\pi}{2}(d_{d1}+d_{d2}) + \frac{(d_{d2} - d_{d1})^2}{4a_0} Ld0≈2a0+2π(dd1+dd2)+4a0(dd2−dd1)2
带的基准长度 L d L_d Ld 根据 L d 0 L_{d0} Ld0 由查表选取。
计算中心距 a a a 及其变动范围:
传动的实际中心距近似为
a ≈ a 0 + L d − L d 0 2 a \approx a_0 + \frac{L_d - L_{d0}}{2} a≈a0+2Ld−Ld0
中心距变动范围
a
min
=
a
−
0.015
L
d
a_{\min} = a - 0.015L_d
amin=a−0.015Ld
a
max
=
a
+
0.03
L
d
a_{\max} = a + 0.03L_d
amax=a+0.03Ld
(5)验算小带轮上的包角 α 1 \alpha_1 α1
α 1 ≈ 18 0 ∘ − ( d d 2 − d d 1 a ) × 57. 3 ∘ ≥ 12 0 ∘ \alpha_1 \approx 180^{\circ} - \left(\frac{d_{d2} - d_{d1}}{a}\right) \times 57.3^{\circ} \geq 120^{\circ} α1≈180∘−(add2−dd1)×57.3∘≥120∘
(6)确定带的根数 z z z
z = P c a P r = K A P ( P 0 + Δ P 0 ) K α K L z = \frac{P_{ca}}{P_r} = \frac{K_AP}{(P_0 + \Delta P_0)K_{\alpha} K_L} z=PrPca=(P0+ΔP0)KαKLKAP
为了使各根V带受力均匀,带的根数不宜过多,一般应少于10根。否则应选择横截面积较大的带型,以减少带的根数。
(7)确定带的初拉力
F
0
F_0
F0
单根V带初拉力可由下式确定:
F 0 = 500 ( 2.5 − K α ) P c a K α z v + q v 2 F_0 = 500 \frac{(2.5-K_{\alpha})P_{ca}}{K_{\alpha} zv} + qv^2 F0=500Kαzv(2.5−Kα)Pca+qv2
控制实际
F
0
F_0
F0 大小
安装V带时采用图示方法控制实际初拉力大小,在V带与两带轮切点的跨度中点
M
M
M 施加一规定的、与带边垂直的力
G
G
G,使得带在每 100 mm 上产生的挠度
y
y
y 为1.6 mm(挠度角为 1.8°)。
G值计算方法
| 情况 | 计算公式 |
|---|---|
| 新安装的V带 | G = 1.5 F 0 + Δ F 0 16 G = \frac{1.5F_0 + \Delta F_0}{16} G=161.5F0+ΔF0 |
| 运转后的V带 | G = 1.3 F 0 + Δ F 0 16 G = \frac{1.3F_0 + \Delta F_0}{16} G=161.3F0+ΔF0 |
| 最小极限值 | G = F 0 + Δ F 0 16 G = \frac{F_0 + \Delta F_0}{16} G=16F0+ΔF0 |
| 字母符号 | 含义 |
|---|---|
| G | 垂直力,N |
| F 0 F_0 F0 | 单根V带初拉力 |
| Δ F 0 \Delta F_0 ΔF0 | 初拉力的增量,N,查表 |
(8)计算带传动的压轴力
F
p
F_p
Fp
为了设计安装带轮的轴和轴承,需要计算带传动作用在轴上的压轴力
F
p
F_p
Fp,不考虑带两边的压力差,则压轴力可以近似地按带两边的初拉力的合力计算:
F p = 2 z F 0 sin α 1 2 F_p = 2zF_0 \sin \frac{\alpha_1}{2} Fp=2zF0sin2α1
式中 α 1 \alpha_1 α1 为小带轮的包角。
8-4 V带轮的设计
V带轮的设计内容
根据带轮的基准直径和带轮转速等已知条件,确定带轮的材料,结构形式,轮槽、轮辐和轮毂的几何尺寸,公差和表面粗糙度以及相关技术要求。
带轮材料
常用材料:HT150 或 HT200(灰铸铁);转速较高:铸钢、钢板冲压后焊接而成;小功率:铸铝、塑料。
带轮的结构形式
带轮基准直径 d d d_d dd 的不同尺寸对应的结构形式如下表:
| 尺寸 | 结构形式 |
|---|---|
| d d ≤ 2.5 d d_d \leq 2.5d dd≤2.5d (d 为安装带轮轴的直径) | 实心式 |
| d d ≤ 300 d_d \leq 300 dd≤300 mm | 腹板式 |
| $d_d \leq 300 $ mm 且 D 1 − d 1 ≥ 100 D_1 - d_1 \geq 100 D1−d1≥100 mm | 孔板式 |
| d d > 300 d_d > 300 dd>300 mm | 轮辐式 |
轮毂和轮辐尺寸:查表见经验公式。
V带轮的轮槽
轮槽与所选用的V带型号相对应,查表。V带轮槽的工作面夹角小于40°(32° 34° 36° 38°),以使V带的工作面与带轮的轮槽工作面紧密贴合。轮槽工作表面的表面粗糙度为 R a = 1.6 R_a = 1.6 Ra=1.6 µm 或 R a = 3.2 R_a = 3.2 Ra=3.2 µm。
V带轮的技术要求
- 表面缺陷修补。
- 转速低于极限转速的带轮要做静平衡,高于极限转速的要做动平衡。
- 符合标准GB/T 13575.1-2008。
8-5 V带传动的张紧、安装与防护
V带传动的张紧
定期张紧装置:采用定期改变中心距的方式来调节带的初拉力,使带重新张紧
滑道式带传动定期张紧装置动画

摆架式带传动定期张紧装置动画

自动张紧装置:利用自重、弹簧等实现
带传动自动张紧装置动画
采用张紧轮的张紧装置
带传动张紧轮装置动画
张紧轮:
- 一般应放在松边的内侧,使带只受单向弯曲
- 尽量靠近大链轮,以免减小带在小带轮上的包角
- 轮槽尺寸与带轮的相同
- 直径小于小带轮的直径
- 中心距过小时,可将张紧轮设置在带的松边外侧,同时靠近小带轮(缺点是使带产生反向弯曲,降低带的疲劳寿命)
V带传动的安装
- 各带轮轴线相互平行
- 各带轮相对应的V形槽的对称平面应重合,误差不得超过 20′
- 多根V带传动时,带的配组公差应该规定范围内,以避免各根V带载荷分布不均
V带传动的防护
安全起见,带传动应置于铁丝网或保护罩之内,使之不能外露
第九章 链传动

KAWASAKI-H2R-2015,引擎输出轴与驱动轮间使用单排链传动
9-1 链传动的特点及应用
链传动是一种挠性传动,通过链轮轮齿与链条链节的啮合来传递运动和动力。
组成:
- 链条
- 小链轮
- 大链轮
链传动优点:
- (与摩擦型带传动比)
- 保持准确的平均传动比
- 传动效率高
- 作用于轴上的径向压力小
- 链传动的整体尺寸较小,结构较为紧凑
- 能在高温的潮湿环境中工作
- (与齿轮传动比)
- 制造安装精度要求较低
- 成本较低
- 在远距离传动时,比齿轮传动轻便得多
链传动缺点:
- 只能实现平行轴间链轮的同向传动
- 运转时不能保持恒定的瞬时传动比
- 磨损后易发生跳齿
- 工作时有噪声
- 不宜用在载荷变化很大、高速、急速反向的传动中
应用场合:
- 要求工作可靠
- 两轴相距较远
- 低速重载
- 工作环境恶劣
- 其他不宜使用齿轮传动的场合
链条按用途分类:
- 传动链
-
- 短节距精密滚子链(简称滚子链)
-
- 齿形链
- 输送链
- 起重链
9-2 传动链的结构特点
滚子链
- 一般传递的功率在 100 kW 以下
- 链速不超过 15 m/s
- 推荐使用的最大传动比 i m a x = 6 i_{max} = 6 imax=6
滚子链结构:
- 滚子
- 套筒
- 销轴
- 内链板
- 外链板

配合方式:
- 过盈配合
-
- 内链板与套筒之间
-
- 外链板与销轴之间
- 间隙配合
-
- 滚子与套筒之间
-
- 套筒与销轴之间
活动方式:
- 内、外链板相对挠曲时,套筒可绕销轴自由转动
- 滚子活套在套筒上,工作时沿链轮齿廓滚动,以减轻齿廓的磨损
- 销轴与套筒接触面是链的主要磨损位置,应在内、外链板间留少许间隙,便于润滑油渗入
链板制成 8 字形:
- 使各个横截面具有接近相等的抗拉强度
- 减小链的质量和运动时的惯性力
多排链:
传递大功率时可以使用多排链,排数越多承载能力越强
但受限于精度,各排链承受的载荷不易均匀,故排数不宜过多

接头形式:


滚子链和链轮啮合的基本参数:
- 节距 p (主要参数)
- 滚子外径 d 1 d_1 d1
- 内链节内宽 b 1 b_1 b1
- 排距 p t p_t pt (多排链)

我国链条标准:
GB/T 1243-2006 传动用短节距精密滚子链、套筒链、附件和链轮
链号数 × 25.4 16 \frac{25.4}{16} 1625.4 = 节距值
后缀 A 或 B 表示 A 系列(适用于以美国为中心的西半球区域,主要)或 B 系列(欧洲区域)
滚子链的标记:
链号 - 排数 - 整链链节数 标准编号
例:08A-1-88 GB/T 1243-2006 表示 A 系列、节距 12.7 mm、单排、88 节的滚子链
齿形链
又称无声链,由一组带有两个齿的链板左右交错并铰接而成

齿楔角:
- 每个链板的两个外侧直边(工作边)间的夹角
- 一般为 60°

内导板齿形链导向性好,工作可靠,适用于高速重载传动
链轮宽度大于25 ~ 30 mm 时,一般采用内导板齿形链

外导板齿形链结构简单但导向性差,链轮宽度较小时使用
齿形链优点:
- 传动平稳、噪声小
- 承受冲击性能好
- 效率高
- 工作可靠
应用场合:高速、大传动比、小中心距等工作条件较为严酷的场合
齿形链缺点:结构复杂、难于制造、价格较高
9-3 滚子链链轮的结构和材料
链轮由轮齿、轮缘、轮辐和轮毂组成。链轮设计主要是确定其结构和尺寸,选择材料和热处理方法。
链轮齿形
非共轭啮合
端面:实际齿槽形状取决于加工轮齿的刀具和加工方法,并应使其位于最小和最大齿槽形状之间,常用“三圆弧一直线”

轴面:应作图
查表:滚子链链轮的齿槽形状
链轮的基本参数和主要尺寸
基本参数:
- 配用链条的节距 p
- 滚子外径 d 1 d_1 d1
- 排距 p t p_t pt
- 齿数 z z z
链轮的主要尺寸和计算公式:查表

链轮的结构
| 尺寸 | 结构 |
|---|---|
| 小直径 | 整体式 |
| 中等直径 | 孔板式 |
| 大直径 | 可将齿圈用螺栓连接或焊接在轮毂上 |
链轮的材料
小链轮应采用较好的材料制造
链轮常用材料和应用范围:查表
9-4 链传动的工作情况分析
链传动的运动特性
当链绕在链轮上时,其链节与相应的轮齿啮合后,这一段链条将曲折成正多边形的一部分。链的平均速度
v
v
v (m/s)为
v
=
z
1
n
1
p
60
×
1000
=
z
2
n
2
p
60
×
1000
v = \frac{z_1 n_1 p}{60 \times 1000} = \frac{z_2 n_2 p}{60 \times 1000}
v=60×1000z1n1p=60×1000z2n2p
其中,
z
1
z_1
z1 、
z
2
z_2
z2 分别为主、从动链轮的齿数;
n
1
n_1
n1 、
n
2
n_2
n2 为主、从动链轮的转速,单位 r/min。
链传动平均传动比:
i
=
n
1
n
2
=
Z
2
Z
1
i = \frac{n_1}{n_2} = \frac{Z_2}{Z_1}
i=n2n1=Z1Z2
链速瞬时变化
假设主动链轮转速恒定,链传动的速度分析如下:

铰链 A 实际用于牵引链条运动的速度
v
x
v_x
vx 为
v
x
=
v
1
c
o
s
β
=
R
1
ω
1
c
o
s
β
v_x = v_1 cos\beta = R_1 \omega_1 cos\beta
vx=v1cosβ=R1ω1cosβ
- 当 β = ± φ 1 2 = ± 18 0 ∘ z 1 \beta = \pm \frac{\varphi_1}{2} = \pm \frac{180^\circ}{z_1} β=±2φ1=±z1180∘ 时,链速最低。
- 当 β = 0 \beta = 0 β=0 时,链速最高。
链速变化呈周期性,链轮转过一个链节,对应链速变化的一个周期。转速越高、齿数越少,链速变化范围越大。
铰链 A 带动链条上下运动,上下运动的链速
v
y
1
v_{y1}
vy1 也随链节周期性变化
v
y
1
=
v
1
s
i
n
β
=
R
1
ω
1
s
i
n
β
v_{y1} = v_1 sin\beta = R_1 \omega_1 sin\beta
vy1=v1sinβ=R1ω1sinβ

从动链轮上,铰链 C 沿圆周方向运动的线速度
v
2
=
R
2
ω
2
=
v
x
c
o
s
γ
v_2 = R_2 \omega_2 = \frac{v_x}{cos\gamma}
v2=R2ω2=cosγvx
由此,从动轮转速为
ω
2
=
v
x
R
2
c
o
s
γ
=
R
1
ω
1
c
o
s
β
R
2
c
o
s
γ
\omega_2 = \frac{v_x}{R_2 cos\gamma} = \frac{R_1 \omega_1 cos\beta}{R_2 cos\gamma}
ω2=R2cosγvx=R2cosγR1ω1cosβ
γ \gamma γ 在 ± 18 0 ∘ z 2 \pm \frac{180^\circ}{z_2} ±z2180∘ 内不断变化, β \beta β 也在变化,所以即使 ω 1 \omega_1 ω1 为常数, ω 2 \omega_2 ω2 也是周期性变化的。
链传动瞬时传动比
i
=
ω
1
ω
2
=
R
2
cos
γ
R
1
cos
β
i = \frac{\omega_1}{\omega_2} = \frac{R_2 \cos \gamma}{R_1 \cos \beta}
i=ω2ω1=R1cosβR2cosγ
链传动多边形效应
链传动的传动比变化与链条绕在链轮上的多边形特征有关。
链传动的动载荷
链速变化引起的惯性力:
F
d
1
=
m
a
c
F_{d1} = ma_c
Fd1=mac
m:紧边链条的质量,kg
a
c
a_c
ac:链条变速运动的加速度,m/s²
视主动链轮匀速转动,当
β
=
±
φ
1
2
=
±
18
0
∘
z
1
\beta = \pm \frac{\varphi_1}{2} = \pm \frac{180^\circ}{z_1}
β=±2φ1=±z1180∘ 时,最大加速度
(
a
c
)
max
(a_c)_{\max}
(ac)max 为:
(
a
c
)
max
=
−
R
1
ω
1
2
s
i
n
(
±
180
°
z
1
)
=
±
ω
1
2
p
2
(a_c)_{\max} = -R_1 \omega_1^2 sin(\pm \frac{180°}{z_1}) = \pm \frac{\omega_1^2 p}{2}
(ac)max=−R1ω12sin(±z1180°)=±2ω12p
从动链轮因角加速度引起的惯性力为:
F
d
2
=
J
R
2
d
ω
2
d
t
F_{d2} = \frac{J}{R_2} \frac{d\omega_2}{dt}
Fd2=R2Jdtdω2
J:从动系统转化到从动链轮轴上的转动惯量,kg · m²
ω
2
ω_2
ω2:从动链轮的角速度,rad/s
链轮转速越高、节距越大、齿数越少,则惯性力越大,相应动载荷越大;同时链条沿垂直方向的变速运动也会产生一定的动载荷
链节和链轮啮合瞬间的相对速度,也将引起冲击和振动:节距越大、链轮转速越高,冲击越严重
链传动的受力分析
链条安装时应有一定的张紧力——通过使链条保持适当的垂度所产生的悬垂拉力
紧边拉力与松边拉力:
F
1
=
F
e
+
F
c
+
F
f
F_1 = F_e + F_c + F_f
F1=Fe+Fc+Ff
F
2
=
F
c
+
F
f
F_2 = F_c + F_f
F2=Fc+Ff
F
e
F_e
Fe: 有效圆周力
F
c
F_c
Fc: 离心力引起的拉力
F
f
F_f
Ff: 悬垂拉力
有效圆周力:
F
e
=
1000
P
v
F_e = 1000 \frac{P}{v}
Fe=1000vP
P:传递的功率,kW
v:链速,m/s
离心力引起的拉力:
F
c
=
q
v
2
F_c = qv^2
Fc=qv2
q 为链条单位长度的质量,kg/m
悬垂拉力:
F
f
=
m
a
x
(
F
f
′
,
F
f
′
′
)
F_f = max(F_f', F_f'')
Ff=max(Ff′,Ff′′)
其中:
F
f
′
=
K
f
q
a
×
1
0
−
2
F_f' = K_f qa \times 10^{-2}
Ff′=Kfqa×10−2
F
f
′
′
=
(
K
f
+
s
i
n
α
)
q
a
×
1
0
−
2
F_f'' = (K_f + sin\alpha) qa \times 10^{-2}
Ff′′=(Kf+sinα)qa×10−2
a: 链传动的中心距,mm
K
f
K_f
Kf: 垂度系数,查表
9-5 滚子链传动的设计计算
链传动的失效形式
(1)链的疲劳破坏
- 经过一定循环次数后,链板将会因疲劳而断裂
- 套筒和滚子表面将会因冲击而出现疲劳点蚀
- 链条的疲劳强度为决定链传动承载能力的主要因素
(2)链条铰链的磨损
- 使链节距增大,链条总长度增加
- 使链的松边垂度发生变化
- 增大运动的不均匀性和动载荷,引起跳齿
(3)链条铰链的胶合
- 胶合在一定程度上限制了链传动的极限转速
(4)链条的静力破坏
- 当链速较低时(v < 0.6 m/s),如果链条负载不增加而变形持续增加,即认为链条正在被破坏
- 导致链条变形持续增加的最小负载将限制链条能够承受的最大载荷
链传动的额定功率
- 极限功率曲线:

1.在润滑良好、中等速度下,链传动的主要承载能力主要取决于链板的疲劳强度
2.随着转速提高,链传动的动载荷增大,传动能力主要取决于滚子和套筒的冲击疲劳强度
3.当转速很高时,胶合将限制链传动的承载能力
- 额定功率曲线:采用额定功率 P c P_c Pc 来限制链传动的实际工作能力

通过试验确定额定功率曲线,一个试验条件:查表
当链传动的工作条件与试验条件不同时,额定功率应予以修正。修正时考虑工作情况、主动链轮齿数、链传动的排数
链传动的参数选择
链轮齿数 z 1 z_1 z1 和 z 2 z_2 z2
- “小链轮不宜太小,大链轮不宜太大”。
链轮齿数过少的缺点:
- 增加运动的不均匀性和动载荷
- 链条在进入和退出啮合时,链节间的相对转角增大
- 链传动的圆周力增大,从整体上加速铰链和链轮的磨损
- 链轮最小齿数 z m i n = 9 z_{min} = 9 zmin=9
- z 1 ≥ 17 z_1 \geq 17 z1≥17 (一般)
- z 2 ≥ 25 z_2 \geq 25 z2≥25 (高速传动或承受冲击载荷的链传动)、链轮应淬硬
链轮齿数过多的缺点:
- 增大传动总体尺寸
- 易发生跳链、脱链:链节增长量 Δp 一定时,链轮齿数越多,链轮上一个链节所对的圆心角就越小,铰链所在圆的直径的增加量 Δd 越大,铰链会更接近齿顶(如图),从而增大跳链和脱链机会
- z m a x ≤ 150 z_{max} ≤ 150 zmax≤150,一般 z ≤ 114

常取链轮齿数为奇数,并尽可能与链节数互质:链节数通常为偶数,这样可以使链条和链轮磨损均匀
传动比 i i i
- 一般 i ≤ 6 i \leq 6 i≤6
- 2 ≤ i ≤ 3.5 2 \leq i \leq 3.5 2≤i≤3.5。
- 链条在小链轮上的包角不应小于 12 0 ∘ 120^\circ 120∘。
中心距
a
a
a
中心距过小的缺点:
- 单位时间内链条的绕转次数增多,链条曲伸次数和应力循环次数增多,加剧链条的磨损和疲劳
- 链条在小链轮上的包角变小,每个轮齿所受的载荷增大,易出现跳齿和脱链现象
中心距太大的缺点:松边垂度过大,传动时造成松边颤动
中心距取值推荐
| 情况 | 中心距取值公式 |
|---|---|
| 无其他限制 | a 0 = ( 30 ∼ 50 ) p a_0 = (30 \sim 50) p a0=(30∼50)p |
| 无其他限制,无张紧装置或托板 | a 0 max = 80 p a_{0\max} = 80 p a0max=80p |
| 有张紧装置或托板 | a 0 max a_{0\max} a0max 可以大于 80 |
| 中心距不能调整 | a 0 max ≈ 30 p a_{0\max} \approx 30p a0max≈30p |
链的节距
p
p
p 和排数
节距大可以提高承载能力
节距大的缺点:
- 总体尺寸增大
- 多边形效应显著
- 振动、冲击、噪声更严重
| 工作情况 | 链的节距排数选择 | 理由 |
|---|---|---|
| —— | 较小节距单排链 | 结构紧凑、延长寿命 |
| 速度高、功率大 | 小节距多排链 | —— |
| 中心距小、传动比大 | 小节距单排链 | 经济 |
| 中心距大、传动比小 | 大节距多排链 | 经济 |
滚子链传动的设计计算
已知条件
- 链传动的工作条件。
- 传动位置与总体尺寸限制。
- 所需传递的功率 P P P。
- 主、从动链轮转速 n 1 n_1 n1、 n 2 n_2 n2 或传动比 i i i。
设计内容
- 链条型号、链节数 L p L_p Lp、排数。
- 链轮齿数 z 1 z_1 z1、 z 2 z_2 z2。
- 链轮的材料、几何尺寸。
- 链传动的中心距 a a a。
- 压轴力 F p F_p Fp。
- 润滑方式、张紧方式等。
设计步骤和方法
(1)选择链轮齿数
z
1
z_1
z1、
z
2
z_2
z2 和确定传动比
i
i
i
链轮齿数一般为 17 ~ 114
传动比:
i
=
z
2
z
1
i = \frac{z_2}{z_1}
i=z1z2
(2)计算当量的单排链计算功率
P
c
a
P_{ca}
Pca
P
c
a
=
K
A
K
z
K
p
P
P_{ca} = \frac{K_A K_z}{K_p} P
Pca=KpKAKzP
| 宇母符号 | 含义 |
|---|---|
| K A K_A KA | 工作情况系数,需查表获取 |
| K z K_z Kz | 主动链轮齿数系数, K z = ( 19 Z 1 ) 1.08 K_z = (\frac{19}{Z_1})^{1.08} Kz=(Z119)1.08 |
| K p K_p Kp | 多排链系数,对于双排链取值 1.7 1.7 1.7 ,三排链取值 2.5 2.5 2.5 |
| P P P | 传递的功率,单位为千瓦(kW) |
(3)确定链条型号和节距
p
p
p
链条型号:查表(根据当量的单排链计算功率
P
c
a
P_{ca}
Pca 、单排链额定功率
P
c
P_c
Pc 、、主动链轮转速
n
1
n_1
n1)
确定链条节距 p p p:查表
(4)计算链节数和中心距
初选中心距
a
0
=
(
30
∼
50
)
p
a_0 = (30 \sim 50) p
a0=(30∼50)p,按下式计算链节数
L
p
0
L_{p0}
Lp0:
L p 0 = 2 a 0 p + z 1 + z 2 2 + ( z 2 − z 1 2 π ) 2 p a 0 L_{p0} = \frac{2a_0}{p} + \frac{z_1 + z_2}{2} + \left(\frac{z_2 - z_1}{2\pi}\right)^2 \frac{p}{a_0} Lp0=p2a0+2z1+z2+(2πz2−z1)2a0p
为避免使用过渡链节,应将计算出的链节数 L p 0 L_{p0} Lp0 圆整为偶数 L p L_p Lp。
链传动最大中心距为:
a max = f 1 p [ 2 L p − ( z 1 + z 2 ) ] a_{\max} = f_1 p \left[2L_p - \left(z_1 + z_2\right)\right] amax=f1p[2Lp−(z1+z2)]
其中, f 1 f_1 f1 为中心距计算系数,需查表获得。
特别地,当两链轮的齿数相等(即 z = z 1 = z 2 z = z_1 = z_2 z=z1=z2 )时,链传动的最大中心距为:
a max = p ( L p − z 2 ) a_{\max} = p \left(\frac{L_p - z}{2}\right) amax=p(2Lp−z)
(5)计算链速,确定润滑方式
链的平均速度
v
v
v (m/s)的计算公式为:
v
=
z
1
n
1
p
60
×
1000
=
z
2
n
2
p
60
×
1000
v = \frac{z_1 n_1 p}{60 \times 1000} = \frac{z_2 n_2 p}{60 \times 1000}
v=60×1000z1n1p=60×1000z2n2p
| 宇母符号 | 含义 |
|---|---|
| z 1 z_1 z1, z 2 z_2 z2 | 主、从动链轮的齿数 |
| n 1 n_1 n1, n 2 n_2 n2 | 主、从动链轮的转速,单位为每分钟转数(r/min) |
润滑方式应根据具体条件查表确定。
(6)计算链传动作用在轴上的压轴力 F p F_p Fp
压轴力
F
p
F_p
Fp 的计算公式为:
F
p
≈
K
F
p
⋅
F
e
F_p \approx K_{Fp} \cdot F_e
Fp≈KFp⋅Fe
| 宇母符号 | 含义 |
|---|---|
| F e F_e Fe | 有效圆周力,单位为牛顿(N) |
| K F p K_{Fp} KFp | 压轴力系数,对于水平传动取值 1.15 1.15 1.15;对于垂直传动取值 1.05 1.05 1.05 |
9-6 链传动的布置、张紧、润滑与防护
链传动的布置
链轮必须位于铅垂面内,两链轮共面
中心线可以水平或倾斜,尽量不要处于铅锤位置
紧边在上,松边在下
具体布置:查表
链传动的张紧
目的:避免在链条的松边垂度过大时产生啮合不良和链条的振动现象、增加链条与链轮的啮合包角
张紧方法:
- 调节中心距(中心距可调时)
- 张紧轮
-
- 链轮或滚轮
-
- 直径与小链轮的直径相近
-
- 自动张紧(弹簧、吊重等)或定期张紧(螺旋、偏心等调整装置)
- 压板、托板
链传动的润滑
润滑作用:缓和冲击、减轻磨损、延长链条使用寿命
推荐润滑方式:查表
链传动的防护
应用防护罩将链传动装置封闭,与灰尘隔离以保证正常润滑
第十章 齿轮传动

某车用变速箱
10-1 概述
齿轮传动优点:
- 效率高
- 结构紧凑
- 工作可靠、寿命长
- 传动比稳定
齿轮传动缺点:
- 制造及安装精度要求高
- 价格较高
- 不宜用于传动距离过大的场合
分类(按封闭程度):
(1)开式齿轮传动
- 没有防尘罩或机壳,齿轮完全暴露在外
- 外界杂物极易侵入,润滑不良,轮齿易磨损
- 只宜用于低速传动
(2)半开式齿轮传动
- 装有简单的防护罩
- 有时把大齿轮部分浸入油池中
(3)闭式齿轮传动
- 装在经过精确加工且封闭严密的箱体(机匣)内
- 润滑防护等条件最好
- 多用于重要的场合(汽车、机床、航空发动机……)
10-2 齿轮传动的失效形式及设计准则
失效形式
GB/T 3481-1997 齿轮轮齿磨损和损伤术语
硬齿面齿轮:齿轮工作面硬度 > 350 HBS 或 38 HRC
软齿面齿轮:齿轮工作面硬度 ≤ 350 HBS 或 38 HRC
一般地说,齿轮传动的失效主要是轮齿的失效,这里只简单介绍常见的五种轮齿失效形式
轮齿折断
折断情况:
- 正常工况下,齿根的循环弯曲应力超过其疲劳极限时,将在齿根处产生疲劳裂纹,裂纹逐步扩展致使轮齿疲劳折断
- 突加载荷作用下过载折断
- 严重磨损导致齿厚过分减薄,也会在名义载荷作用下发生折断
折断扩展方式:
- 齿宽较小的直齿圆柱齿轮 —— 整齿折断(从齿根沿着横向扩展)
- 齿宽较大的直齿圆柱齿轮 —— 局部折断(从齿根斜向齿顶的方向扩展)
- 斜齿圆柱齿轮、人字齿圆柱齿轮 —— 局部折断(从齿根斜向齿顶的方向扩展)
措施:
- 采用正变位齿轮,增加齿根的强度
- 使齿根过渡曲线变化更为平缓及消除加工刀痕,减小齿根应力集中
- 增大轴及支承的刚性,使轮齿接触线上的受载较为均匀
- 采用合适的热处理方法使齿芯材料具有足够的韧性
- 采用喷丸、滚压等工艺措施对齿根表层进行强化处理
齿面磨损
开式齿轮传动的主要失效形式之一
磨损引起齿廓变形和齿厚减薄,产生振动和噪声,甚至因轮齿过薄而断裂
措施:
- 采用闭式齿轮传动
- 提高齿面硬度
- 降低齿面粗糙度值
- 注意保持润滑油清洁
齿面点蚀
疲劳点蚀:
- 齿轮工作时,在循环应力、齿面摩擦力及润滑剂的反复作用下,在齿面或其表层内会产生微小的裂纹。这些裂纹继续扩展,相互连接,形成小片并脱落,在齿面上出现细碎的凹坑或麻点,从而造成齿面损伤,称为疲劳点蚀。润滑油是接触疲劳磨损的媒介
- 收敛性点蚀:新齿轮在短期工作后出现的点蚀痕迹,继续工作不再发展或反而消失。只发生在软齿面上
- 扩展性点蚀:随着工作时间的延长而继续扩展的点蚀
- 点蚀往往首先出现在靠近节线的齿根面上,然后再向其他部位扩展,靠近节线处的齿根面抵抗点蚀破坏的能力最弱
措施:
- 提高齿轮材料的硬度
- 降低表面粗糙度值
- 加注(合理限度内)高黏度的润滑油
- 减小动载荷
齿面胶合
由于齿面间未能有效地形成润滑油膜,导致齿面金属直接接触,并在随后的相对滑动中,相互粘连的金属沿着相对滑动方向相互撕扯而出现一条条划痕
齿面胶合会引起振动和噪声,导致齿轮传动性能下降,甚至失效
齿面热胶合:因摩擦导致局部温度上升、油膜破裂,造成齿面金属直接接触并相互黏着(高速重载齿轮)
齿面冷胶合:齿面间压力很高,导致油膜破裂而使金属黏着(低速重载 v < 4 m/s)
措施:
- 采用正变位齿轮
- 减小模数
- 降低齿高以减小滑动速度
- 提高齿面硬度
- 降低齿面粗糙度值
- 采用抗胶合能力强的齿轮材料
- 在润滑油中加入抗胶合能力强的极压添加剂
塑性变形
轮齿材料过软,轮齿上的载荷所产生的应力超过材料的屈服极限,则轮齿出现塑性变形
沿摩擦力作用方向发生金属塑形流动:主动轮的轮齿上,齿面金属的流动导致节线处下凹;从动轮轮齿上,齿面金属的流动导致节线处凸起
措施:
- 提高轮齿齿面硬度
- 采用高黏度的或加油极压添加剂的润滑油
其他措施
选配主、从动齿轮的材料及硬度、适当的磨合(跑合)、选用合适的润滑剂及润滑方法等
设计准则
通常只按保证齿根弯曲疲劳强度及保证齿面接触疲劳强度两准则进行设计
对高速大功率的齿轮传动,还要保证按齿面抗胶合能力的准则进行设计 (GB/T 3480-1997 渐开线圆柱齿轮承载能力计算方法)
10-3 齿轮的材料及其选择原则
齿面要硬 齿芯要韧
常用的齿轮材料
钢:
锻钢(0.15% ~ 0.6%的碳钢或合金钢)
- 经热处理后切齿的齿轮
-
- 软齿面(硬度 ≤ 350 HBW)
-
- 正火或调质处理后切齿
-
- 精度: 8 级(一般)7 级(精切)
- 需要进行精加工的齿轮
-
- 先切齿,再表面硬化处理,最后精加工
-
- 精度可达 5 级或 4 级
铸钢
- 退火、正火处理,必要时也可进行调质
- 常用于尺寸较大的齿轮
合金钢
铸铁:
- 抗冲击、耐磨性较差,抗胶合抗点蚀能力较好
- 工作平稳,速度较低,功率不大的场合
非金属材料:
- 高速、轻载、精度不高的齿轮传动
- 常用夹布胶木、尼龙等非金属材料做小齿轮,降低噪声
- 齿面硬度应为 250 ~ 350 HBW
常用的齿轮材料及其力学性能:查表
齿轮材料的选择原则
必须满足工作条件的要求
应考虑齿轮尺寸的大小、毛坯成形方式及热处理和制造工艺
正火碳钢只能用于制作在载荷平稳或轻度冲击下工作的齿轮,不能承受大的冲击载荷;调制碳钢可用于制作在中等冲击载荷下工作的齿轮
合金钢常用于制作高速、重载并在冲击载荷下工作的齿轮
飞行器中的齿轮传动要求齿轮尺寸尽可能小,应采用表面硬化处理的高强度合金钢
金属制的软齿面齿轮,配对两轮齿面的硬度差应保持为 30 ~ 50 HBW 或更多
10-4 齿轮传动的计算载荷
实际传动中,轮齿上的载荷会大于由额定功率和转速计算出来的名义法向载荷
F
n
F_n
Fn,应修正,以得到用于齿轮强度计算的计算载荷:
F
c
a
=
K
F
n
F_{ca} = K F_n
Fca=KFn
F
c
a
F_{ca}
Fca: 计算载荷
F
n
F_{n}
Fn: 轮齿上的名义法向载荷
K
K
K: 载荷系数,等于4个系数的连乘积,见下公式
K
=
K
A
K
V
K
α
K
β
K = K_A K_V K_\alpha K_\beta
K=KAKVKαKβ
使用系数 K A K_A KA
表征齿轮传动中的实际载荷受原动机和工作机特性、质量比、联轴器类型、运动状态的影响
实用值应针对设计对象通过实践确定
参考值:查表
动载系数 K V K_V KV
误差和变形导致啮合轮齿的法节
p
b
1
p_{b1}
pb1 与
p
b
2
p_{b2}
pb2 不相等,可能出现前一对齿还未退出啮合,后一对齿已经提前啮合,或前一对齿已经退出啮合一段时间,后一对齿才滞后啮合的情况,因而瞬时传动比不是定值,从动轮在运转中产生角加速度,引起动载荷或冲击

减小动载荷:提高制造精度、减小齿轮直径以降低圆周速度
齿顶修缘:
把齿顶的一小部分齿廓曲线(分度圆压力角 α = 20° 的渐开线)修整成 α > 20° 的渐开线,以减小动载荷
高速齿轮传动或齿面经硬化的齿轮,轮齿应进行修缘
齿间载荷分配系数 K α K_\alpha Kα
在啮合区中有两对(或多对)齿同时工作,两对齿承担的载荷并不相等,引入
K
α
K_\alpha
Kα 以计入这种影响
K
H
α
K_{H\alpha}
KHα 齿面接触疲劳强度计算
K
F
α
K_{F\alpha}
KFα 齿根弯曲疲劳计算
K
α
K_{\alpha}
Kα 的计算分为一般方法和简化方法,对于简化方法可查表得
齿向载荷分布系数 K β K_\beta Kβ
作用在齿面上的载荷沿接触轴线分布不均匀
先 K H β K_{H\beta} KHβ 再 K F β K_{F\beta} KFβ
齿宽系数 ϕ d = b d m 1 \phi_d = \frac{b}{d_{m1}} ϕd=dm1b,齿宽 / 平均分度圆直径
降低载荷沿接触线分布不均程度的措施:
- 增大轴、轴承及支座的刚度
- 对称地配置轴承
- 适当地限制齿轮的宽度
- 尽可能避免齿轮作悬臂布置
- 使用鼓形齿
10-5 标准直齿圆柱齿轮传动的强度计算
轮齿的受力分析
计算时忽略摩擦
为计算齿轮上的名义法向力 F n F_n Fn,(集中力代替分布力)将其在小齿轮的节圆处分解为圆周力 F t 1 F_{t1} Ft1 和径向力 F r 1 F_{r1} Fr1,然后计算
F
t
1
=
2
T
1
d
1
F_{t1} = \frac{2T_1}{d_1}
Ft1=d12T1
F
r
1
=
F
t
1
tan
(
α
)
F_{r1} = F_{t1} \tan(\alpha)
Fr1=Ft1tan(α)
F
n
=
F
t
1
cos
(
α
)
F_{n} = \frac{F_{t1}}{ \cos(\alpha)}
Fn=cos(α)Ft1
- F t 1 F_{t1} Ft1:圆周力
- F r 1 F_{r1} Fr1:径向力
- F n F_{n} Fn:法向力
- T 1 T_1 T1:小齿轮传递的扭矩,单位为牛顿毫米 N ⋅ m m N \cdot mm N⋅mm
- α \alpha α:压力角
齿根弯曲疲劳强度计算
直齿圆柱齿轮的弯曲疲劳强度条件:
σ F = σ F 0 K F Y S a Y ϵ = K F F t 1 b m Y F a Y S a Y ϵ ≤ [ σ F ] \sigma_F = \sigma_{F0} K_F Y_{Sa} Y_\epsilon = \frac{K_F F_{t1}}{bm} Y_{Fa} Y_{Sa} Y_\epsilon \leq [\sigma_F] σF=σF0KFYSaYϵ=bmKFFt1YFaYSaYϵ≤[σF]
字母符号及其含义
- K F K_F KF:弯曲疲劳强度计算的载荷系数,计算公式为 K F = K A K v ⋅ K F α ⋅ K F β K_F = K_A K_v \cdot K_{F \alpha} \cdot K_{F\beta} KF=KAKv⋅KFα⋅KFβ
- Y S a Y_{Sa} YSa:应力修正系数,需查表获取
- Y ϵ Y_{\epsilon} Yϵ:弯曲疲劳强度计算的重合度系数,计算公式如下,见下式,其中 ϵ α \epsilon_\alpha ϵα 为直齿圆柱齿轮的重合度
Y ϵ = 0.25 + 0.75 ϵ α Y_{\epsilon} = 0.25 + \frac{0.75}{\epsilon_{\alpha}} Yϵ=0.25+ϵα0.75
设计计算式:
m
≥
2
K
F
T
1
Y
ϵ
ϕ
d
z
1
2
(
Y
F
a
Y
S
a
[
σ
F
]
)
3
m \geq \sqrt[3]{\frac{2K_F T_1 Y_{\epsilon}}{\phi_d z_1^2}(\frac{Y_{Fa} Y_{Sa}}{[\sigma_F]})}
m≥3ϕdz122KFT1Yϵ([σF]YFaYSa)
齿面接触疲劳强度计算
校核式:
σ
H
=
2
K
H
T
1
ϕ
d
d
1
3
u
±
1
u
Z
H
Z
E
Z
ϵ
≤
[
σ
H
]
\sigma_H = \sqrt{\frac{2 K_H T_1}{\phi_d d_1^3} \frac{u \pm 1}{u}}Z_H Z_E Z_\epsilon \leq [\sigma_H]
σH=ϕdd132KHT1uu±1ZHZEZϵ≤[σH]
设计计算公式:
d
1
≥
2
K
H
T
1
ϕ
d
u
±
1
u
(
Z
H
Z
E
Z
ϵ
[
σ
H
]
)
2
3
d_1 \geq \sqrt[3]{\frac{2 K_H T_1}{\phi_d} \frac{u \pm 1}{u}(\frac{Z_H Z_E Z_\epsilon}{[\sigma_H]})^2}
d1≥3ϕd2KHT1uu±1([σH]ZHZEZϵ)2
齿轮传动的强度计算说明
取一对齿轮副中较弱的那个齿轮的数据代入计算
10-6 齿轮传动的精度、设计参数与许用应力
齿轮传动的精度及其选择
渐开线圆柱齿轮传动的精度分为13个等级,其中0级最高,12级最低
齿轮传动精度等级分为三个公差组(查阅互换性相关教材):
- 第Ⅰ公差组:用齿轮一转内的转角误差表示,决定齿轮传递运动的准确程度
- 第Ⅱ公差组:用齿轮一齿内的转角误差表示,决定齿轮运转的平稳程度
- 第Ⅲ公差组:用啮合区域的形状、位置和大小表示,决定齿轮载荷分布的均匀程度
选择齿轮精度等级时应从降低制造成本的角度出发,首先满足主要使用功能,然后兼顾其他要求
齿轮传动设计参数的选择
压力角 α
增大压力角,轮齿的齿厚和节点处的齿廓曲率半径都随之增加,有利于提高齿轮传动的弯曲强度和接触强度。
| 情况 | 目的 | 压力角 |
|---|---|---|
| 一般用途齿轮 | —— | α = 20° |
| 航空齿轮 | 提高航空用齿轮传动的弯曲强度及接触强度 | α = 25° |
| 重合度接近 2 的高速齿轮传动 | 增加轮齿的柔性,降低噪声和动载荷 | 16° ~ 18° |
齿数 z
齿数多的优点:
- 增加重合度
- 有利于改善齿轮传动的平稳性
- 降低齿高
- 减小齿坯尺寸
- 降低加工时的切削量
- 降低磨损及胶合的可能性
闭式齿轮传动:
z
1
=
20
∼
40
z_1 = 20 \sim 40
z1=20∼40
开式(半开式)齿轮传动:
z
1
=
17
∼
20
z_1 = 17 \sim 20
z1=17∼20
为使轮齿磨损均匀,一般使
z
1
z_1
z1 和
z
2
z_2
z2 互为质数
齿宽系数
ϕ
d
\phi_d
ϕd
在保证齿轮接触强度和弯曲强度的前提下,增加齿宽系数,齿轮的轴向尺寸增大,而径向尺寸减小
当对径向尺寸有严格要求时,应选择较大的齿宽系数
增大齿宽系数将增大载荷沿接触线分布的不均匀程度
| 装置状况 | 两支承相对于小齿轮作对称布置 | 两支承相对于小齿轮作不对称布置 | 小齿轮作悬臂布置 |
|---|---|---|---|
| ϕ d \phi_d ϕd | 0.9 ~ 1.4(1.2 ~ 1.9) | 0.7 ~ 1.15(1.1 ~ 1.65) | 0.4 ~ 0.6 |

标准圆柱齿轮传动的端面重合度
变位系数的选择
线图法
齿轮的许用应力
齿轮疲劳试验的条件包括:
- 中心距 a = 100 a = 100 a=100 mm
- 模数 m = 3 ∼ 5 m = 3 \sim 5 m=3∼5 mm
- 压力角 α = 20 ° \alpha = 20° α=20°
- 齿宽 b = 10 ∼ 50 b = 10 \sim 50 b=10∼50 mm
- 圆周速度 v = 10 v = 10 v=10 m/s
- 齿面微观不平度十点高度 R z = 3 μ m R_z = 3 \mu m Rz=3μm
- 齿根过渡表面微观不平度十点高度 R z = 10 μ m R_z = 10 \mu m Rz=10μm
- 齿轮精度等级为 4 ~ 7 级的直齿圆柱齿轮副
- 齿轮材料在完全弹性范围内
- 承受脉动循环变应力,载荷系数 K H = K F = 1 K_H = K_F = 1 KH=KF=1
- 润滑剂黏度 υ 50 = 100 \upsilon_{50} = 100 υ50=100 mm²/s
- 失效概率为 1%
齿轮的许用应力
σ
\sigma
σ 计算公式为:
σ
=
K
N
σ
lim
S
\sigma = \frac{K_N \sigma_{\lim}}{S}
σ=SKNσlim
其中:
- σ lim \sigma_{\lim} σlim 为材料的疲劳极限
- K N K_N KN 为寿命系数,用于将试验齿轮的疲劳极限折算为实际齿轮的疲劳极限
- S S S 为疲劳安全系数
疲劳安全系数 S S S 的取值:
- 对接触疲劳强度 S H = 1 S_H = 1 SH=1
- 在进行齿根弯曲疲劳强度计算时取 S F = 1.25 ∼ 1.5 S_F = 1.25 \sim 1.5 SF=1.25∼1.5
- 在进行直齿锥齿轮的齿根弯曲疲劳强度计算时 S F ≥ 1.5 S_F \geq 1.5 SF≥1.5
寿命系数
K
N
K_N
KN 用于调整实际齿轮的工作应力循环次数
N
N
N 与试验齿轮循环次数
N
0
N_0
N0 的差异。实际齿轮的工作应力循环次数
N
N
N 计算公式为:
N
=
60
n
j
L
h
N = 60 n_j L_h
N=60njLh
10-7 标准斜齿圆柱齿轮传动的强度计算
轮齿的受力分析
为计算名义法向力 F n F_n Fn ,先将其在小齿轮分度圆处分解为:
- 圆周力 F t 1 F_{t1} Ft1(主动轮上与转向相反,从动轮上与转向相同)
- 径向力 F r 1 F_{r1} Fr1(各自指向轴心)
- 轴向力 F a 1 F_{a1} Fa1(右旋则右手定则,左旋则左手定则)
受力计算公式为:
{
F
t
1
=
2
T
1
d
1
F
r
1
=
F
t
1
tan
α
t
=
F
t
1
tan
α
n
cos
β
F
a
1
=
F
t
1
tan
β
F
n
1
=
F
t
1
cos
α
n
cos
β
=
F
t
1
cos
α
t
cos
β
b
\begin{cases} F_{t1} = \frac{2T_1}{d_1} \\ F_{r1} = F_{t1} \tan \alpha_t = \frac{F_{t1} \tan \alpha_n}{\cos \beta} \\ F_{a1} = F_{t1} \tan \beta \\ F_{n1} = \frac{F_{t1}}{\cos \alpha_n \cos \beta} = \frac{F_{t1}}{\cos \alpha_t \cos \beta_b} \end{cases}
⎩
⎨
⎧Ft1=d12T1Fr1=Ft1tanαt=cosβFt1tanαnFa1=Ft1tanβFn1=cosαncosβFt1=cosαtcosβbFt1
其中:
- α t \alpha_t αt 为端面压力角
- α n \alpha_n αn 为法面压力角, tan α n = tan α t cos β \tan \alpha_n = \tan \alpha_t \cos \beta tanαn=tanαtcosβ
- β \beta β 为螺旋角
- β b \beta_b βb 为基圆螺旋角, tan β b = tan β cos α 1 \tan \beta_b = \tan \beta \cos \alpha_1 tanβb=tanβcosα1
轴向力随螺旋角 β \beta β 增大而增大,故螺旋角一般限制在 8° ~ 20° 范围内。人字齿圆柱齿轮螺旋角 β \beta β 可取较大数值,15° ~ 40°。
斜齿圆柱齿轮强度的计算原理
将斜齿圆柱齿轮转化为当量的直齿圆柱齿轮进行强度计算。
齿根弯曲疲劳强度计算
斜齿圆柱齿轮的弯曲疲劳强度条件为:
σ
F
=
2
K
F
T
1
Y
F
a
Y
S
a
Y
ε
Y
β
cos
2
β
ϕ
d
m
n
3
z
1
2
≤
[
σ
F
]
\sigma_F = \frac{2 K_F T_1 Y_{Fa} Y_{Sa} Y_\varepsilon Y_\beta \cos^2 \beta}{\phi_d m_n^3 z_1^2} \leq \lbrack \sigma_F \rbrack
σF=ϕdmn3z122KFT1YFaYSaYεYβcos2β≤[σF]
Y S a Y_{Sa} YSa 应力修正系数 按照当量齿轮的齿数由表查取
Y ϵ Y_\epsilon Yϵ 弯曲疲劳强度计算的重合度系数 Y ϵ = 0.25 + 0.75 ϵ α v Y_\epsilon = 0.25 + \frac{0.75}{\epsilon_{\alpha v}} Yϵ=0.25+ϵαv0.75
Y β Y_\beta Yβ 弯曲疲劳强度计算的螺旋角系数 Y β = 1 − ϵ β β 120 ° Y_\beta = 1- \epsilon_\beta \frac{\beta}{120°} Yβ=1−ϵβ120°β
变换上式,可得设计计算公式:
m
n
≥
2
K
F
T
1
Y
ε
Y
β
cos
2
β
ϕ
d
z
1
2
Y
F
a
Y
S
a
[
σ
F
]
3
m_n \geq \sqrt[3]{\frac{2K_F T_1Y_\varepsilon Y_\beta \cos^2 \beta}{\phi_d z_1^2} \frac{Y_{Fa}Y_{Sa}}{\lbrack \sigma_F \rbrack}}
mn≥3ϕdz122KFT1YεYβcos2β[σF]YFaYSa
齿面接触疲劳强度计算
斜齿圆柱齿轮的接触疲劳强度条件为:
σ
H
=
2
K
H
T
1
ϕ
d
d
1
3
u
±
1
u
Z
H
Z
E
Z
ε
Z
β
≤
[
σ
H
]
\sigma_H = \sqrt{\frac{2 K_H T_1}{\phi_d d_1^3} \frac{u \pm 1}{u}} Z_H Z_E Z_\varepsilon Z_\beta \leq \lbrack \sigma_H \rbrack
σH=ϕdd132KHT1uu±1ZHZEZεZβ≤[σH]
Z
H
Z_H
ZH: 标准斜齿圆柱齿轮的区域系数
Z
H
=
a
c
o
s
β
b
c
o
s
α
t
s
i
n
α
t
Z_H = \sqrt{\frac{acos\beta_b}{cos\alpha_t sin\alpha_t}}
ZH=cosαtsinαtacosβb
Z
β
Z_\beta
Zβ: 接触疲劳强度计算的螺旋角系数
Z
β
=
c
o
s
β
Z_\beta = \sqrt{cos\beta}
Zβ=cosβ
变换上式,可得设计计算公式:
d
1
≥
2
K
H
T
1
ϕ
d
u
±
1
u
(
Z
H
Z
E
Z
ε
Z
β
[
σ
H
]
)
2
3
d_1 \geq \sqrt[3]{\frac{2K_H T_1}{\phi_d} \frac{u \pm 1}{u}(\frac{Z_H Z_E Z_\varepsilon Z_\beta}{\lbrack \sigma_H \rbrack})^2}
d1≥3ϕd2KHT1uu±1([σH]ZHZEZεZβ)2
10-8 标准直齿锥齿轮传动的强度计算

设计参数
以 大端 为标准值,规定以齿宽中点处的当量齿轮作为计算模型:
- 模数 m m = m ( 1 − 0.5 ϕ R ) m_m = m(1 - 0.5 \phi_R) mm=m(1−0.5ϕR)
- 中心距 d m = d ( 1 − 0.5 ϕ R ) d_m = d(1 - 0.5 \phi_R) dm=d(1−0.5ϕR)
- 高度 h m = h ( 1 − 0.5 ϕ R ) h_m = h(1 - 0.5 \phi_R) hm=h(1−0.5ϕR)
- 当量齿宽 d m v = d m cos δ = d ( 1 − 0.5 ϕ R ) cos δ d_{mv} = \frac{d_m}{\cos \delta} = \frac{d(1 - 0.5 \phi_R)}{\cos \delta} dmv=cosδdm=cosδd(1−0.5ϕR)
- 当量齿数 z v = z cos δ z_v = \frac{z}{\cos \delta} zv=cosδz
- 齿轮比
u
v
=
(
z
v
2
z
v
1
)
2
=
u
2
u_v = \left(\frac{z_{v2}}{z_{v1}}\right)^2 = u^2
uv=(zv1zv2)2=u2

轮齿的受力分析
计算时忽略摩擦,将名义法向力 F n F_n Fn 分解为:
- 圆周力 F t 1 F_{t1} Ft1
- 径向力 F r 1 F_{r1} Fr1(指向轴)
- 轴向力 F a 1 F_{a1} Fa1(指向大端)
计算公式如下:
{
F
t
1
=
2
T
1
d
m
1
F
r
1
=
F
t
1
tan
(
α
)
cos
(
δ
1
)
F
a
1
=
F
t
1
tan
(
α
)
sin
(
δ
1
)
F
n
=
F
t
1
cos
(
α
)
\begin{cases} F_{t1} = \frac{2T_1}{d_{m1}} \\ F_{r1} = F_{t1} \tan(\alpha) \cos(\delta_1) \\ F_{a1} = F_{t1} \tan(\alpha) \sin(\delta_1) \\ F_n = \frac{F_{t1}}{\cos(\alpha)} \end{cases}
⎩
⎨
⎧Ft1=dm12T1Fr1=Ft1tan(α)cos(δ1)Fa1=Ft1tan(α)sin(δ1)Fn=cos(α)Ft1
齿根弯曲疲劳强度计算

直齿锥齿轮的弯曲疲劳强度条件为:
σ F = 4 K F T 1 Y F a Y S a Y ε ϕ R ( 1 − 0.5 ϕ R ) 2 m 3 z 1 2 u 2 + 1 ≤ [ σ F ] \sigma_F = \frac{4 K_F T_1 Y_{Fa} Y_{Sa} Y_\varepsilon}{\phi_R (1 - 0.5 \phi_R)^2 m^3 z_1^2 \sqrt{u^2 + 1}} \leq \lbrack \sigma_F \rbrack σF=ϕR(1−0.5ϕR)2m3z12u2+14KFT1YFaYSaYε≤[σF]
变换上式,可得设计计算公式:
m ≥ 4 K F T 1 Y ε ϕ R ( 1 − 0.5 ϕ R ) 2 z 1 2 u 2 + 1 Y F a Y S a [ σ F ] 3 m \geq \sqrt[3]{\frac{4 K_F T_1 Y_\varepsilon}{\phi_R (1 - 0.5 \phi_R)^2 z_1^2 \sqrt{u^2 + 1}} \frac{Y_{Fa} Y_{Sa}}{\lbrack \sigma_F \rbrack}} m≥3ϕR(1−0.5ϕR)2z12u2+14KFT1Yε[σF]YFaYSa
齿面接触疲劳强度计算
齿面接触疲劳强度条件式为:
σ H = 4 K H T 1 ϕ R ( 1 − 0.5 ϕ R ) 2 d 1 3 u Z H Z E Z ε ≤ [ σ H ] \sigma_H = \sqrt{\frac{4 K_H T_1}{\phi_R (1 - 0.5\phi_R)^2 d_1^3 u}} Z_H Z_E Z_\varepsilon \leq \lbrack \sigma_H \rbrack σH=ϕR(1−0.5ϕR)2d13u4KHT1ZHZEZε≤[σH]
变换上式,可得设计计算公式:
d 1 ≥ 4 K H T 1 ϕ R ( 1 − 0.5 ϕ R ) 2 u ( Z H Z E Z ε [ σ H ] ) 2 3 d_1 \geq \sqrt[3]{\frac{4K_H T_1}{\phi_R (1 - 0.5 \phi_R)^2 u}(\frac{Z_H Z_E Z_\varepsilon}{\lbrack \sigma_H \rbrack})^2} d1≥3ϕR(1−0.5ϕR)2u4KHT1([σH]ZHZEZε)2
重合度系数 Z ε Z_\varepsilon Zε 按当量齿轮计算。
曲齿锥齿轮传动简介
圆弧齿(格里森制齿轮)
延伸外摆线齿(奥里康制齿轮)
10-9 变位齿轮传动强度计算概述
等变位(高度变位): x Σ = 0 , x 1 = − x 2 ≠ 0 x_\Sigma = 0, x_1 = - x_2 \neq 0 xΣ=0,x1=−x2=0
不等变位(角度变位): x Σ ≠ 0 x_\Sigma \neq 0 xΣ=0
优点:避免根切,配凑中心距,提高接触疲劳强度、弯曲疲劳强度、抗胶合能力和耐磨损能力
变位系数的具体数值一般根据设计目的和约束条件而定
计算变位齿轮传动强度计算要点:
- 在计算变位齿轮的齿根弯曲应力时,变位主要影响齿形系数、齿根应力修正系数和重合度系数
- 在计算齿面接触应力时,变位主要影响区域系数和重合度系数
- 锥齿轮传动通常按等变位齿轮传动设计
10-10 齿轮的结构设计
齿轮轴
当齿轮的轴直径与轴径相仿时,应将齿轮和轴做成一体而成为齿轮轴。齿轮的键槽底部到齿根圆的距离表示为
e
e
e。
- 圆柱齿轮: e < 2 m t e < 2 m_t e<2mt
- 锥齿轮: e < 1.6 m e < 1.6 m e<1.6m
其中, m t m_t mt 为模数。
齿轮形式
齿轮形式的选择依据齿顶圆直径
d
a
d_a
da 的大小:
- d a ≤ 160 d_a \leq 160 da≤160 mm:实心式
- 160 160 160 mm ≤ d a ≤ 500 \leq d_a \leq 500 ≤da≤500 mm:腹板式
- 400 400 400 mm < d a < 1000 < d_a < 1000 <da<1000 mm:轮辐式(截面为“十”字形)
- d a ≥ 300 d_a \geq 300 da≥300 mm,铸造锥齿轮:带加强肋的腹板式
对于尺寸较大的圆柱齿轮,可做成组装齿圈式齿轮:齿圈用钢,轮芯用铸铁或铸钢。
齿轮和轴连接
齿轮与轴的连接方式取决于使用情况:
- 一般情况:单键连接
- 齿轮转速较高:花键或双键连接
- 在轴上滑移的齿轮:花键或两个导向键连接
10-11 齿轮传动的润滑
齿轮啮合面间加注润滑剂,避免金属直接接触,减小摩擦损失,散热,防腐蚀
齿轮传动的润滑方式
开式、半开式、速度较低的闭式齿轮传动:人工做周期性加油润滑
闭式齿轮传动:浸油润滑、喷油润滑
浸油润滑:
- 齿轮圆周速度 v < 12 m/s
- 对圆柱齿轮:浸入油中深度不宜超过一个齿高,不宜小于 10 mm
- 对锥齿轮:应浸入全齿宽,至少应浸入齿宽的一半
- 对多级齿轮传动:带油轮
- 油池中油量取决于齿轮传递功率;对单级齿轮传动,每千瓦功率需油量0.35 ~ 0.7 L;多级传动需油量按级数成倍增加
喷油润滑:
- 由油泵或中心供油站以一定的压力供油,借喷嘴将润滑油喷到轮齿的啮合面上
- v > 25 m/s 时,喷嘴应位于轮齿啮出的一边,以便润滑油冷却轮齿
润滑剂的选择
润滑油或润滑脂
牌号选取:查表
10-12 圆弧齿圆柱齿轮传动简介
圆弧齿轮传动啮合轮齿的综合曲率半径 h 0 Σ h_{0\Sigma} h0Σ较大,轮齿具有较高的接触强度
圆弧齿轮传动具有良好的磨合性能
圆弧齿轮传动没有根切现象,估齿数可以少到 6 ~ 8
圆弧齿轮不能做成直齿,并为确保传动的连续性,必须具有一定的齿宽
圆弧齿轮传动对中心距及切齿深度的精度要求较高
第十一章 蜗杆传动

在交错轴间传递运动和动力的一种传动机构
11-1 蜗杆传动的类型
圆柱蜗杆传动
按照国家标准GB/T 10089-2018,圆柱蜗杆、蜗轮精度分类如下:
端面 —— 垂直于蜗杆轴线平面
轴面 —— 包含轴线的平面
阿基米德蜗杆 (ZA)
- 端面齿廓:阿基米德螺旋线
- 轴向齿廓:直线
- 齿形角: α 0 = 2 0 ∘ \alpha_0 = 20^\circ α0=20∘
法向直廓蜗杆 (ZN)
- 端面齿廓:延伸渐开线
- 法面齿廓:直线
渐开线蜗杆 (ZI)
- 端面齿廓:渐开线
- 相当于一个少齿数(齿数等于蜗杆头数)、大螺旋角的渐开线斜齿圆柱齿轮
锥面包络圆柱蜗杆 (ZK)
- 非线性螺旋齿面蜗杆
圆弧圆柱蜗杆 (ZC)
- 特点:效率高,承载能力高,体积小,质量小,结构紧凑
环面蜗杆传动
- 蜗杆体在轴向的外形是以凹圆弧为母线所形成的旋转曲面
锥蜗杆传动
特点:
- 同时接触的点数较多,重合度大
- 传动比范围大(10 ~ 360)
- 承载能力和效率较高
- 侧隙便于控制和调整
- 能作离合器使用
- 可节约有色金属
- 制造安装简便,工艺性好
- 不对称性,因而正、反转时受力不同,承载能力和效率不同
蜗杆传动类型选择的原则
1.重载、高速、要求效率高、精度高的重要传动,可选用圆弧圆柱蜗杆(ZC 蜗杆)传动或包络环面蜗杆传动
2.传动效率高、蜗杆不磨削的大功率传动,可选用环面蜗杆传动
3.速度高、精密、蜗杆头数较多、加工工艺简单,可选用渐开线圆柱蜗杆(ZI 蜗杆)传动、锥面包络蜗杆(ZK 蜗杆)传动或法向直廓蜗杆(ZN 蜗杆)传动
4.载荷较小、速度较低、精度要求不高或不太重要的传动,要求蜗杆加工简单时,可选用阿基米德螺圆柱蜗杆(ZA 蜗杆)传动
5.要求自锁的低速、轻载的传动,可选用单头阿基米德圆柱蜗杆(ZA 蜗杆)传动
11-2 普通圆柱蜗杆传动的基本参数及几何尺寸计算
在中间平面上,普通圆柱蜗杆传动相当于齿条与齿轮的啮合传动。故在设计蜗杆传动时,取中间平面上的参数和尺寸为基准,并沿用齿轮传动的计算关系。
普通圆柱蜗杆传动的基本参数及其选择
模数 m m m 和压力角 α \alpha α
- m a 1 = m t 2 = m m_a1 = m_{t2} = m ma1=mt2=m
- α a 1 = α t 2 \alpha_{a1} = \alpha_{t2} αa1=αt2
ZA 蜗杆轴向压力角 α a \alpha_a αa 为标准值(20°)
ZN、ZI、ZK 蜗杆法向压力角 α n \alpha_n αn 为标准值(20°)
t a n α a = t a n α n c o s γ tan\alpha_a = \frac{tan\alpha_n}{cos\gamma} tanαa=cosγtanαn
蜗杆的分度圆直径 d 1 d_1 d1
蜗杆的直径系数 q = d 1 m q = \frac{d_1}{m} q=md1
d 1 d_1 d1 与 q 有标准值,以限制蜗轮滚刀的数目与便于标准化
常用的标准模数 m 和蜗杆分度圆直径 d 1 d_1 d1:查表
蜗杆头数
z
1
z_1
z1
蜗杆头数少:传动比可以较大,效率低
蜗杆头数多:效率高,加工困难
- 常取 1、2、4、6
导程角
γ
\gamma
γ
tan
(
γ
)
=
p
z
π
d
1
=
z
1
p
a
π
d
1
=
z
1
m
d
1
=
z
1
q
\tan(\gamma) = \frac{p_z}{\pi d_1} = \frac{z_1 p_a}{\pi d_1} = \frac{z_1 m}{d_1} = \frac{z_1}{q}
tan(γ)=πd1pz=πd1z1pa=d1z1m=qz1
p
z
p_z
pz 蜗杆导程,
p
z
=
z
1
p
a
p_z = z_1 p_a
pz=z1pa
p
a
p_a
pa 蜗杆轴向齿距
传动比
i
i
i 与齿数比
u
u
u
i
=
n
1
n
2
i = \frac{n_1}{n_2}
i=n2n1
u
=
z
2
z
1
u = \frac{z_2}{z_1}
u=z1z2
当蜗杆为主动时,i = u
蜗轮齿数
z
2
z_2
z2
蜗杆传动的标准中心距 a
a = 1 2 ( d 1 + d 2 ) = 1 2 ( d 1 + z 2 m ) a = \frac1 2(d_1 + d_2) = \frac1 2 (d_1 + z_2 m) a=21(d1+d2)=21(d1+z2m)
蜗杆传动的几何尺寸计算
11-3 普通圆柱蜗杆传动承载能力计算
蜗杆传动的失效形式、设计准则及常用材料
蜗杆传动的受力分析
蜗杆传动强度计算
设计式:
m
2
d
1
≥
1.53
K
T
2
z
2
[
σ
F
]
Y
F
a
2
Y
β
m^2 d_1 \geq \frac{1.53 K T_2}{z_2 [\sigma_F]} Y_{Fa2} Y_\beta
m2d1≥z2[σF]1.53KT2YFa2Yβ
蜗杆的刚度计算
最大挠度
y
y
y:
y
=
F
t
1
2
+
F
r
1
2
48
E
I
L
′
3
≤
[
y
]
y = \frac{\sqrt{F_{t1}^2 + F_{r1}^2}}{48 EI} {L^{'}}^3 \leq [y]
y=48EIFt12+Fr12L′3≤[y]
| 字母符号 | 含义 | 单位 |
|---|---|---|
| F t 1 F_{t1} Ft1 | 蜗杆所受的圆周力 | N |
| F r 1 F_{r1} Fr1 | 蜗杆所受的径向力 | N |
| E E E | 蜗杆材料的弹性模量 | MPa |
| I I I | 蜗杆危险截面的惯性矩 | mm^4 |
| L ′ L' L′ | 蜗杆两端支承间的跨距,初步计算可选取 L ′ ≈ 0.9 d 2 L' \approx 0.9d_2 L′≈0.9d2 | mm |
| [ y ] [y] [y] | 许用最大挠度, [ y ] = d 1 1000 [y] = \frac{d_1}{1000} [y]=1000d1 | mm |
普通圆柱蜗杆传动的精度等级及其选择
GB/T 10089-2018 圆柱蜗杆、蜗轮精度中规定了12个精度等级(1级最高),三个公差组
6 级精度:中等精度机床的分度机构、发动机调节系统及机械师读数装置的精密传动。允许的蜗轮圆周速度
v
2
>
5
v_2 > 5
v2>5 m/s
7 级精度:运输和一般工业中的中等速度(
v
2
<
7.5
v_2 < 7.5
v2<7.5 m/s)的动力传动
8 级精度:每昼夜只有短时工作的次要的低速(
v
2
≤
3
v_2 \leq 3
v2≤3 m/s)传动
11-4 圆弧圆柱蜗杆传动设计计算
概述
C蜗杆传动比普通圆柱蜗杆传动的承载能力大,传动效率高,使用寿命长,有逐渐代替后者的趋势
传动特点
可以实现交错轴之间的传动,蜗杆能安装在蜗轮的上、下方或侧面
- 传动比范围大,可实现 1:100 的大传动比传动
- 蜗杆与蜗轮的齿廓呈凹凸啮合,接触线与相对滑动速度方向间的夹角大,有利于液体动力润滑油膜的形成,抗胶合能力强,承载能力大
- 当蜗杆主动时,啮合效率可达 95% 以上,比普通圆柱蜗杆传动的啮合效率提高 10% ~ 20%
- 中心距的偏差对蜗杆传动的承载能力影响较大(对中心距偏差较敏感)
蜗杆传动的效率
- 啮合摩擦损耗 η 1 \eta_1 η1
- 轴承摩擦损耗 η 2 \eta_2 η2
- 溅油损耗 η 3 \eta_3 η3
当蜗杆主动时:
η
1
=
tan
(
γ
)
tan
(
γ
+
φ
v
)
\eta_1 = \frac{\tan(\gamma)}{\tan(\gamma + \varphi_v)}
η1=tan(γ+φv)tan(γ)
圆弧圆柱蜗杆传动强度计算
11-5 普通圆柱蜗杆传动的效率、润滑及热平衡计算
蜗杆传动的效率
- 啮合摩擦损耗 η 1 \eta_1 η1
- 轴承摩擦损耗 η 2 \eta_2 η2
- 溅油损耗 η 3 \eta_3 η3
当蜗杆主动时:
η
1
=
t
a
n
γ
t
a
n
(
γ
+
φ
v
)
\eta_1 = \frac{tan\gamma}{tan(\gamma + \varphi_v)}
η1=tan(γ+φv)tanγ
轴承摩擦与溅油摩擦功率损耗不大,一般取
η
2
η
3
=
0.95
∼
0.96
\eta_2 \eta_3 = 0.95 \sim 0.96
η2η3=0.95∼0.96
在设计之初,为近似求出蜗轮轴上的转矩 T 2 T_2 T2, η \eta η 值可如下估取:
| 蜗杆头数 z 1 z_1 z1 | 总效率 η |
|---|---|
| 1 | 0.7 |
| 2 | 0.8 |
| 4 | 0.9 |
| 6 | 0.95 |
蜗杆传动的润滑
蜗杆传动的热平衡计算
热平衡计算原因:蜗杆传动效率低发热量大,在闭式传动中若热量不能及时散逸,油温将不断升高导致润滑油稀释,进而增大摩擦损失,甚至发生胶合
计算条件:单位时间内的发热量等于同时间内的散热量
11-6 圆柱蜗杆和蜗轮的结构设计
参考
1、机械设计(邱宣怀.第4版)
2、muzing–《机械设计》知识点整理
3、机械设计 主编 濮良贵 陈国定 吴立言 [第十版] 【西北工业大学】



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










