九轴MARG传感器梯度下降法

介绍

本文主要是对Madgwick在2010年发表的文章《An efficient orientation filter for inertial and inertial/magnetic sensor arrays》进行分析，讨论Madgwick所提出的梯度下降法在四轴姿态求解四元数更新中的实用性。

四元数求解姿态角

在空间中，一个刚体由一个位置到另一个位置的表现形式常用的有两种。
一种是欧拉角，将刚体分别绕负Z轴旋转航向角φ角，再绕正X轴旋转滚转角θ角，最后绕正Y轴旋转俯仰角γ角，可以与目的地位置的刚体重合。


另一种是旋转矢量表示法，在空间中可以找到一根轴r，沿着这根轴，刚体锥面旋转θ角，与目的地位置的刚体重合。

设想一下，刚体在整个过程中不动，动的是刚体所在的坐标系，即在刚体所在的坐标系中，刚体是保持静止的，刚体所在坐标系相对于惯性系有运动，因此在惯性系中看来，刚体的坐标也发生了变化。对应于四轴飞行器，其所在坐标系被称为机体坐标系
b系（之后简称b系），而惯性系被称为游移方位坐标系p系（之后简称p系，若为指北方位，则p系与导航坐标系重合，若为游移方位，则与导航系有个游移角偏差），飞行器姿态的变化可以看作是b系相对于p系的运动。
与刚体运动表现形式相同，坐标系的运动也一样，初始时，b系与p系保持一致，即四轴在b系与p系的坐标是相同的，用欧拉角来说就是航向角、滚转角和俯仰角均为0，用旋转矢量来说是旋转轴可任取，旋转角度为0。
一切在四轴动起来之后发生变化。
欧拉角在坐标变化中演变成了旋转矩阵。

旋转矢量用四元数来进行数学表达，可在图中找到旋转轴与旋转角度的对应关系。

在进行下一步的计算前需要对四元数的运算有所了解。
范数：

乘法（不可逆）：

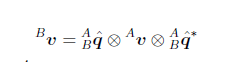
在下面的图中，Bv是描述在B系中的向量v，Av是描述在A系中的向量v, ABq是指描述B系相对于A系运动的四元数，Av左乘四元数q右乘q的共轭即将向量v所在的坐标系由A系转到了B系，四元数在这里的作用相当于矩阵R，如下图，矩阵R是经过推导所得，具体过程可参考秦永元06版《惯性导航》。

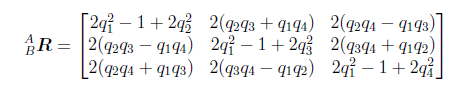
上述矩阵R就是我们前面所得到的