反向传播算法（Back Propagation)

最新推荐文章于 2024-07-10 16:47:58 发布

极光喵

最新推荐文章于 2024-07-10 16:47:58 发布

阅读量1k

点赞数 33

文章标签：算法

本文链接：https://blog.csdn.net/qq_39297053/article/details/136330657

版权

本文详细介绍了神经网络中梯度下降和反向传播的概念，强调了它们在优化权重和计算偏导数中的作用，通过实例展示了参数更新的过程以及如何利用梯度下降进行学习速率调整以减小损失。

摘要由CSDN通过智能技术生成

注意：本文引用自专业人工智能社区Venus AI

反向传播算法

梯度下降和反向传播是神经网络训练过程中两个非常重要的概念，它们密切相关。梯度下降是一种常用的优化算法，它的目标是找到一个函数的最小值或最大值。在神经网络中，梯度下降算法通过调整每个神经元的权重，以最小化网络的损失函数。损失函数是用来衡量网络的输出与真实值之间的误差。梯度下降算法的核心思想是计算损失函数对权重的偏导数，然后按照这个偏导数的反方向调整权重。

反向传播是一种有效的计算梯度的方法，它可以快速计算网络中每个神经元的偏导数。反向传播通过先正向传播计算网络的输出，然后从输出层到输入层反向传播误差，最后根据误差计算每个神经元的偏导数。反向传播算法的核心思想是通过链式法则将误差向后传递，计算每个神经元对误差的贡献。

综上所述，梯度下降和反向传播是神经网络训练过程中两个重要的概念，梯度下降算法用于优化网络的权重，反向传播算法用于计算每个神经元的偏导数。它们密切相关，并在神经网络的训练中起着重要的作用。下面用一个例子演示神经网络层参数更新的完整过程。

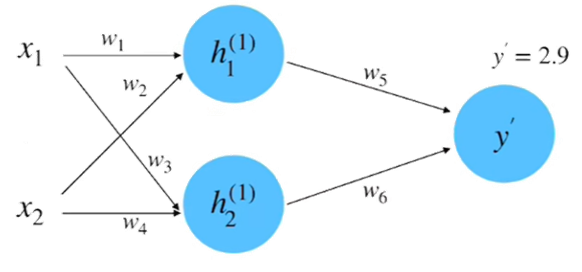
（1）初始化网络，构建一个只有一层的神经网络，如下图所示。

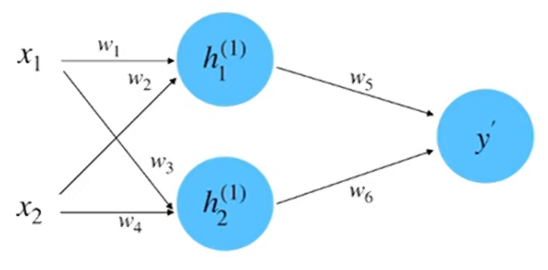
假设图 2-9 中神经网络的输入和输出的初始化为: $x_1=0.5,x_2=1.0,y=0.8$ 。参数的初始化为: $w_1=1.0,w_2=0.5,w_3=0.5,w_4=0.7,w_5=1.0,w_6=2.0$ 。
(2) 前向计算, 如下图所示。

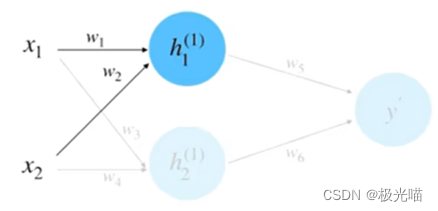
根据输入和权重计算 $h_1$ 得:

$\begin{aligned} h_{1}^{(1)}& =w_1\cdot x_1+w_2\cdot x_2 \\ &=1.0\cdot0.5+0.5\cdot1.0 \\ &=1.0 \end{aligned}$

同理, 计算 $h_2$ 等于 0.95 。将 $h_1$ 和 $h_2$ 相乘求和到前向传播的计算结果, 如下图所示。

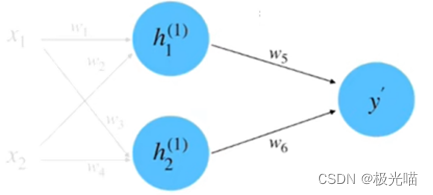
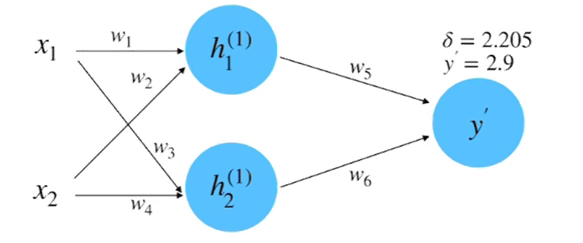
$\begin{aligned} y^{\prime}& =w_5\cdot h_1^{(1)}+w_6\cdot h_2^{(1)} \\ &=1.0\cdot1.0+2.0\cdot0.95 \\ &=2.9 \end{aligned}$
(3) 计算损失: 根据数据真实值 y=0.8 和平方差损失函数来计算损失, 如下图所示。

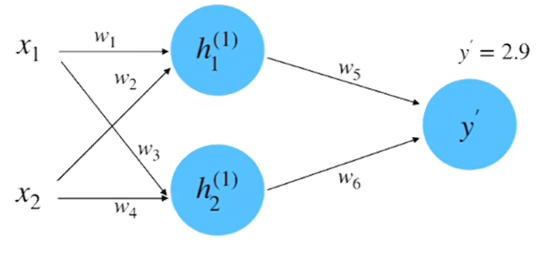
$\begin{aligned} &\delta=\frac12(y-y^{\prime})^2 \\ &=0.5(0.8-2.9)^2 \\ &=2.205 \end{aligned}$
(4) 计算梯度: 此过程实际上就是计算偏微分的过程, 以参数 $w_5$ 的偏微分计算为例,如下图所示。

根据链式法则:

$\frac{\partial\delta}{\partial w_5}=\frac{\partial\delta}{\partial y^{\prime}}\cdot\frac{\partial y^{\prime}}{\partial w_5}$

其中:

$\begin{aligned} \frac{\partial\delta}{\partial y^{\prime}}& =2\cdot\frac12\cdot\left(y-y^{\prime}\right)(-1) \\ &=y^{\prime}-y \\ &=2.9-0.8 \\ &=2.1 \end{aligned}$

$\begin{gathered} y'=w_5\cdot h_1^{(1)}+w_6\cdot h_2^{(1)} \\ \frac{\partial y^{\prime}}{\partial w_5}=h_1^{(1)}+0 \\ =1.0 \end{gathered}$

所以:

$\frac{\partial\delta}{\partial w_5}=\frac{\partial\delta}{\partial y^{\prime}}\cdot\frac{\partial y^{\prime}}{\partial w_5}=2.1\times1.0=2.1$

(5) 反向传播计算梯度: 在第 4 步中是以参数 $w_5$ 为例子来计算偏微分的。如果以参数 $w_1$ 为例子, 它的偏微分计算就需要用到链式法则, 过程如下图所示。

$\frac{\partial\delta}{\partial w_1}=\frac{\partial\delta}{\partial y^{\prime}}\cdot\frac{\partial y^{\prime}}{\partial h_1^{(1)}}\cdot\frac{\partial h_1^{(1)}}{\partial w_1}$

$\begin{gathered} y'=w_5\cdot h_1^{(1)}+w_6\cdot h_2^{(1)} \\ \frac{\partial y^{\prime}}{\partial h_1^{(1)}}=w_5+0 \\ =1.0 \end{gathered}$

$\begin{aligned}h_1^{(1)}&=w_1\cdot x_1+w_2\cdot x_2\\\frac{\partial h_1^{(1)}}{\partial w_1}&=x_1+0\\&=0.5\end{aligned}$

$\frac{\partial\delta}{\partial w_1}=\frac{\partial\delta}{\partial y^{\prime}}\cdot\frac{\partial y^{\prime}}{\partial h_1^{(1)}}\cdot\frac{\partial h_1^{(1)}}{\partial w_1}=2.1\times1.0\times0.5=1.05$

（6）梯度下降更新网络参数
假设这里的超参数 “学习速率” 的初始值为 0.1 , 根据梯度下降的更新公式, w1 参数的更新计算如下所示:

$w_1^{(\mathrm{update})}=w_1-\eta\cdot\frac{\partial\delta}{\partial w_1}=1.0-0.1\times1.05=0.895$

同理, 可以计算得到其他的更新后的参数: $w_1=0.895,w_2=0.895,w_3=0.29,w_4=0.28,w_5=0.79,w_6=1.8005$

到此为止, 我们就完成了参数迭代的全部过程。可以计算一下损失看看是否有减小, 计算如下: $\begin{aligned} &\text{} \delta=\frac12(y-y^{\prime})^2 \\ &=0.5(0.8-1.3478)^2 \\ &=0.15 \end{aligned}$

此结果相比较于之间计算的前向传播的结果 2.205, 是有明显的减小的。

极光喵

关注

33
点赞
踩
31

收藏

觉得还不错? 一键收藏
0
评论
反向传播算法（Back Propagation)

梯度下降算法的核心思想是计算损失函数对权重的偏导数，然后按照这个偏导数的反方向调整权重。反向传播是一种有效的计算梯度的方法，它可以快速计算网络中每个神经元的偏导数。反向传播通过先正向传播计算网络的输出，然后从输出层到输入层反向传播误差，最后根据误差计算每个神经元的偏导数。综上所述，梯度下降和反向传播是神经网络训练过程中两个重要的概念，梯度下降算法用于优化网络的权重，反向传播算法用于计算每个神经元的偏导数。此结果相比较于之间计算的前向传播的结果 2.205, 是有明显的减小的。的偏微分计算为例,如下图所示。
复制链接

扫一扫