一、引言
1.1 背景
机器学习
从人工智能发展而来
是为计算机开发的一种新功能
应用
数据挖掘
无法手动编写的程序(手写识别)
私人定制程序(Amazon推荐)
理解人类的学习过程和大脑
1.2 什么是机器学习
Arthur Samuel:在没有明确设置情况下,使机器具有学习能力的研究领域。
Tom Mitchell:从经验E,解决任务T,进行性能度量P,通过P测定在T上的表现因E而提高。
监督学习:教会计算机做
无监督学习:计算机自己做
1.3 监督学习
给一个数据集,其中包含了正确答案。
回归:输出连续值
分类:输出离散值
1.4 无监督学习
给一个数据集,其中没有正确答案。
聚类、鸡尾酒会算法(声音提取)
二、单变量线性回归
2.1 模型描述
m m m 代表训练集中实例的数量
x x x 代表特征/输入变量
y y y 代表目标变量/输出变量
( x , y ) \left( x,y \right) (x,y) 代表训练集中的实例
( x ( i ) , y ( i ) ) ({{x}^{(i)}},{{y}^{(i)}}) (x(i),y(i)) 代表第 i i i 个观察实例
h h h 代表学习算法的解决方案或函数也称为假设(hypothesis)
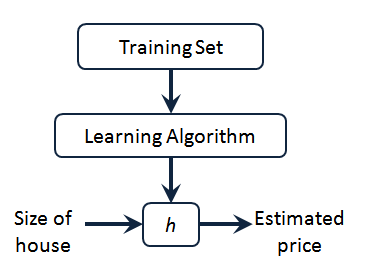
一种可能的表达方式为: h θ ( x ) = θ 0 + θ 1 x h_\theta \left( x \right)=\theta_{0} + \theta_{1}x hθ(x)=θ0+θ1x,因为只含有一个特征/输入变量,因此这样的问题叫作单变量线性回归问题。
2.2 代价函数
线性函数形式: h θ ( x ) = θ 0 + θ 1 x h_\theta \left( x \right)=\theta_{0}+\theta_{1}x hθ(x)=θ0+θ1x
为我们的模型选择合适的参数(parameters) θ 0 \theta_{0} θ0 和 θ 1 \theta_{1} θ1
我们的目标便是选择出可以使得代价函数 J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J \left( \theta_0, \theta_1 \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2} J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2最小。
我们之所以要求出误差的平方和,是因为误差平方代价函数,对于大多数问题,特别是回归问题,都是一个合理的选择。还有其他的代价函数也能很好地发挥作用,但是平方误差代价函数可能是解决回归问题最常用的手段了。
2.3 代价函数的直观理解(一)

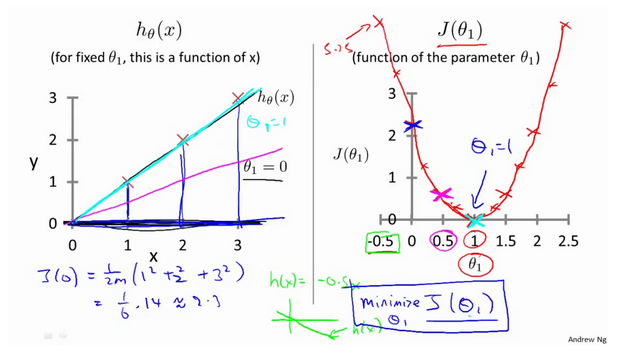
2.4 代价函数的直观理解(二)
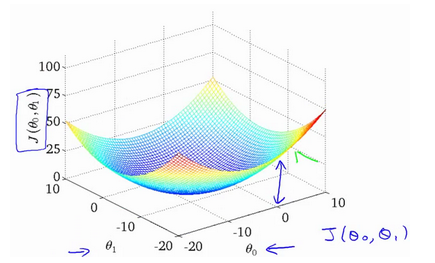
代价函数的样子,等高线图,则可以看出在三维空间中存在一个使得 J ( θ 0 , θ 1 ) J(\theta_{0}, \theta_{1}) J(θ0,θ1)最小的点。
2.5 梯度下降
梯度下降是一个用来求函数最小值的算法,我们将使用梯度下降算法来求出代价函数 J ( θ 0 , θ 1 ) J(\theta_{0}, \theta_{1}) J(θ0,θ1) 的最小值。
梯度下降背后的思想是:开始时我们随机选择一个参数的组合 ( θ 0 , θ 1 , . . . . . . , θ n ) \left( {\theta_{0}},{\theta_{1}},......,{\theta_{n}} \right) (θ0,θ1,......,θn),计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。
批量梯度下降
批量梯度下降(batch gradient descent):
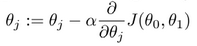
a a a是学习率(learning rate),决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。
同步更新
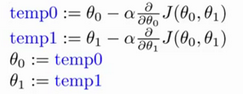
2.6 梯度下降直观理解
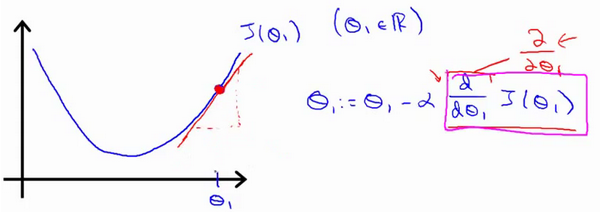
对于这个问题,求导的目的,基本上可以说取这个红点的切线斜率,现在,这条线有一个正斜率,也就是说它有正导数,因此,我得到的新的 θ 1 {\theta_{1}} θ1, θ 1 {\theta_{1}} θ1更新后等于 θ 1 {\theta_{1}} θ1减去一个正数乘以 a a a。
a a a太小,每次一小步,收敛太慢
a a a太大,每次一大步,可能无法收敛
如果初始就在局部最低点,导数是0,不会改变
2.7 线性回归的梯度下降
梯度下降算法与线性回归算法;

对之前的线性回归问题运用梯度下降,关键在于求出代价函数的导数:
∂ ∂ θ j J ( θ 0 , θ 1 ) = ∂ ∂ θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{\partial }{\partial {{\theta }_{j}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{\partial }{\partial {{\theta }_{j}}}\frac{1}{2m}{{\sum\limits_{i=1}^{m}{\left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)}}^{2}} ∂θj∂J(θ0,θ1)=∂θj∂2m1i=1∑m(hθ(x(i))−y(i))2
j = 0 j=0 j=0 时: ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \frac{\partial }{\partial {{\theta }_{0}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{1}{m}{{\sum\limits_{i=1}^{m}{\left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)}}} ∂θ0∂J(θ0,θ1)=m1i=1∑m(hθ(x(i))−y(i))
j = 1 j=1 j=1 时: ∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) ) \frac{\partial }{\partial {{\theta }_{1}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{1}{m}\sum\limits_{i=1}^{m}{\left( \left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)\cdot {{x}^{(i)}} \right)} ∂θ1∂J(θ0,θ1)=m1i=1∑m((hθ(x(i))−y(i))⋅x(i))
则算法变成了
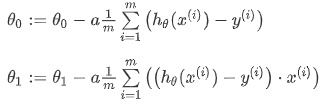
批量梯度下降
指的是在梯度下降的每一步中,都用到了所有的(一批)训练样本。
三、线性代数回顾(Linear Algebra Review)
已掌握内容,跳过。
四、多变量线性回归(Linear Regression with Multiple Variables)
4.1 多维特征

h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θ0+θ1x1+θ2x2+...+θnxn
特征矩阵 X X X的维度是 m ∗ ( n + 1 ) m*(n+1) m∗(n+1)。 因此公式可以简化为: h θ ( x ) = θ T X h_{\theta} \left( x \right)={\theta^{T}}X hθ(x)=θTX,其中上标 T T T代表矩阵转置。
4.2 多变量梯度下降
J ( θ 0 , θ 1 . . . θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( {\theta_{0}},{\theta_{1}}...{\theta_{n}} \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( h_{\theta} \left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}} J(θ0,θ1...θn)=2m1i=1∑m(hθ(x(i))−y(i))2
其中, h θ ( x ) = θ T X = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_{\theta}\left( x \right)=\theta^{T}X={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θTX=θ0+θ1x1+θ2x2+...+θnxn
目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数
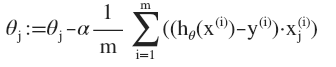
4.3 梯度下降实践-特征缩放
面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间。
最简单的方法是令: x n = x n − μ n s n {{x}_{n}}=\frac{{{x}_{n}}-{{\mu}_{n}}}{{{s}_{n}}} xn=snxn−μn,其中 μ n {\mu_{n}} μn是平均值, s n {s_{n}} sn是标准差。
4.4 梯度下降实践-学习率
每次迭代受到学习率的影响
如果过小,则达到收敛所需的迭代次数会非常高;
如果 a a a过大,每次迭代可能越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率:
α = 0.01 , 0.03 , 0.1 , 0.3 , 1 , 3 , 10 \alpha=0.01,0.03,0.1,0.3,1,3,10 α=0.01,0.03,0.1,0.3,1,3,10
4.5 特征和多项式回归
线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如一个二次方模型:
h
θ
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
2
h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}
hθ(x)=θ0+θ1x1+θ2x22
或者三次方模型:
h
θ
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
2
+
θ
3
x
3
3
h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}+{\theta_{3}}{x_{3}^3}
hθ(x)=θ0+θ1x1+θ2x22+θ3x33,通常我们需要先观察数据然后再决定准备尝试怎样的模型。另外,我们可以令:
x 2 = x 2 2 , x 3 = x 3 3 {{x}_{2}}=x_{2}^{2},{{x}_{3}}=x_{3}^{3} x2=x22,x3=x33,从而将模型转化为线性回归模型。
4.6 正规方程
到目前为止,我们都在使用梯度下降算法,但是对于某些线性回归问题,正规方程方法是更好的解决方案。
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的: ∂ ∂ θ j J ( θ j ) = 0 \frac{\partial}{\partial{\theta_{j}}}J\left( {\theta_{j}} \right)=0 ∂θj∂J(θj)=0 。
比如:
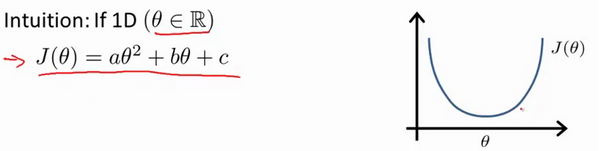
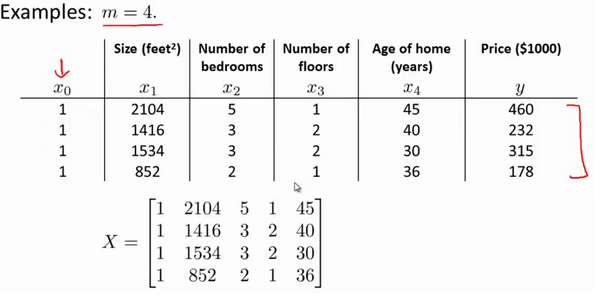
由公式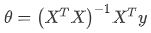 ,得:
,得: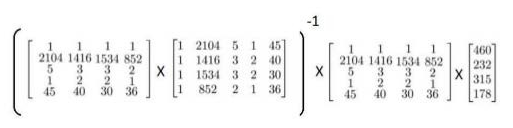
梯度下降和正规方程比较:
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 α \alpha α | 不需要 |
| 需要多次迭代 | 一次运算得出 |
| 当特征数量 n n n大时也能较好适用 | 需要计算 ( X T X ) − 1 {{\left( {{X}^{T}}X \right)}^{-1}} (XTX)−1 如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为 O ( n 3 ) O\left( {{n}^{3}} \right) O(n3),通常来说当 n n n小于10000 时还是可以接受的 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
4.7 正规方程及不可逆性
当特征值过多,即m≤n的时候,会出现矩阵不可逆的情况。
使用一种叫做正则化的线性代数方法,通过删除某些特征或者是使用某些技术,来解决当 m m m比 n n n小的时候的问题。
五、Octave教程(Octave Tutorial)
无关内容,暂时跳过。
六、逻辑回归(Logistic Regression)
6.1 分类问题
预测的变量y是离散的值
如果使用线性回归,即使所有的训练样本的标签y都等于0或1,输出值也可能远大于1,或远小于0。
使用逻辑回归算法,使输出值永远在0-1之间。
6.2 假说表示
引入新模型——逻辑回归,该模型的输出值永远在0-1之间。
逻辑回归的模型的假设是: h θ ( x ) = g ( θ T X ) h_\theta \left( x \right)=g\left(\theta^{T}X \right) hθ(x)=g(θTX)
其中, X X X 代表特征向量, g g g 代表逻辑函数(logistic function),一个常用的逻辑函数为S形函数(Sigmoid function),公式为: g ( z ) = 1 1 + e − z g\left( z \right)=\frac{1}{1+{{e}^{-z}}} g(z)=1+e−z1。
h θ ( x ) h_\theta \left( x \right) hθ(x)的作用是,对于给定的输入变量,根据选择的参数计算输出变量=1的可能性即 h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\theta \left( x \right)=P\left( y=1|x;\theta \right) hθ(x)=P(y=1∣x;θ)
6.3 判定边界
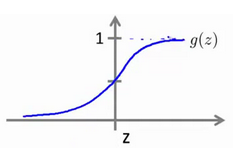
当 h θ ( x ) > = 0.5 {h_\theta}\left( x \right)>=0.5 hθ(x)>=0.5时,预测 y = 1 y=1 y=1。
当 h θ ( x ) < 0.5 {h_\theta}\left( x \right)<0.5 hθ(x)<0.5时,预测 y = 0 y=0 y=0 。
根据图像,我们知道:
z = 0 z=0 z=0 时 g ( z ) = 0.5 g(z)=0.5 g(z)=0.5
z > 0 z>0 z>0 时 g ( z ) > 0.5 g(z)>0.5 g(z)>0.5
z < 0 z<0 z<0 时 g ( z ) < 0.5 g(z)<0.5 g(z)<0.5
又因为
z
=
θ
T
x
z={\theta^{T}}x
z=θTx ,即:
θ
T
x
>
=
0
{\theta^{T}}x>=0
θTx>=0 时,预测
y
=
1
y=1
y=1
θ
T
x
<
0
{\theta^{T}}x<0
θTx<0 时,预测
y
=
0
y=0
y=0
对于模型: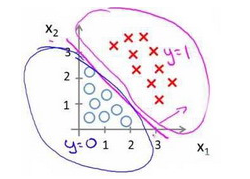
直线是模型的分界线。
对于模型: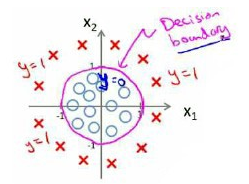 单位圆是分界线。
单位圆是分界线。
我们可以用非常复杂的模型来适应非常复杂形状的判定边界。
6.4 代价函数
在线性回归模型中,代价函数是误差的平方和。
但是,在逻辑回归模型中如果继续使用平方和,会使代价函数变成非凸函数。
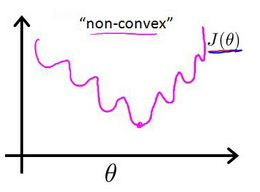
这样代价函数会有很多局部最小值,影响梯度下降寻找全局最小值。
重新定义: J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{{Cost}\left( {h_\theta}\left( {x}^{\left( i \right)} \right),{y}^{\left( i \right)} \right)} J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))
其中,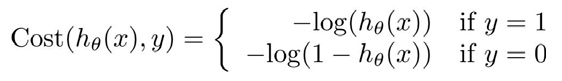
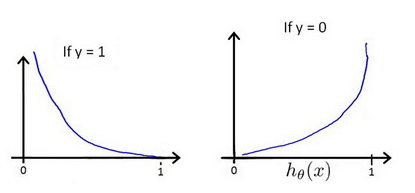
可以将
C
o
s
t
(
h
θ
(
x
)
,
y
)
Cost\left( {h_\theta}\left( x \right),y \right)
Cost(hθ(x),y)简化如下:
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
×
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
×
l
o
g
(
1
−
h
θ
(
x
)
)
Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right)
Cost(hθ(x),y)=−y×log(hθ(x))−(1−y)×log(1−hθ(x))
这样代价函数为:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]} J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
这样就可以使用梯度下降了。
θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j} J(\theta) θj:=θj−α∂θj∂J(θ)
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j := \theta_j - \alpha \frac{1}{m}\sum\limits_{i=1}^{m}{{\left( {h_\theta}\left( \mathop{x}^{\left( i \right)} \right)-\mathop{y}^{\left( i \right)} \right)}}\mathop{x}_{j}^{(i)} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
除梯度下降算法之外,还有一些令代价函数最小的算法。不需要人工选择学习率,更加迅速。
共轭梯度(Conjugate Gradient),局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS)
6.5 简化的成本函数和梯度下降
上一节得到的代价函数: J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]} J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
找到 min θ J ( θ ) \underset{\theta}{\min }J\left( \theta \right) θminJ(θ) ,也是使用 θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) {\theta_j}:={\theta_j}-\alpha \frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}}){{x}_{j}}^{(i)}} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i),和线性回归是相同的式子。但是,他们的算法不同,因为假设函数是不一样的。
另外,逻辑回归是可以使用for循环来做的。理想情况下,我么更提倡向量化实现。
逻辑回归同样可以使用特征缩放。
6.6 高级优化
三种算法:共轭梯度法 BFGS (变尺度法) 和L-BFGS (限制变尺度法)
使用这种算法,不需要手动选择学习率 α \alpha α,算法有一个智能的内部循环,称为线性搜索算法,会自动尝试并选择好的学习率。
但是实现复杂,需要使用软件库。
6.7 多类别分类:一对多
二分类与多分类:
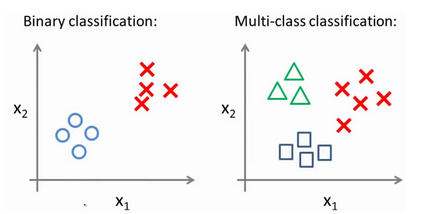
方法:将多个类中的一个类标记为正向类( y = 1 y=1 y=1),然后将其他所有类都标记为负向类,这个模型记作 h θ ( 1 ) ( x ) h_\theta^{\left( 1 \right)}\left( x \right) hθ(1)(x)。接着,类似地第我们选择另一个类标记为正向类( y = 2 y=2 y=2),再将其它类都标记为负向类,将这个模型记作 h θ ( 2 ) ( x ) h_\theta^{\left( 2 \right)}\left( x \right) hθ(2)(x),依此类推。
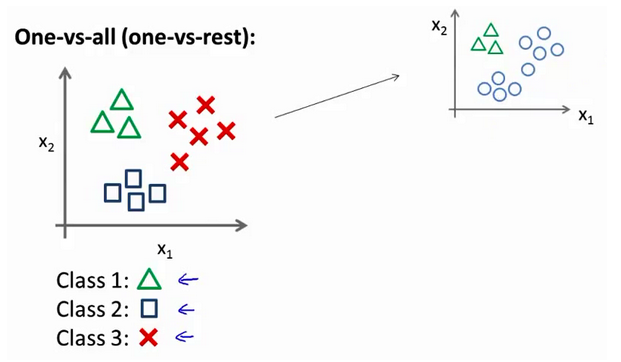
在三个分类器里面输入 x x x,然后我们选择一个让 h θ ( i ) ( x ) h_\theta^{\left( i \right)}\left( x \right) hθ(i)(x) 最大的$ i , 即 ,即 ,即\mathop{\max}\limits_i,h_\theta^{\left( i \right)}\left( x \right)$。
七、正则化
7.1 过拟合的问题
回归问题:
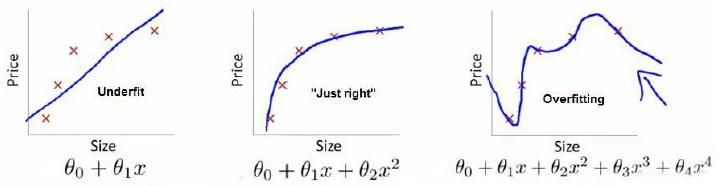
第一个模型是一个线性模型,欠拟合;第三个模型是一个四次方的模型,过于强调拟合原始数据,若给出一个新的值使之预测,它将表现的很差,是过拟合;而中间的模型似乎最合适。
分类问题:
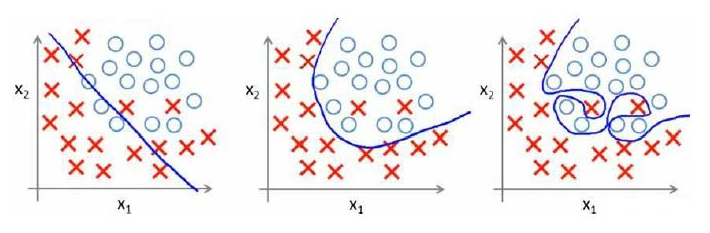
以多项式理解, x x x 的次数越高,拟合的越好,但相应的预测的能力就可能变差。
发现过拟合如何处理:
- 丢弃不能帮我们正确预测的特征。可以手工选择或者使用模型选择算法来帮忙。
- 正则化。保留所有特征,减少参数大小。
7.2 代价函数
根据上一节,正式高次项导致了过拟合的产生,所以要通过让高次项的系数接近于0,来进行拟合。
我们决定要减少 θ 3 {\theta_{3}} θ3和 θ 4 {\theta_{4}} θ4的大小,我们要做的便是修改代价函数,在其中 θ 3 {\theta_{3}} θ3和 θ 4 {\theta_{4}} θ4 设置一点惩罚。
修改后的代价函数如下: min θ 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + 1000 θ 3 2 + 10000 θ 4 2 ] \underset{\theta }{\mathop{\min }}\,\frac{1}{2m}[\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}+1000\theta _{3}^{2}+10000\theta _{4}^{2}]} θmin2m1[i=1∑m(hθ(x(i))−y(i))2+1000θ32+10000θ42]
假设我们有很多参数,不知道要惩罚哪一些,我们便对所有特征进行惩罚。
J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J\left( \theta \right)=\frac{1}{2m}[\sum\limits_{i=1}^{m}{{{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}+\lambda \sum\limits_{j=1}^{n}{\theta_{j}^{2}}]} J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
其中,$\lambda $称为正则化参数。
7.3 正则化线性回归
梯度下降
θ 0 : = θ 0 − a 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) ) {\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{0}^{(i)}}) θ0:=θ0−am1i=1∑m((hθ(x(i))−y(i))x0(i)) θ j : = θ j − a [ 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] {\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{j}^{\left( i \right)}}+\frac{\lambda }{m}{\theta_j}] θj:=θj−a[m1i=1∑m((hθ(x(i))−y(i))xj(i)+mλθj] , f o r for for j = 1 , 2 , . . . n j=1,2,...n j=1,2,...n
对于$ j=1,2,…,n$ 时的更新式子进行调整可得:
θ
j
:
=
θ
j
(
1
−
a
λ
m
)
−
a
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
{\theta_j}:={\theta_j}(1-a\frac{\lambda }{m})-a\frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{j}^{\left( i \right)}}
θj:=θj(1−amλ)−am1i=1∑m(hθ(x(i))−y(i))xj(i)
可以看出,正则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令$\theta $值减少了一个额外的值。
正规方程
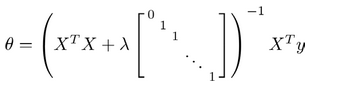
7.4 正则化的逻辑回归模型
梯度下降
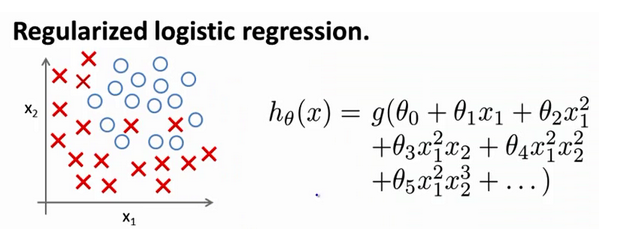
同样给代价函数增加一个正则化的表达式,得到代价函数:
J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}+\frac{\lambda }{2m}\sum\limits_{j=1}^{n}{\theta _{j}^{2}} J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
求导之后,同线性回归表达式相同:
θ 0 : = θ 0 − a 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) ) {\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{0}^{(i)}}) θ0:=θ0−am1i=1∑m((hθ(x(i))−y(i))x0(i))
θ j : = θ j − a [ 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] {\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{j}^{\left( i \right)}}+\frac{\lambda }{m}{\theta_j}] θj:=θj−a[m1i=1∑m((hθ(x(i))−y(i))xj(i)+mλθj] , f o r for for j = 1 , 2 , . . . n j=1,2,...n j=1,2,...n
注意:
-
虽然正则化的逻辑回归中的梯度下降和正则化的线性回归中的表达式看起来一样,但由于两者的 h θ ( x ) {h_\theta}\left( x \right) hθ(x)不同所以还是有很大差别。
-
θ 0 {\theta_{0}} θ0不参与其中的任何一个正则化。






















 1791
1791











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








