buck电源环路建模、测量和优化(二)

        接上一节的内容，本节笔记记录的问题：

1、为什么需要设计环路补偿？

2、3种补偿拓扑电路、零极点计算、电路参数确定。

• 为什么要设计环路补偿

        当电源的输入输出等基本参数确定下来，如果需要调整电源的动态性能，那么调节环路补偿时最为简单的。电源在工作中可能遇到不同的输入和负载的变化，我们需要关心的是，无论负载和输入如何变化，电源都不会出现不稳定的情况。从直流到高频段，电源所表现出来的增益和相位有所不同，而在某些频率段，电源输出可能不在稳定。由第一节的闭环系统框图可知：

        一个闭环系统需要稳定，需要满足分母不能为0，因为分母为0就代表这个系统增益无穷大，现实中不存在这种情况。那什么情况下分母为0呢？即幅值为1，且相位为-180。在系统设计时，设计人员要尽可能避免出现这种情况，并且设计指标尽量远离这两个指标，这也就时为什么我们要强调预留一定的增益裕量和相位裕度。

        总言之，环路补偿环节，是为了让电源在所有工况下都不会出现不稳定的情况。

• 理想电源的开环传递函数幅频特性：

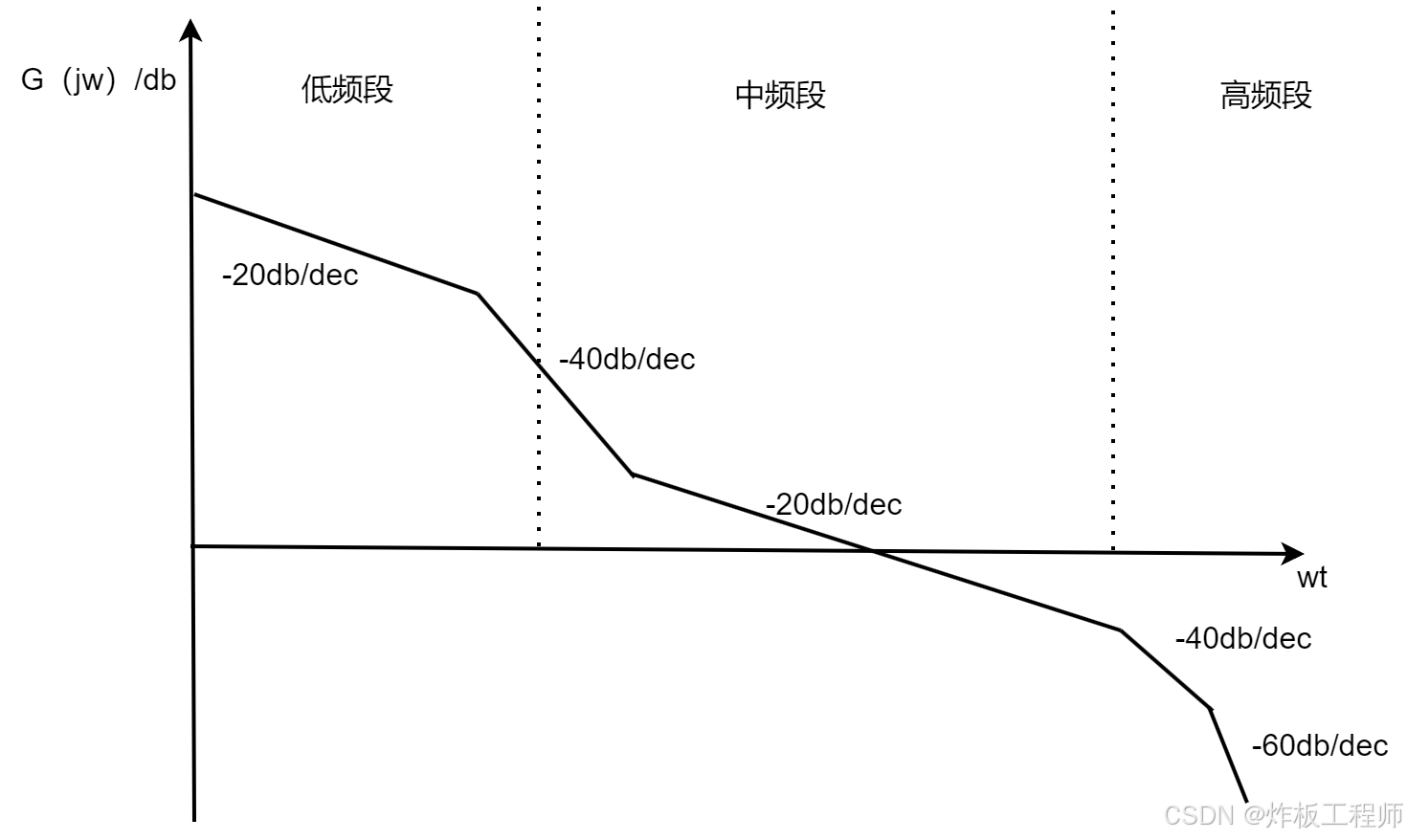
        在低频段，开环传递函数反映了系统包含积分环节的个数和直流增益的大小，它主要影响系统的稳态性能。

        在中频段，大致是以-20db/dec的斜率下降并穿越0db线。中频段的宽度与系统的动态稳定性密切相关，宽度越大，相位裕量越大；穿越频率越高，系统的响应越快但超调量也越高。对于开关系统，过高的穿越频率可能导致开关频率及其谐波、寄生振荡引起额高频分量无法有效抑制，引起系统的不稳定。因此理想的中频特性中，可以增加一个极点，使得曲线以-40db/dec的斜率下降，然后在中频段的合适位置再通过一个零点提升增益。这两个点的频段不能太大，否则会引起较大的相位滞后，影响系统的稳定性。

        在高频段，此时频率已经远离穿越频率点，对系统的动态性能影响不大，主要反映系统对高频干扰的抑制能力。我们希望高频段衰减越快越好。

• LC滤波器的ESR零点

        假设电容的ESR不存在，，可见双极点位于处。

当电容存在ESR时，

        通常ESR的值比较小，对于极点的影响可以忽略不记。但是ESR的存在会在处增加一个零点，这会导致增益的增加。特别是在高频段，增益的增加会增加高频噪声干扰的机会，还可能导致稳定性的问题，这点是需要注意的。

• 三种补偿拓扑

 I型补偿：

        I型补偿是最简单的。电容C1引入了一个极点，其频率在处，极点的存在使得增益曲线-20db/dec。这种补偿方式会使得整个系统的增益下降，电源的截止频率变低，对于任何输入或负载的变化都变得缓慢，因此在很多电路中都不适用。但在一些特殊情况下就很合适，例如全新的样机第一次上电，需要人为迫使其无条件稳定，这样可以评估和优化预期设计的所有静态特性。

II型补偿：

        II型补偿在低频段和I型补偿一样，在频率0处存在一个极点，增益由R1与C1决定。随后R2与C2构成一个零点，使得增益增加。这里通常会把这个零点设置在LC滤波器的极点频率处以抵消双极点带来的增益降低。而R1、R2的取值决定了中间水平段曲线的增益。最后，R2与C1引入一个极点，会设置在LC滤波器的ESR零点频率处，用于抵消ESR零点的影响。

        II型补偿并不能满足大多数电压控制型的系统。在具有正增益的情况下，初始极点和LC滤波器的剩余极点总相位将达到180度，会导致系统不稳定。然而II型补偿非常适合电流控制模式的电路，因为在电流控制模式下输出滤波器的截止频率以内只有一个极点，同样，在DCM模式下，由于系统是一阶的，II型补偿也很适用。

        III型补偿：

        III型补偿具2两个零点和3个极点。首先第一个极点位于频率处，和I型补偿一样。然后我们在LC滤波器的双极点频率处，设置两个零点，用于提高增益和相位。这两个零点分别由R1，C3和R2,C2确定。再然后，在LC滤波器的ESR零点频率处设置一个极点，用来消除ESR带来的增益增加。最后，通常在开关频率或者更高频率处设置最后一个极点，使得在高频段增益下降，总增益小于1，满足稳定性的要求。

        III型补偿虽然比较复杂，但适应性非常好，能够满足大部分电源应用。如何设计一个III型补偿电路？这里有一个设计实例非常值得参考。

        电源规格：

Vin=3.3V（3.6V max）

Vout=1.2V

最大负载电流=10A

开关频率：f=600kHz

Vref=700mV

PWM斜坡电压Vp=1.0V

电感L=0.68uH

输出电容C=470uF

电容ESR（max）=10 mohm

误差放大器的增益带宽积GBW=5MHz

由上一节可知，PWM级的增益为输入电压与斜坡电压的比值：

然后计算LC滤波器的双极点位置：

在这里还要考虑电容的ESR引入的零点。电容的ESR具有负温度系数，设计时还需要考虑其最低温度的情况：

        由于我们希望开关电源能够对快速变化的负载有较好的动态响应，这里需要很宽的带宽，所以宜采用III型补偿电路。根据采样定理，采样频率为信号频率的2倍才能不失真还原信号，而如果要提供线性控制，则需要在一个开关周期里采样5次。这就意味着控制环路的截止频率不应高于开关频率的20%。在这个例子里，截止频率设置为100kHz是一个合理的值。

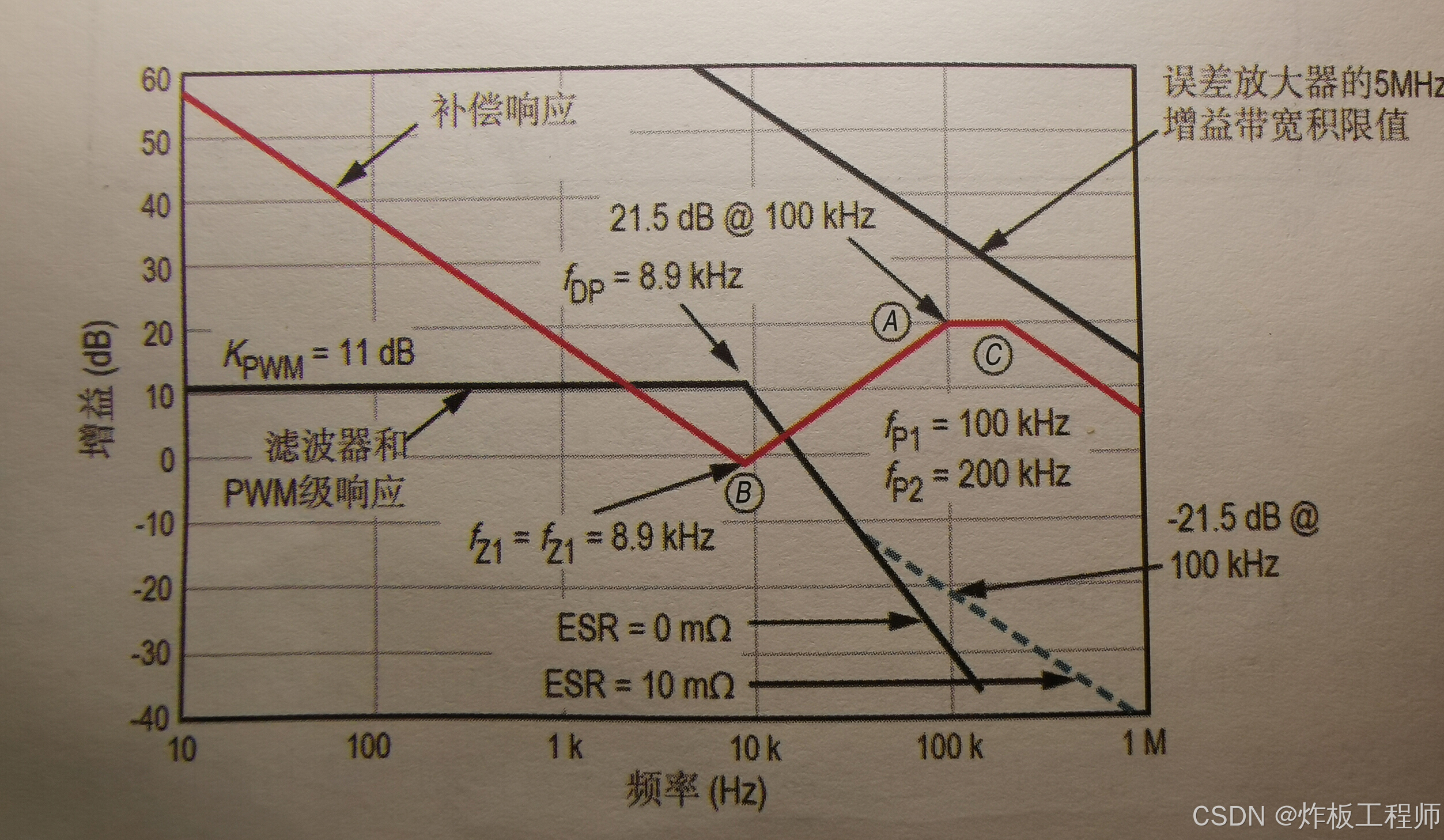
        应当注意到，传递函数里的不同环节的增益相乘，反应到波特图上就是不同增益曲线值的相加。在f=8.9kHz处放置两个零点，用于补偿滤波器的增益下降，补偿网络的增益将从-20db/dec变为+20db/dec。在100kHz频率处设置一个极点，设置f=100kHz处，增益为+21.5db，这样与滤波器增益的-21.5db相加刚好使得环路增益为0，即为截止频率点。

        到这里，我们的III型补偿还有一个极点需要设置。由于运放增益带宽积的限制，最后一个极点的频率不能设置太高，在这里可以设为200kHz。最后需要注意的是，这里ESR按照最大值10m ohm计算，而随着ESR越来越小，截止频率点将从100kHz降低接近40kHz。

        那么接下来就是最后一步——确定电路的参数。电路存在2个零点和3个极点，其中一个极点位于f=0处，其余4个可以由下式子确定。

        这几个式子怎么来的呢？需要列出补偿网络的传递函数，然后分别令分子为零，得到零点；令分母为零，得到极点。以上式子仅仅是零极点的近似值（为了计算方便）。

        我们看到，有些RC器件是相互耦合的，一个元件既影响零点，也会影响极点。由于R-C支路在更高的频率下起作用，就意味着R1>>R3，C2>>C1。

        这里R4为分压电阻，无论R4取何值，根据虚短可知其上端电压都为Vref。它在电路中并不影响补偿网络的增益和相位，可以先确定这个参数，这里选定为10K。

        那么：

        知道了R1，就可以算出C3: 

        得到C3后，又可以确定R3: 

        现在知道增益补偿的目标是在环路截止频率处，补偿电路的增益为21.5db或者说是12V/V。而这个增益是由R2和R1//R3的比例决定的。（增益需要从传递函数中得到，将传递函数化为尾1标准型）： 

        知道R2后，可以求出C2:

        最后再计算C1的值：

        到这里，整个环路补偿电路就设计完成了。

        

参考：

《电源设计基础》第6章 6.5、6.6节

《开关变换器的建模与控制》第4章4.2节