基于最小二乘法的磁力计椭球拟合方法

最新推荐文章于 2024-01-25 11:44:37 发布

Aromash

最新推荐文章于 2024-01-25 11:44:37 发布

阅读量1.1w

点赞数 6

分类专栏：飞控算法文章标签：最小二乘估计磁力计校正椭球拟合

本文链接：https://blog.csdn.net/qq_39554681/article/details/89527267

版权

飞控算法专栏收录该内容

11 篇文章 25 订阅

订阅专栏

基于最小二乘法的磁力计椭球拟合方法

在写飞控代码时，必然要对磁力计的测量数据进行校正，本文将介绍一种简单实用的校正方法–基于最小二乘法的椭球拟合方法。

本文椭球拟合部分来自博文IMU加速度、磁力计校正－－椭球拟合，本文对最小二乘估计进行了部分推导，最后使用实测的数据完成了磁力计的椭球拟合。

椭球拟合

磁力计在测量磁场强度时，在环境不变的情况下，传感器每个姿态感受磁场强度是相同的，磁力计测量的x,y,z轴值，在没有偏差且传感器内部x,y,z轴相互垂直的情况下，在三维空间中组成一个圆球面。但是磁力计存在Hard Iron Distortion和Soft Iron Distortion。使得x,y,z轴度量单位不相同，各轴也并非相互垂直，(说明一下，任意椭球的三个轴都是相互垂直的，几何上，椭球最长的轴与最短的轴相互垂直，从代数的角度看，对称正定矩阵 $A=R^{\prime} B R$ ，其中 $B$ 为对角线大于0表示各轴长度的对角矩阵， $R$ 为旋转矩阵， $R^{\prime} R=I$ ，所以磁通量的空间坐标虽然形成一个椭球，椭球各轴相互垂直，但这个垂直的轴已经不是传感器 $x, y, z$ 轴了)椭球球心也并非[0,0,0]，坐标磁通量在三维空间组成的椭球球心，是磁力计的校准值的一部分。

数学模型:

我们让磁力计尽可能多地采集到空间各个方向上的磁场强度，最后的测量数据将会形成空间上的一个椭圆，而校正问题在于给定椭球球面上的点，如何求椭球球心。其实就是一个椭球拟合问题。

$a_{1} x^{2}+a_{2} y^{2}+a_{3} z^{2}+a_{4} x y+a_{5} x z+a_{6} y z+a_{7} x+a_{8}y+a_{9} z=1$

从几何的角度表示上式的椭球为：
$\left[ \begin{array}{ccc}{x-c_{x}} & {y-c_{y}} & {z-c_{z}}\end{array}\right] \left[ \begin{array}{ccc}{r_{11}} & {r_{12}} & {r_{13}} \\ {r_{21}} & {r_{22}} & {r_{23}} \\ {r_{31}} & {r_{32}} & {r_{33}}\end{array}\right]^{T} \left[ \begin{array}{ccc}{\lambda_{1}} & {0} & {0} \\ {0} & {\lambda_{2}} & {0} \\ {0} & {0} & {\lambda_{3}}\end{array}\right] \left[ \begin{array}{ccc}{r_{11}} & {r_{12}} & {r_{13}} \\ {r_{21}} & {r_{22}} & {r_{23}} \\ {r_{31}} & {r_{32}} & {r_{33}}\end{array}\right] \left[ \begin{array}{c}{x-c_{x}} \\ {y-c_{y}} \\ {z-c_{z}}\end{array}\right]$
$=1+\left[ \begin{array}{lll}{c_{x}} & {c_{y}} & {c_{z}}\end{array}\right] \left[ \begin{array}{ccc}{r_{11}} & {r_{12}} & {r_{13}} \\ {r_{21}} & {r_{22}} & {r_{23}} \\ {r_{31}} & {r_{32}} & {r_{33}}\end{array}\right]^{T} \left[ \begin{array}{ccc}{\lambda_{1}} & {0} & {0} \\ {0} & {\lambda_{2}} & {0} \\ {0} & {0} & {\lambda_{3}}\end{array}\right] \left[ \begin{array}{ccc}{r_{11}} & {r_{12}} & {r_{13}} \\ {r_{21}} & {r_{22}} & {r_{23}} \\ {r_{31}} & {r_{32}} & {r_{33}}\end{array}\right] \left[ \begin{array}{c}{c_{x}} \\ {c_{y}} \\ {c_{z}}\end{array}\right]$
写成矩阵形式：
$X-C] M[X-C]^{T}=1+C M C^{T}$
$X M X^{T}-2 C M X^{T}+C M C^{T}=1+C M C^{T}$
其中 $X=\left[ \begin{array}{lll}{x} & {y} & {z}\end{array}\right]$ 表示椭球上的点， $C=\left[ \begin{array}{lll}{c_{x}} & {c_{y}} & {c_{z}}\end{array}\right]$ 表示椭球的球心；

$M=R^{T} B R=\left[ \begin{array}{ccc}{r_{11}} & {r_{12}} & {r_{13}} \\ {r_{21}} & {r_{22}} & {r_{23}} \\ {r_{31}} & {r_{32}} & {r_{33}}\end{array}\right]^{T} \left[ \begin{array}{ccc}{\lambda_{1}} & {0} & {0} \\ {0} & {\lambda_{2}} & {0} \\ {0} & {0} & {\lambda_{3}}\end{array}\right] \left[ \begin{array}{ccc}{r_{11}} & {r_{12}} & {r_{13}} \\ {r_{21}} & {r_{22}} & {r_{23}} \\ {r_{31}} & {r_{32}} & {r_{33}}\end{array}\right]=\left[ \begin{array}{ccc}{a_{1}} & {a_{4} / 2} & {a_{5} / 2} \\ {a_{4} / 2} & {a_{2}} & {a_{6} / 2} \\ {a_{5} / 2} & {a_{6} / 2} & {a_{3}}\end{array}\right]$
可得球心的表达形式：
$C=-\frac{1}{2}\left[a_{7}, a_{8}, a_{9}\right](M)^{-1}$

其他参数：
$S S=C M C^{T}+1$

椭球 $x$ 轴长度： $x_{s c a l e}=\sqrt{\frac{S S}{\lambda_{1}}}$
椭球 $y$ 轴长度： $y_{s c a l e}=\sqrt{\frac{S S}{\lambda_{2}}}$
椭球 $z$ 轴长度： $z_{s c a l e}=\sqrt{\frac{S S}{\lambda_{3}}}$

接下来就是如何使用最小二乘法从测量数据中求出椭圆的9个参数。

最小二乘估计

下面举一个最小二乘估计的简单例子：

假设有下列 $r$ 组观测数据
$x_1,y_1),…(x_r,y_r)]$

若待估计的形式为
$y=ax^2+bx+c$

则有

$\boldsymbol{y}_{i}=\left( \begin{array}{ccc}{\boldsymbol{x}_{i}^{2}} & {\boldsymbol{x}_{i}} & {1}\end{array}\right) \left( \begin{array}{l}{\boldsymbol{a}} \\ {\boldsymbol{b}} \\ {\boldsymbol{c}}\end{array}\right)$

即

$Y = H K$

$\boldsymbol{H}=\left( \begin{array}{ccc}{\boldsymbol{x}_{1}^{2}} & {\boldsymbol{x}_{1}} & {1} \\ {\boldsymbol{x}_{2}^{2}} & {\boldsymbol{x}_{2}} & {1} \\ {\vdots} & {\vdots} & {\vdots} \\ {\boldsymbol{x}_{r}^{2}} & {\boldsymbol{x}_{r}} & {1}\end{array}\right)$

最优估计问题转换成线性方程组的求解。

当 $H$ 列满秩时(即观测量数目大于待定参数数目时)，方程有解，此时左右同时乘 $H$ 的最小二乘逆(左逆) $inv(H)=(H^T H)^{-1}H^T$

那么

$\boldsymbol{k}=\left( \begin{array}{c}{\boldsymbol{a}} \\ {\boldsymbol{b}} \\ {\boldsymbol{c}}\end{array}\right)=\left(\boldsymbol{H}^{T} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{T} \boldsymbol{Y}$

最终得到线性方程组的解，即为最小二乘解(确定的 $k$ 对所有的测量参数都适用，实际上，最小二乘解保证了误差的平方和最小，证明过程参见博文大疆笔试中的涉及矩阵最小二乘求解思路)

同样的，对磁力计椭球拟合来讲，其待估计的形式为：

$a_{1} x^{2}+a_{2} y^{2}+a_{3} z^{2}+a_{4} x y+a_{5} x z+a_{6} y z+a_{7} x+a_{8}y+a_{9} z=1$

可以写成如下形式

$1=\left( \begin{array}{llllllllll}{x^{2}} & {y^{2}} & {z^{2}} & {x y} & {x z} & {y z} & {x} & {y} & {z}\end{array}\right) \left( \begin{array}{c}{a_{1}} \\ {\vdots} \\ {a_{9}}\end{array}\right)$

我们将所有的观测数据带入可得:

$\left( \begin{array}{c}{1} \\ {1} \\ {\vdots} \\ {1}\end{array}\right)=\left( \begin{array}{ccccccc}{x_{1}^{2}} & {y_{1}^{2}} & {z_{1}^{2}} & {\cdots} & {x_{1}} & {y_{1}} & {z_{1}} \\ {x_{2}^{2}} & {y_{2}^{2}} & {z_{2}^{2}} & {\cdots} & {x_{2}} & {y_{2}} & {z_{2}} \\ {\vdots} & {\vdots} & {\vdots} & {\ddots} & {\vdots} & {\vdots} & {\vdots} \\ {x_{r}^{2}} & {y_{r}^{2}} & {z_{r}^{2}} & {\cdots} & {x_{r}} & {y_{r}} & {z_{r}}\end{array}\right) \left( \begin{array}{c}{a_{1}} \\ {a_{2}} \\ {\vdots} \\ {a_{9}}\end{array}\right)$

求上述方程的最小二乘解：

$k=\left( \begin{array}{l}{a_{1}} \\ {a_{2}} \\ {\vdots} \\ {a_{9}}\end{array}\right)=\left(H^{T} H\right)^{-1} H^{T} Y$

即可求得最优估计的椭圆参数。

matlab平台下的磁力计校正

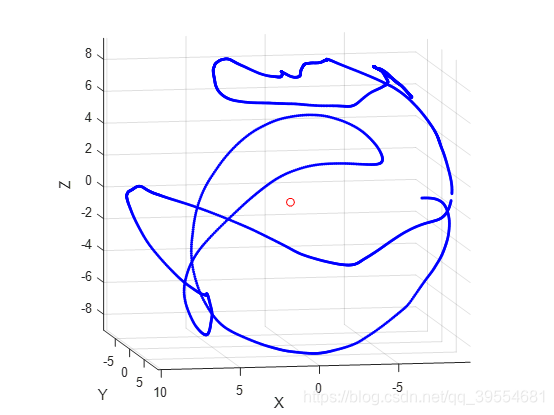
将MPU9250的磁力计测量数据通过嵌入式平台导入上位机，再在matlab平台下进行椭球拟合，值得注意的是磁力计的测量数据应当尽量遍历空间中的各个指向，这样才能得到更精确的拟合效果(图中的采样数据较少)；如效果图所示，拟合算法基本能精确计算出椭球球心位置，这表示了磁力计三轴的偏移量，而实际飞控代码中也应对磁力计初始数据减去该偏移量。
在这里插入图片描述

Aromash

关注

6
点赞
踩
96

收藏

觉得还不错? 一键收藏
17
评论
基于最小二乘法的磁力计椭球拟合方法

基于最小二乘法的磁力计椭球拟合方法在写飞控代码时，必然要对磁力计的测量数据进行校正，本文将介绍一种简单实用的校正方法–基于最小二乘法的椭球拟合方法。本文椭球拟合部分来自博文IMU加速度、磁力计校正－－椭球拟合，本文对最小二乘估计进行了部分推导，最后使用实测的数据完成了磁力计的椭球拟合。椭球拟合磁力计在测量磁场强度时，在环境不变的情况下，传感器每个姿态感受磁场强度是相同的，磁力计测量的x,y...
复制链接

扫一扫