信息论：熵、相对熵、互信息、链式法则

Entropy

熵的定义

二进制熵函数：


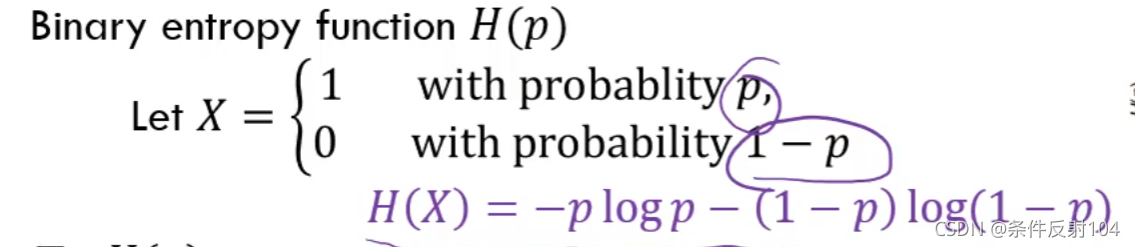
熵还可以看作是以下的期望值：

对于熵有以下性质：

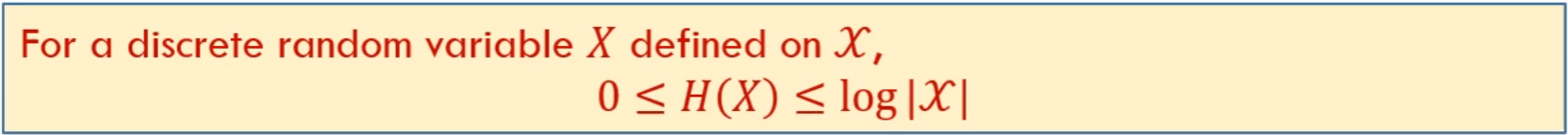
Joint Entropy

联合熵的定义：

联合熵与熵的结论：

联合熵同样可以写为期望的形式：

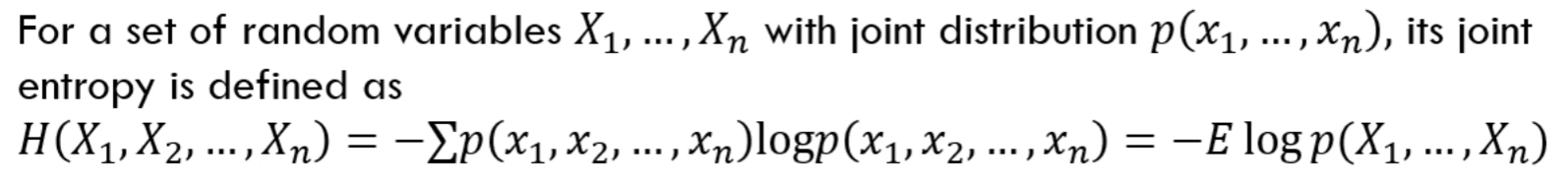
Conditional Entropy

在给定$X=x$的情况下，熵的定义为：

条件熵，是对以上X取值去顶情况下的期望：

对于各种熵有如下结论：

链式法则

与概率中的链式法则相似，因为熵是log p的期望，在概率中是乘积，则在熵中的链式法则就是相加。

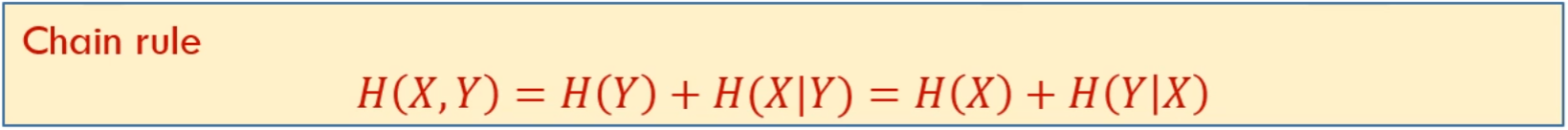
用venn图表示链式法则：

Zero Entropy

Relative Entropy

相对熵又叫做KL distance，是对两个分布之间距离的度量。

当q取值为0，此时KL distance为无穷。

相对熵并不是一种测度，不符合测度的基本条件：

Mutual Information

互信息用来描述两个分布之间的关联程度。

X Y交换位置，互信息大小不变。

如果X Y独立，则互信息为0。

熵是用“，”，互信息用“；”。

venn图表示熵和互信息的关系

熵的链式法则

定义：

如果各个变量之间独立：

信息的链式法则

条件互信息：

信息的链式法则可以将复杂的多变量的互信息转化为简单的变量少的：

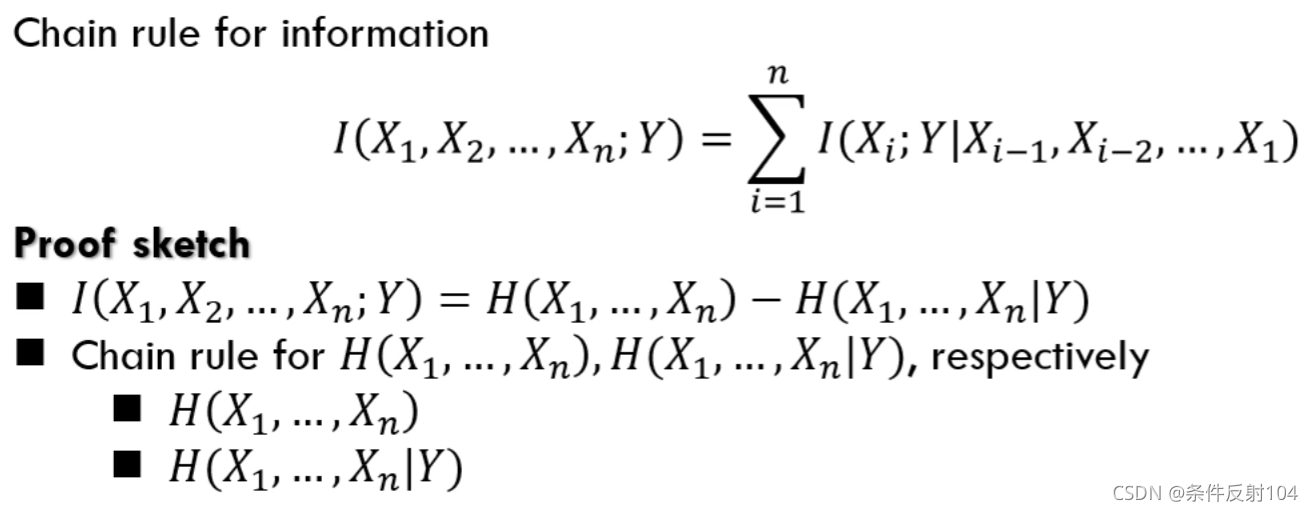
Conditional Relative Entropy

条件相对熵定义：

条件相对熵的链式法则，即先求x的相对熵，再求在x条件下y的条件相对熵，相加：

某些性质

相对熵的非负的：