【深入浅出】机器人动力学-拉格朗日方程实例

机器人动力学的两种典型方法：拉格朗日方程和牛顿欧拉方程。

拉格朗日方程的本质：基于系统的总能量去计算驱动力；

牛顿欧拉方程的本质：基于运动和力的关系去计算驱动力，牛顿方面出手的是牛顿方程（即牛顿第二定律，描述平移运动）；欧拉方面出手的是欧拉方程（描述转动运动）。

本文仅介绍拉格朗日法。首先，拉格朗日动力学方程可以表述为：

其中，代表广义力（之所以说广义，因为可以是力或者力矩），代表广义坐标（可以是角度或者长度）。L是拉格朗日函数，定义为整个系统的动能减去势能。拉格朗日动力学方程的目标就是求解那个外力f。拉格朗日方程的推导过程在多数动力学教材中都有，如果你从量纲去理解就比较简单，第一项就是“能量/(时间·速度)”，即力的量纲；第二项∂L/∂q就是“能量/位移”，也是力的量纲。

举例1：只能在垂直方向移动的质点

一个受到约束而只能在垂直线上移动的质量为m的质点 该质点的位形空间便是竖直线，因而广义坐标的一个自然选择便是质点的高度q = h，规定正方向向上。重力mg是向下作用，外界施加的作用力f按照默认方向。如果我们仅仅根据牛顿第二定律，即F=ma，不参考拉格朗日方程，也可以得出质点的动力学方程：

        好，然后我们用拉格朗日动力学方程来推导。首先拉格朗日函数等于

然后，拉格朗日动力学方程求外力：

由于包含的项只能对求导，对h求导为0；包含h的项只能h求导，对求导为0。所以

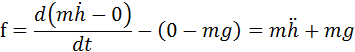
可以看到和牛顿第二定律的推导结果一致！

举例2：受到重力和关节力矩的平面2R开链机器人

（附图来自《现代机器人学》）

该运动链在xy平面内运动，重力g则作用于-y方向。在导出动力学方程之前，我们必须指定所有连杆的质量和惯量属性。为了保持模型的简明，两个连杆被视为各自质量集中于各连杆末端的点质量m1和 m2。 按照我的习惯，我想先求一下拉格朗日函数：

这里稍微轻松一下，我们把几个速度先表示出来：

然后把这几个公式带回到拉格朗日函数中：

（1）

 别急，上式中我已经把速度都带进去了，可以看到这个式子已经比较恶心的。

这里将产生本例最大的疑问，外力有哪些？如何求？

答：首先，外力只有两个，第一关节力矩τ1和第二关节力矩τ2，这里不考虑末端受到的冲击力。如果只考虑关节力矩，那么拉格朗日公式的意义就显然了，就是让两关节获得需要的角度和角速度，来求得对应关节力矩的大小。动力学方程只需要对广义关节求偏导即可：

 
                                                           （2）

将公式（1）代入到公式（2），便可得：

上式作为关节力矩结果已经完全可以，但是作为平面2R开链机器人的动力学方程，显然还比较杂乱。

因此，将上式化简一下，可得：

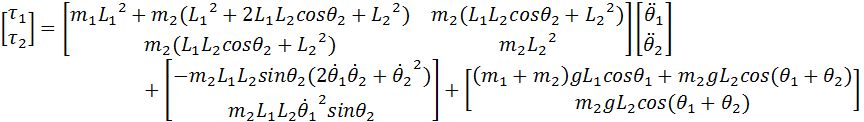
（3）

式（3）就是平面2R开链机器人的动力学方程，是以拉格朗日方程为工具进行求算的。

将矩阵块进行总结，式（3）的普遍性规律就是著名的机器人动力学方程：

                                              （4）

  式（4）对应到平面2R开链机器人，则

是质量矩阵，其中元素都是和角度θ相关的参数，没有角速度和角加速度项。准确的说，是转动惯量的量纲，是力矩的量纲。

是为包含科里奥利和向心力矩的向量。包含的二次项称为向心项，而包含的二次项则称为科里奥利项。

是包含重力矩的向量，不难看出中的项也是力矩的量纲。

机器人动力学方程（4）对于包含转动关节的串联运动链而言，通常都是正确的，而不只适用于2R型机器人。