【人脸识别】2024 AroFace: Alignment Robustness to Improve Low-Quality Face Recognition

ARoFace: Alignment Robustness to Improve Low-Quality Face Recognition

论文链接：http://arxiv.org/abs/2407.14972

代码链接：https://github.com/msed-Ebrahimi/ARoFace

一、摘要

  为了提高低质量（LQ）人脸图像的人脸识别（FR）效果，最近的研究建议在训练时加入合成的人脸图像。尽管这一方法很有前景，但这些研究考虑的质量因素较为通用，例如大气湍流、分辨率等，而不是专门针对FR的质量因素。受当前 FR 模型即使在 LQ 图像中出现较小的面部对齐误差（FAE）也会产生脆弱性的观察启发，提出了一种简单而有效的方法，将FAE作为专门针对FR的另一个质量因素。旨在通过提高FR 模型对 FAE 的鲁棒性来改善LQ FR 的效果。为此，将该问题形式化为FR 中的可微空间变换和对抗性数据增强的组合。使用可控的空间变换扰乱训练样本的对齐，并使用表达FAE的样本来丰富训练集。在 IJB-B、IJB-C、IJB-S (+4.3% Rank1) 和 TinyFace (+2.63%) 上进行的评估结果证明了所提出的方法的有效性。

二、创新点

  关键问题：当前最先进（SOTA）模型在IJB-S [31] 和 TinyFace [5]（即 LQ 基准测试）上的报告性能 [41, 55] 要比LFW [25]（即高质量（HQ）基准测试）低约 30%。这种缺陷源于训练数据和 LQ 测试数据之间的分布差异，即在训练过程中缺乏足够数量的LQ 样本。

 旨在开发一种对 FAE 鲁棒的FR 模型，称为 Alignment Robust Face（ARoFace）识别。该工作受到对抗性数据增强的启发，该增强通过将对抗性组件集成到训练过程中来增强模型的鲁棒性 [19,72]。具体来说，ARoFace 采用可微
空间变换 [28] 对训练样本的对齐进行对抗性扰动，并通过表达FAE 的样本来丰富训练。

• 引入了 FR 的特有图像退化因素 FAE，而在之前的LQ FR 研究中,这一因素被忽略了。

• 提出了一种专门针对增强 FR 模型对 FAE 的鲁棒性进行优化的方法。

• 证明了所提出的优化可以在IJB-S和TinyFace 等真实场景 LQ 评估中显著提高FR 性能。此外，该框架在不牺牲 IJB-B 和 IJB-C 等同时包含 HQ 和 LQ 样本的数据集上的性能的情况下实现了这些改进。

• 所提出的方法是一个即插即用的模块，为 SOTA FR方法提供了更好的改进。
  

三、原理

  该工作关注人脸识别模型，还拓展了低质量（LQ）输入对人脸检测和对齐的影响。

  研究表明，随着 LQ 输入的增加，人脸检测器的准确性会降低，从而导致人脸对齐错误(FAE) [10,35,59,70,85]。我们通过手动向原始对齐评估人脸添加小随机空间扰动（包括缩放、旋转和平移）来研究 FAE对 FR 性能的影响，如图 1a 和 b 所示。结果显示，如图 1c、d 和 e 所示，给定模型在对齐扰动样本和对齐样本之间的性能差距。基于这些观察结果发现，虽然最先进的人脸识别（FR）网络对高质量（HQ）人脸中的FAE 具有鲁棒性，但它们容易受到 LQ 样本中 FAE 的影响，例如，在IJB-B 和 IJB-C 上，当虚假接受率 (FAR) 为 1e−5 时，真实接受率 (TAR)下降超过50%ĂĆ（TAR@FAR=1e-5）。

  结论：FAE 是 FR 模型在 LQ 人脸识别失败中的关键因素。

  当前的FR 模型极易受到 FAE 和 LQ 输入的交叉影响。一种潜在的解决方案是同时训练识别和检测网络。

  对来自 IJB-B 数据集 (a) 对齐和 (b) 扰动对齐样本的视觉比较。(c, d, e) 在对齐输入和带有轻微特征位齐误差 (FAE) 的输入之间性能差异。模型对高质量样本中的FAE 具有鲁棒性，但在低质量人脸上表现显著下降，TAR@FAR = 1e−5 下下降超过50 %。这是使用 ArcFace/AdaFace 目标在MS1MV3 上训练的两个不同 ResNet-100 模型的结果。

Proposed Method

3.1 Notation

  本文使用小写字母$（e.g.,，x）$表示标量，小写粗体$（e.g.,，x）$表示向量，大写字母$（e.g.,\mathrm{X}）$表示函数，大写花体符号$（e.g.,\chi ）$表示集合。

  设$D={(x_n,y_n)}_{n=1}^{n_0}$ 为训练数据集，由 $n_0$ 个来自 $c$ 个类别的对齐人脸组成。此外，$F_{\psi }=C\odot E$ 表示一个具有可训练参数 $\psi =[{\psi }_1,{\psi }_2]$ 的深度神经网络，其中$E_{{\psi }_1}(\cdot ):R^q\to R^d$ 是深度特征提取器，它将输入的人脸$x\in R^q$ 映射到一个$d$维的表征（representation）$z\in R^d$，$C_{{\psi }_2}:R^d\to R^c$是一个参数化分类器（parametric classifier），即 FR 中的常规超球面分类器（hyperspherical classifier）[11,42,62]，其参数 ${\psi }_2$ 将 $\mathbf{z}$ 映射到 $c$ 个类别上的概率分布。为简洁和表述方便，所有表征均进行了 $\ell 2$ 归一化。

3.2 Preliminaries

  提出通过提高对面部对齐误差（FAE） 的鲁棒性来增强 LQ 人脸识别。提出的方法将 FAE 视为另一个针对人脸识别任务量身定制的图像质量因素，并利用对抗数据增强(adversarial data augmentation)与可微空间变换(differentiable spatial transformation) 的结合，以富含表达FAE 的样本来丰富训练过程。

  Adversarial Data Augmentation 旨在在无需额外数据的情况下改善训练效果 [7,44,49]。具体来说，它试图从原始样本 $x$（良性）中构建困难的训练实例（对抗样本）。
$${\theta }^{\ast }=argma{x}_{\theta }L(F_{\psi };T_{\theta }(x),y),\text{\hspace{1em}(1)}$$
其中 $T_{\theta }(\cdot )$ 是一个具有参数 $\theta$ 的增强函数，$L$ 是学习目标，即经验风险。该优化问题可以通过$k$步投影梯度下降 (k-steps Projected Gradient Descent, PGD) [44] 来解决：
$${\theta }_{(k+1)}\leftarrow pro{j}_S({\theta }_{(k)+\alpha sgn({\nabla }_{{\theta }_{(k)}}L(F_{\psi };T_{{\theta }_{(k)}(x),y}))}),\text{\hspace{1em}(2)}$$

其中$sgn(\cdot )$表示符号函数（sign function），$\alpha$是PGD的步长（step size），
$S$是被允许的扰动集合（set of allowed perturbation），$pro{j}_S(s)$将$s$投影回$S$，$pro{j}_S(s)=argmi{n}_{s\prime \in S}=||s-s\prime |{|}_2$。通常，$S$被定义为以$x$为中心的${\ell }_p$范数球（ℓ_{p}-norm ball），半径为$\rho$：
$$S=\theta |||T_{\theta }(x)-x|{|}_p<=\rho .\text{\hspace{1em}(3)}$$

  Spatial Transformation.详细介绍了应用于每个输入数据通道的空间变换，$x\in R^q$，其中 $q$ 是 RGB 输入的$3\times h\times w$。

  设行和列索引 $(i,j)$ 表示点$(u,v)\in R^2$，其中 $u$ 轴和 $v$ 轴分别是水平和垂直轴。此外，$P_u(j)=j-\frac{w-1}{2}$和 $P_v(i)=\frac{h-1}{2}-i$ 将零索引的$(i,j)$ 转换为 $u$,$v$ 坐标。

$T_{\theta }$ 是一个可逆的仿射变换，其参数为 $\theta =(\varphi ,\Delta u,\Delta v,\lambda )$，其中 $\varphi \in [0,2\pi ]$表示旋转角度，$∆u\in R$、$\Delta v\in R$分别表示水平和垂直平移，$\lambda \in R$和 $\lambda >-1$ 表示缩放因子 [77]。

  对于每个位置 $(P_u(j),P_v(i))$，可以通过以下公式获得在该位置下映射的坐标：
$$(u^{\prime },v^{\prime })=T_{\theta }^{-1}(P_u(j),P_v(i)),\text{\hspace{1em}(4)}$$
其中 $T_{\theta }^{-1}$ 是逆变换。$(u\prime ,v\prime )$ 可能与输入图像中的整数像素索引不对齐，因此，可以使用 Jaderberg et al. [28] 提出的双线性插值核：
$$I_x(u,v)=\sum _{i=0}^{h-1}\sum _{j=0}^{w-1}{x}_{i,j}\cdot max(0,1-|v-P_v(i)|)cdotmax(0,1-|u-P_u(j)|),\text{\hspace{1em}(5)}$$
其中$x_{i,j}$ 表示$x$ 中任意通道的第$i$ 行和第$j$ 列的像素值，因此变换后图像 $x\prime$中每个像素为：
$$x_{i,j}^{\prime }=I_x(T_{\theta }^{-1}(P_u(j),P_v(i)),\text{\hspace{1em}(6)}$$
详细推导过程参见[28]。稍微滥用一下记号，将 $x\prime =T_{\theta }(x)$ 称为 $x$在变换$T_{\theta }$下的变换版本。

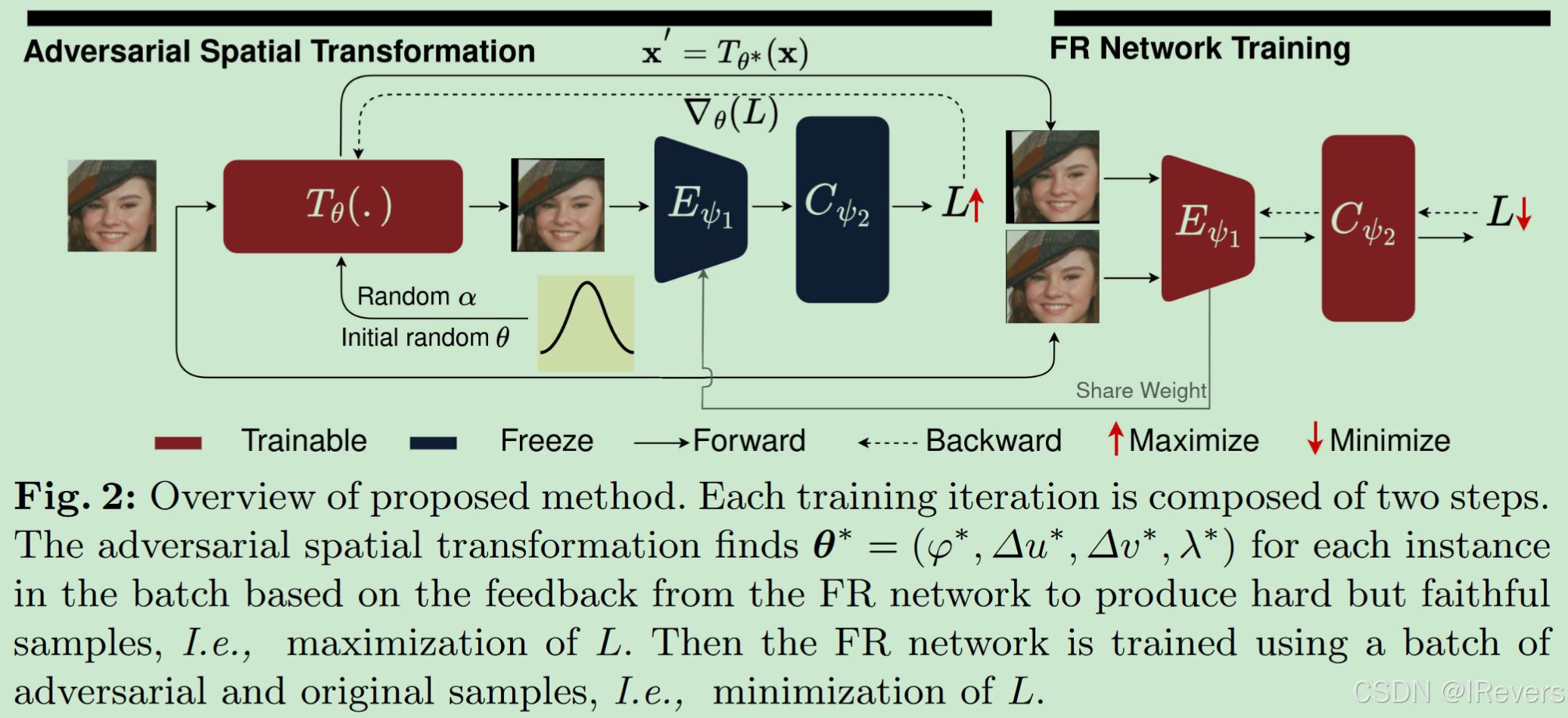
3.3 Alignment Robust Face Recognition

  如图1所示，传统的面部识别（FR）网络对低质量（LQ）人脸中甚至是轻微的人脸对齐错误（FAE）也很敏感。FAE 是 LQ 图像中无法避免的现象[10,35,59,70,85]，因此这种脆弱性是LQ FR 失败的主要原因。之前有关 LQ FR 的研究工作 [4,18,41,54,65,83,84] 忽略了 FAE，只是试图使 FR model 对一般图像质量因素（如分辨率、大气湍流、模糊等）具有鲁棒性，而这些因素并非针对 FR 而设计。将 FAE 视为另一种降损组件，并试图通过使 FR model 对 FAE 具有鲁棒性来提高LQ FR 的性能。为此，直观的解决方案是使用未对齐的人脸或对已对齐样本进行随机空间变换。然而，研究表明，在大多数 FR 评估中，随机数据增强效果不佳。

  作者旨在通过丰富表达FAE 的样本来增强 FR 网络对 FAE 的鲁棒性。为此，利用对抗数据增强（如 3.2 节所述）与可微空间变换 $T_{\theta }(\cdot )$ [28]（如 3.2 节所述，由缩放、旋转和平移组成）相结合，来构建表达FAE 的对抗样本 [28]。形式上，找到可以为 FR 模型 构建困难样本的$\theta$，即最大化 FR 目标函数。然后，使用由良性样本和对抗样本组成的批次来训练 FR网络 $F_{\psi }(\cdot )$，即最小化 FR 目标。因此，主要优化问题可以表述为：
$$argmi{n}_{\psi }=\frac{1}{|D|}\sum _{(x,y)\in D}[L(F_{\psi };x,y)+argma{x}_{\theta }L(F_{\psi };T_{\theta }(x),y)],\text{\hspace{1em}(7)}$$
其中最大化问题使用如公式2中所解释的PDG 求解，$L$ 是任意FR 目标函数，例如 ArcFace。

  在构建对抗样本 $x\prime =T_{{\theta }^{\ast }}(x)$，即公式7 中的最大化问题时，作者不希望 $x\prime$ 与 $x$ 无法区分，但它应该位于有效训练实例的流形上。然而，最大化问题可能会破坏输入图像的所有特征。例如，$T_{{\theta }^{\ast }}$ 可能会将图像清零，从而导致学习不可行。通常，良性样本与对抗样本之间的${\ell }_p$范数差异被用来定义允许的扰动集 $S$，如公式3 所示。该约定基于这样一个事实：当两幅图像在 ${\ell }_p$ 范数方面接近时，它们在视觉上也会相似 [19]。然而，它的逆命题并不总是成立，即在 ${\ell }_p$ 范数上遥远的两幅图像在视觉上也可能相似。例如，单像素平移会导致较大的${\ell }_2$范数 [17]。因此，此处不适用受 ${\ell }_p$ 范数约束的$S$。

  因此，利用每Landmark 流（位移）矢量$f=(u\prime -P_u(j),v\prime -P_v(i))$[71] 来定义 $S$，即从$x\prime$中的Landmark 位置到其对应 $x$ 中的位置的矢量：
$$S=\theta |\sum _{p\in P}||f_p^{\theta }|{|}_2<=\sum _{p\in P}\overline{f_p},\text{\hspace{1em}(8)}$$

其中 $P$ 是人脸识别对齐中通常使用的五个特征点集合[7,11, 36, 42, 62]，$\overline{f_p}$是对应于 $p$ 的流矢量范数的上界。通常，人脸识别训练样本已经对齐到预定义的模板 ‘template‘ 上，也就是说，$x$ 中的特征点位置 ‘landmarks‘ 是已知的。此外，可以通过公式4计算转换后的最终特征点位置。因此，该约束不需要特征点估计，可以使用人脸识别对齐模板（即在大型数据集中通用）和公式 4 有效地计算 $S$。补充材料的第 1 节详细解释了 $S$。

  此外，为了给构建的$T_{\theta }$ 引入不确定性，PGD 步长$\alpha$从高斯分布$ N(\mu,\delta^{2})$ 中随机采样：
$${\theta }_{(k+1)}\leftarrow pro{j}_S({\theta }_{(k)}+\alpha sgn({\Delta }_{{\theta }_{(k)}}L(F_{\psi };T_{{\theta }_{(k)}}(x),y)));s.t.\alpha N(\mu ,{\delta }^2),\text{\hspace{1em}(9)}$$

  随机化（randomized）的$\alpha$显着提高了 ARoFace 生成变换的多样性。这种多样性对于丰富表达FAE 固有不确定性的样本训练至关重要。在使用公式9获得对抗性变换参数后，使用包含良性和对抗性样本的批次来训练 $F_{\psi }$，最小化公式7。该框架通过表达FAE 的空间变换丰富了训练过程。因此，它提高了模型对 FAE 的鲁棒性，从而提升了 LQ 人脸识别（FR）性能。所提方案与 FR 训练目标正交，在不考虑身份保留和依赖先验定义的目标数据集的情况下提高了 LQ FR 的性能。整个过程如图 2 和算法 1 所示。

四、实验

4.1 Dataset

  利用了由 [11, 14] 提供的MS-Celeb-1M [21] 的清理版本作为训练数据集，即MS1MV3。该数据集由 90,000 个身份的近500 万张图像组成。根据传统的FR 框架，该工作中使用的所有数据集都对齐并转换为112 ×112 像素。在 TinyFace [6]、IJB-B [69]、IJB-C [45] 和 IJB-S [32]数据集上对 ARoFace 进行了评估。

TinyFace [6] 是一个 FR 评估数据集，由 5,139 个身份的169,403 张 LQ 人脸图像组成，用于 $1:N$ 识别。该数据集平均图像大小为 $20\times 16$ 像素。

IJB-B 和 IJB-C。IJB-B [69] 包含大约 21,800 张图像（11,800 张人脸和10,000 张非人脸）和 7,000 个视频（55,000 帧），代表了总共 1,845 个身份。

IJB-C [45] 是 IJB-B 的扩展，包括 31,300 张图像和 117,500 帧来自 3,531个身份。IJB-B 和 IJB-C 包含 HQ 和 LQ 样本，已被广泛用于评估 FR 模型 [36]。

IJB-S[32] 被公认为是最具挑战性的FR 基准之一，主要利用来自真实监控视频的样本，见图3.4a。该数据集由 202 个身份的350 个监控视频组成，总计30 小时。此外，每个受试者有七张 HQ 照片。该数据集的特点可以概括为三个关键词：

• 监控: 指使用监控视频录像。

• 单张: 表示使用单张高质量登记图像。

• 预约: 从不同视角拍摄的多张登记图像（booking）

4.2 Implimentation Details

  采用 ResNet-100 的修改版本 [11] 作为主干网络。采用 ArcFace 损失函数进行了28 epoch的训练，除非另有说明。使用SGD 作为优化器，采用从0.1 开始的余弦退火学习率、0.0001
的权重衰减和 0.9 的动量。

  $\theta$ 中控制尺度变换的组件使用 $N(\mu =1,{\delta }^2=0.01)$ 初始化，而旋转和平移的参数则从 $N(\mu =0,{\delta }^2=0.01)$ 导出。$\alpha$ 从$N(\mu =0,{\delta }^2=0.01)$中采样。补充材料第 2 节提供了有关这些参数的详细实验。

  在训练过程中，每个 GPU 处理大小为 512 的mini-batch，利用 4 个 Nvidia RTX 6000 GPU。为了公平比较，当无法获得特定方法的检查点时，使用了作者发布的官方代码及其出版物中推荐的最佳超参数来重现他们的结果。

4.3 Comparison with SOTA Methods

  表1 将 ARoFace 在 IJB-B、IJB-C 和TinyFace 上的性能与 SOTA 方法进行了比较。这些结果表明，ARoFace 在各种指标和数据集上提出了新的SOTA 基准。这些利用不同训练数据集取得的进步表明，ARoFace的优势不局限于任何特定的训练数据集。在使用WebFace4M、MS1MV3 和MS1MV2 训练集时，ARoFace 在 IJB-B 上对应 FAR=1e −6 的情况下分别比其竞争对手高出 0.43%、2.04% 和 1.43%。具体来说，在 IJB-C 上，ARoFace 使用 WebFace4M 高于 AdaFace 的幅度为 1.14%，使用 MS1MV3高于 ArcFace 的幅度为 0.49%（FAR=1e −6）。将 MS1MV2 作为训练数据，ARoFace（ArcFace+ARoFace）分别比 CFSM [41]（ArcFace+CFSM）高出 2.63% 和 3.65%（Rank1 和 Rank5 TinyFace 识别）。这些优于 CFSM的增强功能（优先在训练中包含合成 LQ 数据）强调了减少对 FAE 的敏感性比引入 LQ 实例到训练中更为重要。

  通过将 WebFace4M 作为训练数据，ARoFace 在 TinyFace 评估中分别将 AdaFace 的性能提升了 1.82% 和 2.11%，这在 Rank1 和 Rank5 中表现明显。此外，将 WebFace12M 作为训练数据时，ARoFace 分别将 AdaFace的性能提升了 2.35% 和 2.5%，在 Rank1 和 Rank5 中同样表现突出。这些一致的提升表明，随着数据集大小的增加（即从 400 万张图像增加到 1200万张图像），ARoFace 仍然保持着有效的性能。

  ARoFace 在 TinyFace 上的性能达到了顶峰，同时在IJB-B 和 IJB-C 基准测试中也没有降低性能，在大多数验证和识别指标上超过了其竞争对手。IJB-B 和 IJB-C 数据集包含 HQ 和 LQ 两种人脸 [36]，如图3b所示。因此，在 IJB-B、IJB-C 和 TinyFace 数据集上的一致性提升表明了 ARoFace 的泛化能力，以及它在提升 LQ 人脸识别性能的同时，仍能保持在 HQ 人脸识别上的高性能。

  表2显示了 ARoFace 在 IJB-S 数据集上的性能与其竞争对手的比较。ARoFace通过显著超越之前的基准性能，创造了新的先进性能。特别是，ARoFace 使用了MS1MV2 训练集，超越了ArcFace 基线，在Surveillance-to-Single 和Surveillance-to-Booking 验证中分别提高了6.02%和5.11%。这一显著进步不仅凸显了类似IJB-S 这样的LQ 基准测试中的人脸对齐挑战，而且证明了所提方法能够提高人脸识别模型对部分人脸遮挡的鲁棒性。

  在 IJB-S 数据集上的各个指标上所表现出的一致性提升，突显了部分人脸遮挡对现有先进人脸识别模型区分能力的影响，例如 ArcFace 和AdaFace。在不同的训练数据集上观察到的这些性能提升表明，提出的方法的有效性不受训练集的限制。

4.4 Analysis on Robustness to Face Alignment Error

  人脸对齐是几乎所有可用的人脸识别模型必不可少的先决条件。在图1中，以经验的方式展示了SOTA人脸识别网络即使在 IJB-B 和 IJB-C 中受到轻微的人脸对齐误差 (FAE) 影响时也会出现严重的脆弱性。

  这里进一步检验了 ARoFace 在增强模型对 FAE 的鲁棒性方面的有效性。表3 比较了ArcFace 和AdaFace 在其原始训练方案和修改后的训练方法下所取得的表现。引入ARoFace 显著提升了这两种方法对FAE 的鲁棒性。具体来说，在 IJB-B 和 IJB-C 中，ArcFace 在扰动图像上的性能分别提高了 15.35% 和 12.75%（TAR@FAR=1e−5），以及 7.21% 和 15.61%（TAR@FAR=1e −4）。同样，Adaface 在扰动图像上的性能也有提升，分别提高了 32.9% 和 18.03%（TAR@FAR=1e −5），以及 27.56% 和 45.4%（TAR@FAR=1e −4）。

  这些显著的提升证明了所提出的方法在增强人脸识别网络对 FAE 的鲁棒性方面的有效性。值得注意的是，在人脸识别模型的训练中采用经典的增强技术会导致模型泛化能力下降 [36,41,51]。集成 ARoFace不仅提升了对齐和对齐扰动输入的性能，这一一致性的提升尤为显著，它强调了所提出的方法的泛化能力，并凸显了 ARoFace 在增强对 FAE 的鲁棒性的同时，不会牺牲对齐样本的表现。

4.5 Orthogonal Improvement to Angular Margin

  ARoFace 的目标是通过在训练中注入对齐样本来提高低质量人脸识别的性能。图 3c 显示了原始样本和增强样本的对比。这里评估了 ARoFace 在不同角度范围下的有效性，如图 3d 所示。具体来说，作者修改了三种最先进的方法（即 CosFace、ArcFace 和 AdaFace）的训练代码，将训练策略集成到其中，并使用 CASIA-WebFace [81] 作为训练数据。这些结果表明了 ARoFace 与现有角度惩罚损失的正交性。因此，ARoFace 可以无缝集成到最先进的人脸识别框架中，成为即用型模块，提高它们对人脸对齐误差的鲁棒性，并最终提高性能，特别是在低质量评估方面。

4.6 Runtime Overhead

  与 [41,54] 相比，所提出方法的一个显著优点是它可以绕过对复杂图像生成过程的需要，该过程需要两步优化，即训练生成器，然后将其集成到人脸识别训练中。所提方法直接对输入图像进行仿射变换 [28]，从而消除了两步优化的需要。

  ARoFace 仅使用了四个额外的可训练参数，导致计算负载的可忽略不计的增加。额外的计算时间和内存消耗的大部分原因是对抗训练。在图 4a 和 b 中，我们将所提方法与 Liu et al. [41] 的CFSM 进行了比较，后者也旨在增强 LQ FR。通过避免使用图像生成模型，即 [41] 中的GAN，所提方法将 CFSM [41] 的训练速度提高了 25%，并减少了内存消耗 35%。训练速度的显著提高和内存消耗的减少，再加上表3 和4所示的性能改进，突出了我们的方法在大规模FR 中的能力。

  此外，还将 (ArcFace+CFSM+ARoFace) 与原始 CFSM 设置 (ArcFace+CFSM) 进行了比较。CFSM 已经使用了对抗优化。因此，如图4a、b 所示，将 ARoFace 集成到 CFSM 中会导致训练速度略有下降，而内存使用则会增加。从 ARoFace 集成中产生的额外计算工作量很小，证实了额外的计算负载来自对抗训练，这是将增强集成到 FR 训练中所需的[41]。

4.7 Ablation on Transformation Components

  3.1 节注意到 ARoFace 采用的空间变换包括缩放、旋转和平移。这里研究每种组件对 ARoFace 性能的影响，即每个变换组件对性能提升的贡献程度。为此，在 TinyFace 上进行了消融研究，使用 ArcFace 作为损失函数，并将 CASIA-WebFace [81] 作为训练数据集。如表4所示，这些实验表明，缩放是收益最大的变换，能将性能提升近5%。这与先前的研究 [36,41,54] 一致，突显了缩放在生成 LQ 输入中的作用。平移和旋转分别贡献了约 3% 的性能提升，反映了它们对面部对齐的类似影响。

4.8 Random vs. Adversarial

  liu et al. [41] 表明，没有对抗性优化（即随机生成 LQ 样本）时，性能提升微不足道。这里在图4c、d 和 e 中在提出的框架中研究这种效果。结果表明，使用空间增强（无论是随机增强还是带有对抗性信号的增强）均可提高LR 输入（即 TinyFace）的基线识别性能。然而，随机增强会破坏 FR 模型对 HQ 样本的辨别力，即 IJB-B 和 IJB-C 数据集上的识别率急剧下降。采用 ARoFace 的可微空间变换的主要优势是能够在具有
不同图像特征的数据集（即 IJB-B、IJB-C、IJB-S 和 TinyFace）上取得性能提升，且不会牺牲对齐样本上的性能以获得对 FAE 的鲁棒性。

4.9 Effect of Random Sampling of \alpha

  表 5 比较了 ARoFace 在使用和不使用随机采样的 $\alpha$ 情况下的性能。在这些实验中，当 $\alpha$ 是固定的时，其值等于随机分布的平均值，即 ${\alpha }_{random}\sim N(\mu ,{\delta }^2)$，${\alpha }_{fixed}=\mu$。在 TinyFace 中，使用 ${\alpha }_{random}$ 明显优于 ${\alpha }_{fixed}$。这一显着的改进突显了低质量图像中人脸对齐误差的多样性，通过 ${\alpha }_{random}$ 引入的不确定性有助于 ARoFace 提高对人脸对齐误差的鲁棒性。此外，IJB-B 和 IJB-C 数据集上的性能在两种情况下几乎相同。作者认为这是因为这些数据集是低质量和高质量人脸图像的混合。

五、总结

  本文基于对当前 FR 模型易受 LQ 人脸 FAE 影响的观察，提出将 FAE 视为另一种专门针对 FR 的图像降级因素。该方法结合了可微的空间变换和对抗性数据增强来制作表达FAE 的样本，并将其添加到 FR 模型的训练中。这种框架允许FR 模型在训练过程中接触到 FAE，并提高对 FAE 的鲁棒性。通过在包括 IJB-B、IJB-C、IJB-S 和 TinyFace在内的不同基准上进行各种实验和评估来评价所提出的方法的有效性。

Supplementary Materials

  按照惯例，在训练人脸识别模块之前会进行人脸检测和对齐，根据对齐模板确保所有训练实例中关键点位置的一致性。因此，关键点的原始位置$(u_p,v_p)$与对齐模板的位置一致。此外，如公式（4）所述，通过应用可逆仿射变换$T_{\theta }$，可以确定关键点最终位置。因此，可以通过考虑变换组件的上限（即最大允许的旋转、平移和缩放）来计算位移向量上限$\bar{\mathbf{f}}$ ：
$$\overline{{\mathbf{f}}_p}=(u_p^{\prime }-u_p,v_p^{\prime }-v_p);(u^{\prime },v^{\prime })=T_{{\bar{\theta }}^{-1}(P_u(j),P_v(i))},0\text{\hspace{1em}(1)}$$
其中$\theta$ 表示转换参数的上限，即最大旋转、缩放和平移。同样地，在训练过程中计算位移矢量来定义 $S$：
$${\mathbf{f}}_p^{\theta }=(u_p^{\prime }-u_p,v_p^{\prime }-v_p);(u^{\prime },v^{\prime })=T_{\theta }^{-1}(P_u(j),P_v(i)),1\text{\hspace{1em}(1)}$$
最后，${\bar{f}}_p=||{\bar{\mathbf{f}}}_p|{|}_2$，在不需要关键点估计的情况下，使用文中的公式8来定义允许的变换。

1 Experiment on Upper Bound of Individual Transformations

  利用预定义的人脸对齐模板，允许的扰动集 $S$ 直接与 $\bar{\theta }$ 相关联，后者定义了各个转换的最大允许值。这里在表6中对转换 $T_{\theta }$ 的各个组件（即缩放、平移和旋转）的上限进行了实验。结果表明，随着不同组件的上限增加，TinyFace 的性能也得到了一致性的提升。此外，与FR 性能中增强效果方面先前的研究 [36, 41, 54] 一样，缩放对 TinyFace的性能有更显著的影响。此外，结果表明，在包含 HQ 和 LQ 实例的数据集上的性能容易受到转换上限高值的影响，导致性能显著降低。这是由于这些数据集中图像的性质造成的。由于这些基准测试中同时存在 HQ 和 LQ 样本，过度的增强降低了 FR 模型对 HQ 图像的区分能力，从而降低了这些评估中的性能。

2 Experiments on Perturbation Budgets

  实验以评估扰动预算$\alpha$对空间变换各组成部分（如图5所示，为尺度、旋转和平移）的影响。使用 CASIA-WebFace 作为训练数据集，并将 ArcFace 作为目标。实验结果表明，尺度预算与 TinyFace性能之间存在正相关关系；具体来说，较大的尺度预算显着提高了 Rank1 TinyFace 识别精度。这一结果在意料之中，因为较大的尺度扰动会产生较小的脸部，从而提高LQ 样本的性能。

然而，尺度预算的持续增加导致 IJB-B 和 IJB-C 数据集上的验证性能显着下降。因为 IJB-B 和 IJB-C 包含 HQ 和LQ 图像，而严重的尺度变化会降低 HQ 图像的辨别力 [36,41,51]。为了获得具有泛化能力的FR 模块，选择了 0.01 的尺度预算。此外，旋转预算为0.01 在IJB-B 和IJB-C 评估中表现出优异的性能，这表明HQ 样本中可能存在错位。此外，平移预算为 0.01 在 TinyFace 和其他数据集上都取得了均衡的性能。CNN 在一定程度上对平移具有不变性，这部分是池化操作特性所导致的。因此，这种微小的扰动有助于增强模型对错位鲁棒性。重要的是，极端平移可能会使脸部重要部分变为零，从而无法学习，而旋转则不会去除图像的任何部分。

  表7研究了$k$在TinyFace、IJB-B和IJB-C上的性能影响。实验使用$k\in 1,2,3$。如表3所示，PGD步骤增加带来的性能提升微不足道。然而，计算开销随着PGD步骤数的增加而急剧增加。因此，在所有实验中采用$k=1$。IJB-B和IJB-C上的性能微小下降与 [36,41,51]的观察结果一致，即这些数据集包含HQ和LQ实例，过多的输入增强会导致性能下降。