【图形学】 06 四元数（一）

参考：quaternion.pdf和3B1B的视频

1、四元数记法

  一个四元数包含一个标量分量和3D向量分量，有两种记法：
$$\begin{gathered} [w,\text{v}] \\ [w,(x,y,z)] \end{gathered}$$

2、复数的共轭（Conjugate）和模长（Magnitude）

  我们有复数 p ：$p=(a+bi)$，其共轭表示为：$ p^*=(a-bi)$。这样我们就能更好的计算复数的模：
$$\begin{gathered} ||p||=\sqrt{p{p}^{\ast }} \\ ||a+bi||=\sqrt{(a+bi)(a-bi)} \\ =\sqrt{a^2+b^2} \end{gathered}$$

3、复数的乘法

  对于两个复数：$z_1=a+bi$、$z_2=c+di$相乘，我们可以使用分配律来计算它们的乘积：
$$\begin{gathered} z_1{Z}_2=(a+bi)(c+di) \\ =ac+adi+bci+bd{i}^2 \\ =(ac-bd)+(bc+ad)i \end{gathered}$$
  观察能够轻易发现，复数相乘的结果其实也是一个矩阵与向量相乘的结果，也就是说：
$$\begin{gathered} z_1{z}_2=(ac-bd)+(bc+ad)i \\ =\left[\begin{array}{cc}a& -b\\ b& a\end{array}\right]\left[\begin{array}{c}c\\ d\end{array}\right] \end{gathered}$$
  这个式子中，右侧的$\left[\begin{array}{c}c\\ d\end{array}\right]$是用向量的形式来表示 $z_2$，而左侧的$=\left[\begin{array}{cc}a& -b\\ b& a\end{array}\right]$则是用来表示 $z_1$ 的，所以，“复数和复数的乘法”可以看作，一个复数对另一个复数所进行的拉升变换。也就是对复平面上的一个点进行旋转和缩放~

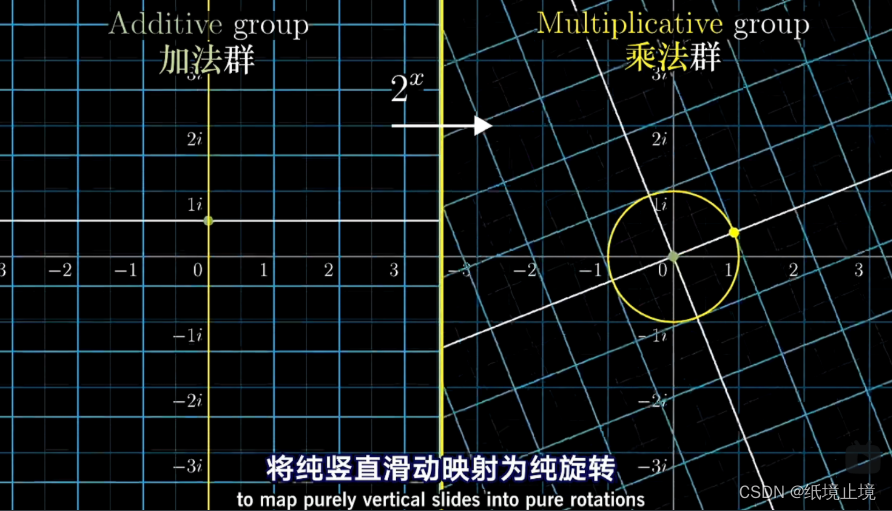
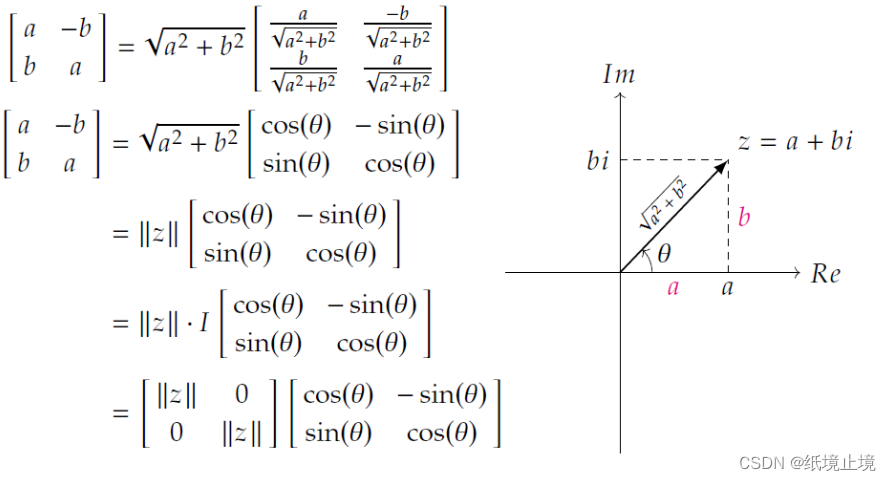
  所以，复数相乘其实就是 旋转与缩放变换的复合 。对于一个复数 $z=a+bi$，结合图像和它与 x 轴的角度 $\theta$ ，我们就能转换成 缩放矩阵和旋转矩阵的形式

  所以，我们说：对于任意一个复数 $z=a+bi$ ，任何一个复数 $v=x+yi$ 与它相乘，都会被逆时针旋转 $\theta =atan2(b,a)$度，并缩放$||z||=\sqrt{a^2+b^2}$ 倍。我们可以构造得到一个等价的复数乘法来表示这样的矩阵变换了：

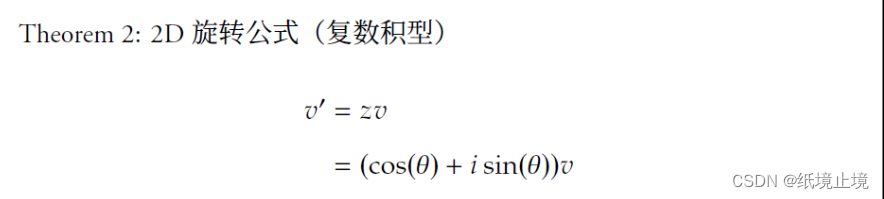
4、复数的极坐标型

  根据欧拉公式（Euler’s Formula）：$cos(\theta )+isin(\theta )=e^{i\theta }$。对于我们的复数就有：

  所以，我们有：

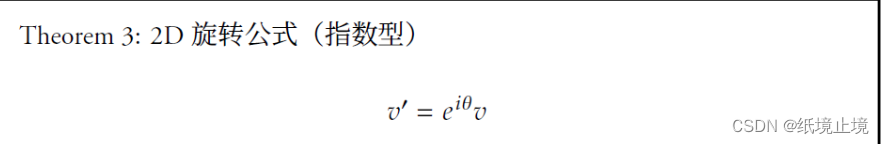
5、三维坐标系的旋转

  假设我们有一个经过原点的（如果旋转轴不经过原点我们可以先将旋转轴平移到原点，进行旋转，再平移回原处）旋转轴 $\text{u}=(x,y,z{)}^T$ ，我们希望将一个向量 $v$，沿着这个旋转轴旋转 $\theta$ 度，变换到 $v^{\prime }$：

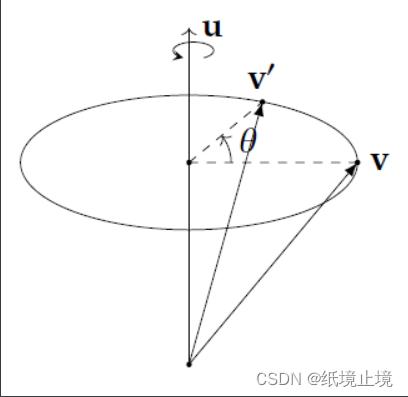
  在轴角的表示方法中，一个旋转的定义需要使用到四个变量：旋转轴 $\vec{u}$ 的 x,y,z 坐标，以及一个旋转角 $\theta$，也就是我们一共有四个自由度（Degree of Freedom）。这很明显是多于欧拉角的三个自由度的。实际上，任何三维中的旋转只需要三个自由度就可以定义了，为什么这里我们会多出一个自由度呢？
  其实，在我们定义旋转轴 $\vec{u}$ 的 x,y,z 坐标的同时，我们就定义了 $\vec{u}$ 的模长（长度）。然而，通常情况下，如果我们说绕着一个向量 $\vec{u}$ 旋转，我们其实指的是绕着ū所指的方向进行旋转。回忆一下向量的定义：向量是同时具有大小和方向的量，但是在这里它的大小（长度）并不重要。所以，这里实际上还是只有三个 自由度。

  为了消除旋转轴ū模长这个多余的自由度，我们可以规定旋转轴 $\vec{u}$ 的模长为 $\Vert \vec{u}\Vert =\sqrt{x^2+y^2+z^2=1}$，也就是说u是一个单位向量。这样一来，空间中任意一个方向上的单位向量就唯一代表了这个方向。我们其实可以将模长规定为任意的常量，但是规定$\Vert \vec{u}||=1$能为我们之后的推导带来很多的便利，这也是数学和物理中对方向定义的惯例。

6、四元数和 轴—角 对

  我们以 n 为旋转轴，旋转 $\theta$ 度。对于四元数的计算：
$$\begin{gathered} \text{q}=[cos(\theta /2)sin(\theta /2)\text{n}] \\ =[cos(\theta /2)sin(\theta /2){\text{n}}_{x}sin(\theta /2){\text{n}}_{y}sin(\theta /2){\text{n}}_z] \end{gathered}$$