旋转向量和平移向量的本质

旋转向量和平移向量的本质

1. 平移向量的本质

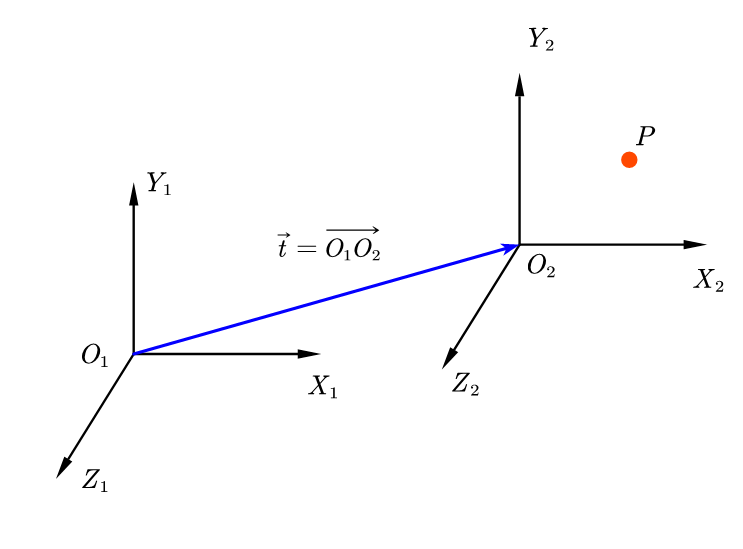
如图所示，坐标系1和坐标系2平行但不重合，所以空间点从坐标系2到坐标系1的变换只有平移，空间的一点$P$在坐标系2和坐标系1的坐标分别设为$P_2$和$P_1$，设平移向量为$\vec{t}$，即，空间点从坐标系2到坐标系1的变换可以表示为：$P_1=P_2+\vec{t}$

• 本质：空间点从坐标系2变换到坐标系1的平移向量$\vec{t}$为$\overrightarrow{O_1{O}_2}$，在坐标系1中该向量的值与$O_2$在坐标系1中的坐标相等。

2. 旋转矩阵的本质

如图所示，坐标系1和坐标系2原点重合但是不平行，所以空间点从坐标系2到坐标系1的变换只有旋转矩阵。空间的一点$P$在坐标系2和坐标系1的坐标分别设为$P_2$和$P_1$，旋转矩阵用$R$表示则：

$P_1=R{P}_2$

$R=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]=\left[\begin{array}{ccc}{r}_1& r_2& r_3\end{array}\right]$

在坐标系2中取三个特殊点$A(1,0,0)，B(0,1,0)，C(0,0,1)$，并分别将其转换到坐标系1中，则

$\{\begin{array}{l}{P}_{A1}=R{P}_A=r_1\\ P_{B1}=R{P}_B=r_2\\ P_{C1}=R{P}_C=r_3\end{array}$

空间点从坐标系2到坐标系1的旋转矩阵R的分量$r_1,r_2,r_3$分别为坐标系2的基底向量$\overrightarrow{O_2{X}_2}、\overrightarrow{O_2{Y}_2}、\overrightarrow{O_2{Z}_2}$在坐标系$O_1$中的表示。

同理：${\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\end{array}\right]}^T、{\left[\begin{array}{ccc}{r}_{21}& r_{22}& r_{23}\end{array}\right]}^T、{\left[\begin{array}{ccc}{r}_{31}& r_{32}& r_{33}\end{array}\right]}^T$分别为坐标系1的基底向量$\overrightarrow{O_1{X}_1}、\overrightarrow{O_1{Y}_1}、\overrightarrow{O_1{Z}_1}$在坐标系$O_2$中的表示。

• 空间点从坐标系2到坐标系1的旋转矩阵R的本质：
  • 列分量本质上是坐标系2的X轴、Y轴和Z轴在坐标系1中的坐标；
  • R的行分量本质上是坐标系1的X轴、Y轴和Z轴在坐标系2中的坐标。

3. 两个坐标系之间的旋转矩阵和平移向量的相互转换关系

3.1 假设

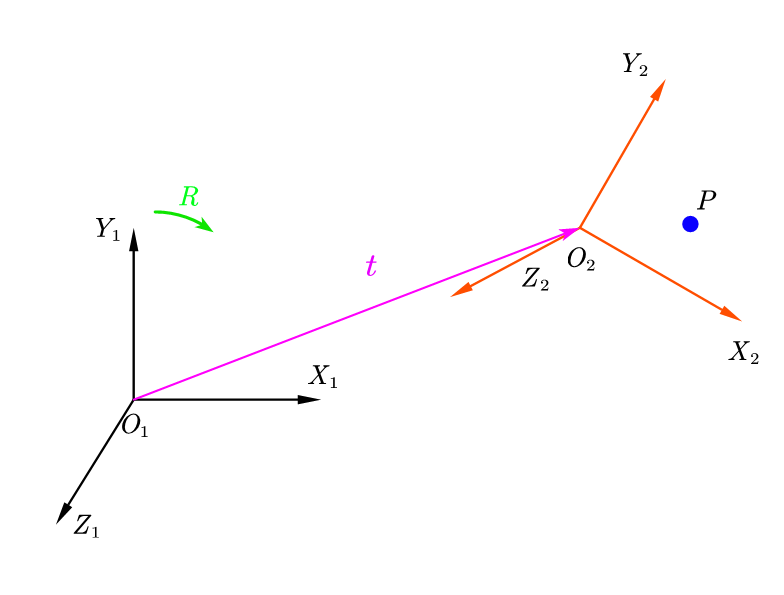
• 空间的一点$P$在坐标系2和坐标系1的坐标分别设为$P_2$和$P_1$
• 坐标系1到坐标系2的旋转矩阵和平移向量设为：$R_{1->2}$，$t_{1->2}$
• 坐标系2到坐标系1的旋转矩阵和平移向量设为：$R_{2->1}$，$t_{2->1}$

3.2 转换关系推导

• $P_2->P_1$

  • $P_1=R_{2->1}{P}_2+t_{2->1}$，变换得：
  • $P_2=R_{2->1}^{-1}{P}_1-R_{2->1}^{-1}{t}_{1->2}$

• $P_1->P_2$

  • $P_2=R_{1->2}{P}_1+t_{1->2}$

• 综上可得：

  • $\{\begin{array}{l}{R}_{1->2}=R_{2->1}^{-1}=R_{2->1}^T\\ t_{1->2}=-R_{2->1}^{-1}{t}_{1->2}\end{array}$
  • 因为标准旋转矩阵R为单位正交阵
  • 因此旋转矩阵互逆，平移矩阵大小不变方向相反