3.2.3 Synchronization of several trapezoidal trajectories 多条梯形轨迹的同步

        如果多个驱动器必须协同，那么全部轨迹必须根据最慢的那个进行规划，或者最大位移那个。例如，假设一个动作所包含的多个驱动器以同样的约束条件进行规划（同样最大加速度和速度）。在这样情况下，需要对位移最大的驱动器在最大加速度amax 条件下计算加速阶段时间Ta和总时间T。一旦时间Ta,T确定好，其余的驱动器便可以根据各自的位移hi确定各自的加速度和速度。见3.2.6节

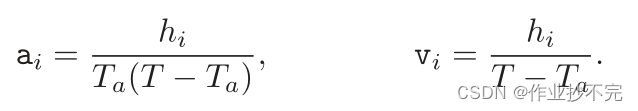
        然后公式（3.4）可以用于每条轨迹的计算 

---

        例子3.3：定义三个驱动器（具有相同的最大速度和加速度vmax = 20 、amax = 20），这三个驱动器的位移必须定义，从而保证计算出总时间T最小，三个驱动器的加速阶段或者减速阶段的时间Ta/Td相同。位移定义如下：

 

     

         a号驱动器有最大位移( = 50),因此总时间T和加速阶段/减速阶段的时间Ta/Td由此驱动器定义。因为 > /,所以匀速段存在，然后根据, 和公式(3.8)可以得到：

         然后，其余驱动器的最大/最小速度和加速度可以计算如下：

 
        注意：b号驱动器的位移为负，所以其加速和减速阶段时间互换（既先减速再加速）。此外因为对称，所以amin = −amax 和vmin = −vmax 。T, Ta 和最大加速度、最大速度可以用于计算三个驱动器的轨迹。结果见图3.4.