3.2 Linear Trajectory with Parabolic Blends (Trapezoidal) 与抛物线混合的线性轨迹(梯形)

        获得具有连续速度曲线的轨迹的一种非常常见的方法是使用混合抛物线的线性运动，因此以其特征为典型的梯形速度曲线。

        轨迹分为三部分。假设位移为正，即q1 > q0，则在第一部分中，加速度是正的、恒定的，因此速度是时间的线性函数，位置是抛物线曲线。第二部分中，加速度为零，速度为常数，位置为线性函数。在第三部分中，加速度为负常数，速度线性下降，位置是一个二次多项式，具体如图3.3所示。对于这类轨迹，通常假设加速阶段的时间Ta 等于减速段时间Td.【如果q1 < q0 ，则所有相关加速度和速度表达式需要适当变化符号，见3.4.2节】

 Fig. 3.3. 梯形速度曲线的位置、速度、加速度

        如果t0 = 0，则轨迹计算如下：

        1.加速阶段，t ∈ [0, Ta]。位置、速度、加速度公式如下：

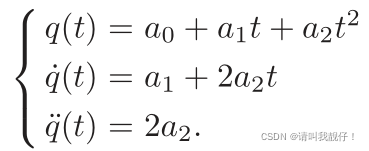                (3.1)

              公式内的三个参数a0,a1, 和a2 可以通过初始条件q0 、v0 和加速阶段末的Vv速度计算。
              假设初始速度为零，则计算如下：

                 

                 在这阶段，加速度恒定且值为Vv/Ta

        2.匀速阶段，t ∈ [Ta, t1 − Ta]。 位置、速度、加速度计算如下 ：

                

         其中，考虑连续约束条件:

                       b1 = Vv

           以及

                

            因此

                      

       2.减速阶段，t ∈ [t1−Ta, t1]。位置、速度、加速度如下：

                        

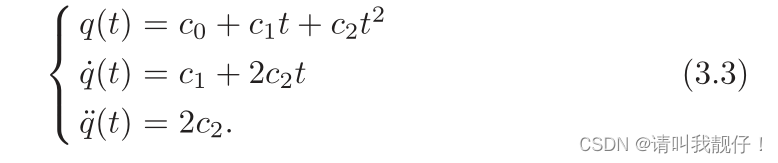
         三个参数由q1  、 v1和减速段开始出的vv  定义。假设终速度为零，可得：        

                      

             综上所述，考虑通常t0 通常不等于零，因此位置方程可以如下定义

                    

               

          Example 3.2    图3.3 展示了典型梯形速度轨迹的位置、速度、加速度。约束条件
                                           q0 = 0, q1 =30, t0 = 0, t1 = 4, Ta = 1, vv = 10.

---

        注意到一些额外的条件必须指定，以明确定义梯形轨迹。一个典型的条件是加速阶段和减速阶段的时间Ta 必须满足Ta ≤ T/2 = (t1 − t0)/2.另外还有些驱动系统的最大速度和最大加速度的条件，显然这些条件影响了轨迹是否可行。
        在任何情况下，给定的条件必须满足一些几何约束。特别的，根据t = t0+Ta 处的速度连续条件，可以得到：

                

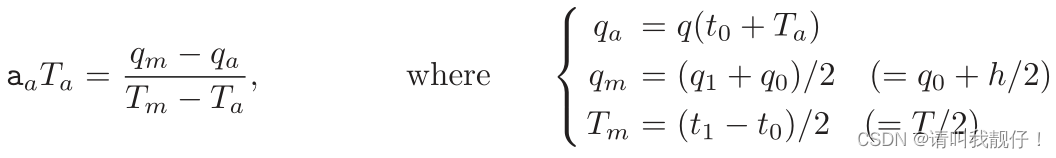
        其中是加速阶段的加速度值。
        从（3.4）公式可以得到:

                

        ​​​​​​​根据上述两个等式，很容易得到

                

        以及

                

        任何一组满足(3.5)的 (,Ta)都可以，例如指定Ta然后加速度和速度Vv可以根据公式计算出来。如果Ta = (t1 − t0)/3，则计算如下：        

                 

         如果以这种方式计算的速度Vv太大（超过实际能力），例如Vv > Vmax, 那么Ta 必须减小，然后根据（3.5）计算 ，或T (轨迹总时间)必须增大。如果加速度太大 > amax，   则Ta 必须增大。