MDS（多维尺度变换）降维算法

最新推荐文章于 2023-01-12 23:30:18 发布

qq_41267488

最新推荐文章于 2023-01-12 23:30:18 发布

阅读量3.4k

点赞数 3

文章标签：算法机器学习无监督学习

本文链接：https://blog.csdn.net/qq_41267488/article/details/120460895

版权

1.目标：

将目标的（ $1\times m$ ）维表示特征的向量降为（ $1 \times z$ ）维， $z<m$ 。

2.输入数据：

$\textbf{X}=[\textbf{x}_1^T,\textbf{x}_2^T,...,\textbf{x}_n^T]$ ，其中 $\textbf{x}_i$ 为（ $1\times m$ ）维表示第 $i$ 个目标特征的向量，我们将每一个目标看作 $m$ 维空间中的一个点，那么 $\textbf{x}_i$ 为空间中第 $i$ 个点的坐标。

3.输出数据：

$\textbf{Z}=[\textbf{z}_1^T,\textbf{z}_2^T,...,\textbf{z}_n^T]$ ，其中 $\textbf{z}_i$ 为（ $1 \times z$ ）维表示第 $i$ 个目标降维后的特征向量。

4.基本思想

将高维坐标中的点投影到低维空间中，保持点彼此之间的相似性尽可能不变。

5.方法

5.1相似性定义

在经典MDS降维算法中，点与点之间的相似性定义为两个点之间的欧几里得距离，在非经典MDS降维算法中，点与点之间的相似性定义为两个点之间的非欧几里得距离（其他距离）,我们使用 $||\textbf{x}_i-\textbf{x}_j||^2$ 表示第 $i$ 个点与第 $j$ 个点在原高维空间上的欧式距离， $||\textbf{z}_i-\textbf{z}_j||^2$ 表示他们在低维空间上的距离。

5.2推导降维后的特征矩阵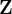 $\textbf{Z}$

（1）设降维后第 $i$ 个点与第 $j$ 个点的距离如公式（1）：

$\begin{aligned} d_{ij}&= ||\textbf{z}_i-\textbf{z}_j||^2 \\&= ||\textbf{z}_i||^2+||\textbf{z}_j||^2-2\textbf{z}_i^T\textbf{z}_j \end{aligned}$ （1）

（2）不失一般性，我们假设 $z$ 维空间中的实例点是中心化（所有点在任意一维上的坐标和为0）的，即:

$\sum_{i=1}^{N} {z_i}=\textbf{0}$ （2）

（3）公式(1)左右两边在 $i$ 上求和:

$\begin{aligned} \sum_{i=1}^{N}d_{ij}&=\sum_{i=1}^{N} ||\textbf{z}_i||^2+N||\textbf{z}_j||^2-2\sum_{i=1}^{N}\textbf{z}_i^T\textbf{z}_j \\ &=\sum_{i=1}^{N} ||\textbf{z}_i||^2+N||\textbf{z}_j||^2-2\textbf{z}_j \sum_{i=1}^{N}\textbf{z}_i^T\\ &=\sum_{i=1}^{N} ||\textbf{z}_i||^2+N||\textbf{z}_j||^2 \end{aligned}$ （3）

同理，在 $j$ 上求和

$\begin{aligned} \sum_{j=1}^{N}d_{ij}&=\sum_{j=1}^{N} ||\textbf{z}_j||^2+N||\textbf{z}_i||^2 \end{aligned}$ （4）

（4）公式(3)左右两边再在 $j$ 上求和:

$\begin{aligned} \sum_{i=1}^{N}\sum_{j=1}^{N}d_{ij}&=\sum_{i=1}^{N} \sum_{j=1}^{N}||\textbf{z}_i||^2+N\sum_{j=1}^{N}||\textbf{z}_j||^2 \\&= N\sum_{i=1}^{N}||\textbf{z}_i||^2+N\sum_{j=1}^{N}||\textbf{z}_j||^2 \\&= 2N\sum_{i=1}^{N}||\textbf{z}_i||^2 \end{aligned}$ （5）

（5）定义内积矩阵 $\textbf{B}=\textbf{Z}^T\textbf{Z}$ ，则 $b_{ij}=\textbf{z}_i^T\textbf{z}_j$ ，根据公式（1）

$\begin{aligned} &\textbf{z}_i^T\textbf{z}_j= -\frac{1}{2}({}d_{ij}-||\textbf{z}_i||^2-||\textbf{z}_j||^2)\end{aligned}$ （6）

根据公式（3）（4），

$\begin{aligned} ||\textbf{z}_i||^2 &=\frac{1}{N}\sum_{j=1}^{N}d_{ij}-\frac{1}{N}\sum_{j=1}^{N} ||\textbf{z}_j||^2\ \\||\textbf{z}_j||^2 &=\frac{1}{N}\sum_{i=1}^{N}d_{ij}-\frac{1}{N}\sum_{i=1}^{N} ||\textbf{z}_i||^2\end{aligned}$ （7）

所以，

$\begin{aligned} \textbf{z}_i^T\textbf{z}_j&= -\frac{1}{2}({}d_{ij}-\frac{1}{N}\sum_{j=1}^{N}d_{ij}+\frac{1}{N}\sum_{j=1}^{N} ||\textbf{z}_j||^2-\frac{1}{N}\sum_{i=1}^{N}d_{ij}+\frac{1}{N}\sum_{i=1}^{N} ||\textbf{z}_i||^2)\\ &= -\frac{1}{2}({}d_{ij}-\frac{1}{N}\sum_{j=1}^{N}d_{ij}-\frac{1}{N}\sum_{i=1}^{N}d_{ij}+\frac{2}{N}\sum_{i=1}^{N} ||\textbf{z}_i||^2)\ \end{aligned}$

根据公式（5）

$\begin{aligned} \frac{2}{N}\sum_{i=1}^{N}||\textbf{z}_i||^2 =\frac{1}{N^2}\sum_{i=1}^{N}\sum_{j=1}^{N}d_{ij}\end{aligned}$

所以

$\begin{aligned} b_{ij}&=\textbf{z}_i^T\textbf{z}_j\\&= -\frac{1}{2}({}d_{ij}-\frac{1}{N}\sum_{j=1}^{N}d_{ij}-\frac{1}{N}\sum_{i=1}^{N}d_{ij}+\frac{1}{N^2}\sum_{i=1}^{N}\sum_{j=1}^{N}d_{ij}\)\ \end{aligned}$

（6）因为 $\textbf{B}$ 是一个是对称矩阵，因此对矩阵 $\textbf{B}$ 进行特征分解可以得到:

$\textbf{B}=\textbf{V}\Lambda \textbf{V}^T$

其中， $\Lambda$ 是的特征值矩阵， $\textbf{V}$ 是特征向量矩阵。所以

$\textbf{Z}=\textbf{V}{\Lambda}^{\frac{1}{2}}$

5.3非经典MDS的求解方式

当距离标准是欧式距离的时候，可以直接求出解析解。但是当距离标准不是欧式距离的时候，解析解不存在，需要采用优化算法的形式求解。我们的目标是使数据点在高维和低维空间中的距离尽可能的相近，因此我们可以构造如下目标函数（损失函数）:

$J=\frac{1}{N^2}\sum_{i=1}^{N}\sum_{j=i+1}^{N}(||\textbf{z}_i-\textbf{z}_j||-d_{ij})$

通过最小化损失函数的值来求点在 $z$ 维空间的分布。

6.MDS的优缺点

6.1优点：

(1) 不需要先验知识，计算简单

(2) 保留了数据在原始空间的相对关系，可视化效果比较好

6.2缺点:

(1) 如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果

(2) 各个维度的地位相同，无法区分不同维度的重要性。

qq_41267488

关注

3
点赞
踩
15

收藏

觉得还不错? 一键收藏
0
评论
MDS（多维尺度变换）降维算法

1.目标：将目标的（）维表示特征的向量降为（）维，。2.输入数据：，其中为（）维表示第个目标特征的向量，我们将每一个目标看作维空间中的一个点，那么为空间中第个点的坐标。3.输出数据：，其中为（）维表示第个目标降维后的特征向量。4.基本思想将高维坐标中的点投影到低维空间中，保持点彼此之间的相似性尽可能不变。5.方法5.1相似性定义在经典MDS降维算法中，点与点之...
复制链接

扫一扫