Gemini、Kimi 超长上下文秘密，100 万超长上下文如何实现？从 Scaling Law 到超长上下文的大模型优化

Debroon

已于 2025-02-14 11:38:33 修改

阅读量2.5k

点赞数 49

分类专栏：医疗大模型研发 + 慢病逆转文章标签：人工智能算法

于 2025-02-10 16:05:27 首次发布

本文链接：https://blog.csdn.net/qq_41739364/article/details/145542681

版权

医疗大模型研发 + 慢病逆转专栏收录该内容

272 篇文章

订阅专栏

Gemini、Kimi 超长上下文秘密，100 万超长上下文如何实现？从 Scaling Law 到超长上下文的大模型优化

Scaling Law
各个版本的 Scaling Law

超长上下文
基于 GPU 注意力机制优化：标准的自注意力机制 -> Flash Attention 2
使用更强大的 GPU：KV Cache 更大，解码器内的推理神器，加速 QKV 矩阵相乘
优化注意力权重计算方式：MHA（每个头都有 KV） --> MQA（所有头只有一个KV）、GQA（分多组，每组只有一个KV）、MLA（低秩变换优化 KV 权重）
注意力方式：全连接注意力 --> 稀疏注意力
无限注意力【Gemini、Kimi 超长上下文秘密】

位置编码方式：默认的正余弦位置编码 -> ALiBi、RoPE、YaRN 等
RAG + Agent 方式：将长文本结构化为图，Agent 自主探索
改动 MLP 隐藏参数层
使用外部存储来辅助：传统的上下文窗口 -> 外部记忆系统，永久记忆 + 无限上下文
微调实现长上下文

Scaling Law

一、背景分析

近年来，人工智能领域取得了显著进展，尤其是在大规模语言模型（LLM）的训练方面。

OpenAI于2020年提出了“Scaling Law”（缩放定律），揭示了模型性能与模型参数量、训练数据量和计算资源之间的幂律关系。

这一发现为优化模型训练提供了重要指导。

二、核心特征

关键创新点： Scaling Law揭示了模型性能与模型参数量、训练数据量和计算资源之间的幂律关系。
优势： 通过理解Scaling Law，研究人员可以在有限的计算资源下，合理分配模型参数量和数据量，以实现最佳的训练效果。
通俗解释： 就像在烹饪中，食材的种类和数量需要与锅的大小相匹配，才能做出美味的菜肴。同样，模型的参数量和训练数据量需要与计算资源相匹配，才能训练出性能优异的模型。

三、对比理解

正面案例： DeepMind提出的Chinchilla Scaling Law强调，在有限的计算预算下，模型参数量和数据量应均衡增长，以实现最佳性能。这一策略使得模型在性能和计算效率之间取得了良好的平衡。
反面案例： 在早期的模型训练中，研究人员可能过度增加模型参数量，而忽视了数据量的增长，导致模型在训练集上表现良好，但在测试集上泛化能力差。
进步幅度对比： 通过遵循Scaling Law，模型的性能提升呈现幂律关系，即随着计算资源的增加，性能提升逐渐放缓。这意味着，在追求更高性能时，需要投入更多的计算资源。

模型性能、模型大小、数据集大小以及训练计算资源（如计算浮点数）之间存在幂律关系。

随着这三个因素的增加，模型的性能通常会提高，但这些因素的增长是相互依赖的。

当你单独放大某个因素（例如模型大小或数据集大小），如果其他两个因素没有相应增加，模型的性能提升将不会那么显著。

只有当三个因素同时得到充分的放大时，性能才会有显著的提升。

各个版本的 Scaling Law

Scaling Law（缩放定律） 在人工智能领域有多个版本，主要由不同的研究团队提出，针对模型规模、训练数据量和计算资源之间的关系进行了深入分析。

1. OpenAI的Scaling Law（2020年）

OpenAI在2020年提出的Scaling Law，研究了模型参数量（N）、训练数据量（D）和计算量（C）之间的关系。

他们发现，测试损失（L）与模型参数量和训练数据量的关系可以表示为：

$L_0 + \left( \frac{C_0}{C} \right)^\alpha$

其中，( L_0 ) 是理想生成过程的损失，( C_0 ) 是常数， $\alpha$ 是与模型架构相关的指数。他们的研究表明，随着计算量的增加，模型的测试损失呈现递减趋势，但收益递减。

2. DeepMind的Chinchilla Scaling Law（2022年）

DeepMind在2022年提出了Chinchilla Scaling Law，强调在有限的计算预算下，模型参数量和训练数据量应均衡增长，以实现最佳性能。

他们的研究发现，计算量（C）、模型参数量（N）和训练数据量（D）之间的关系为：

$C_0 \times N \times D ]$
$\frac{A}{N^\alpha} + \frac{B}{D^\beta} + L_0 ]$

其中，( C_0 ) 是常数，( A )、( B )、 $\alpha$ 和 $\beta$ 是与模型架构和数据集相关的参数。

他们的研究强调，增加训练数据量对于提升模型性能至关重要。

$\frac{A}{N^{0.34}} + \frac{B}{D^{0.28}}$

其中：

L 代表模型的测试损失值(test loss)
N 是模型的参数量
D 是训练数据的token数量
$\approx 1.69$ (基准常数)
$\approx 406.4$ (参数相关系数)
$\approx 410.7$ (数据相关系数)

以 Qwen2-7B 的 7B 参数， 15T 训练集为例子：

$\times 10^9, 15 \times 10^{12}) = 1.86$

模型性能与参数量N的关系是-0.34次幂

模型性能与数据量D的关系是-0.28次幂

这表明增加参数量和数据量都会带来性能提升，但都存在边际递减效应.

如果已知模型的参数量和目标性能，可以通过Scaling Law公式反推出所需的tokens数量

在这里插入图片描述

3. 其他研究

除了OpenAI和DeepMind的研究外，还有其他研究团队对Scaling Law进行了探索。

例如，2024年4月，Tamay Besiroglu等人对Chinchilla Scaling进行了复制实验，发现其参数与原始研究略有差异，提出了新的参数估计值。

对比分析

模型参数量与训练数据量的关系： OpenAI的Scaling Law强调计算量与模型参数量和训练数据量的关系，而DeepMind的Chinchilla Scaling Law则强调模型参数量和训练数据量的均衡增长。
计算量的影响： OpenAI的研究表明，随着计算量的增加，模型的测试损失递减，但收益递减。DeepMind的研究则强调，在有限的计算预算下，如何合理分配计算资源以实现最佳性能。
数据量的重要性： DeepMind的研究强调，增加训练数据量对于提升模型性能至关重要。

OpenAI的Scaling Law适用于计算资源丰富的情况，强调计算量的增加对性能的影响；

而DeepMind的Chinchilla Scaling Law则适用于计算资源有限的情况，强调模型参数量和训练数据量的均衡增长。

超长上下文

基于 GPU 注意力机制优化：标准的自注意力机制 -> Flash Attention 2

论文：【大模型上下文长度扩展】FlashAttention：高效注意力计算的新纪元、【大模型上下文长度扩展】FlashAttention-2：比1代加速1.29倍、GPU利用率从55%上升到72%

Flash Attention 是一种基于 GPU 的优化注意力机制，旨在解决传统注意力机制（如 Transformer 中的自注意力机制）在处理大规模数据时的计算瓶颈。

传统的自注意力机制在进行矩阵乘法时，由于 O(n²) 的复杂度和内存需求，处理长序列时会变得极其缓慢且内存占用过高。

Flash Attention 的设计目标是通过更高效的计算和内存管理来缓解这一问题，尤其在基于 GPU 的加速计算中具有显著优势。

GPU 有 2 部件：

HBM 是主存储器，用于存放大规模数据集（如深度神经网络中的权重、激活等）。
SRAM 是 GPU 的一级缓存（L1 cache）和二级缓存（L2 cache）的基础，它存储计算过程中非常频繁访问的数据，例如某些局部计算结果或重要的计算参数，其速度非常快。
同样的计算，SRAM 比 HBM 快 20 倍，那把一些计算放到 SRAM 就能提升计算速度。

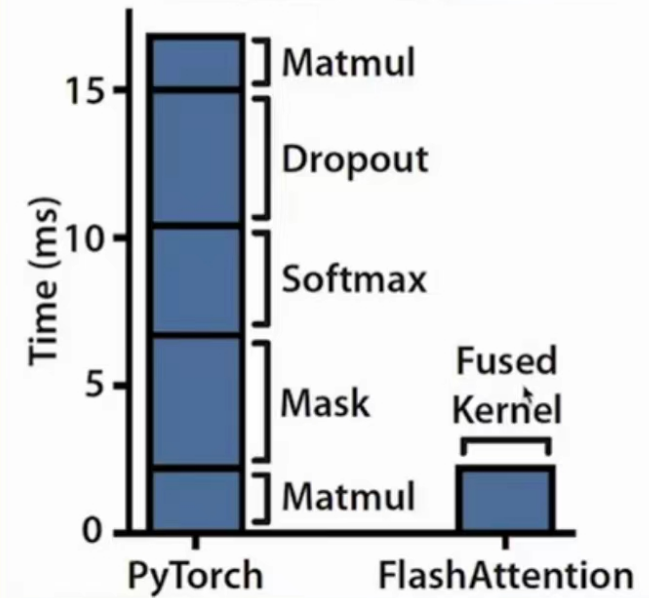
在这里插入图片描述

传统自注意力机制：矩阵相乘 + 掩码 + softmax百分比 + Dropout泛化 + 矩阵相乘。

其实大头的时间，矩阵相乘只有一小部分，掩码和Dropout泛化占大头。

Flash Attention：把其中耗时的计算，移动到 SRAM 计算。

在传统的注意力计算中，注意力矩阵需要被完全存储。

Flash Attention 通过 分块计算 将大矩阵分成更小的子块（小矩阵），每次只计算一个小块的内容。

这样做的好处是，当计算一个小块时，计算所需要的数据可以更容易地存储在 GPU 的高速缓存（比如 SRAM，计算速度提高 20 倍）中，而不必每次都从内存中读取整个大矩阵。

第二步，将每个子块的计算任务并行执行，使得 GPU 的多个计算核心能够同时处理多个子块的计算任务。

第三步，在线的 softmax

CPU 是一个博士（微积分都会，但只有一个人），GPU 是一群小学生（虽然只会加减乘除，但特别适合这种并行）。

特性	传统注意力机制	Flash Attention
计算复杂度	$(O(n^2 \cdot d))$	更优化的内存和计算方法，复杂度降低
内存占用	高，尤其是长序列时，内存需求急剧增加	通过分块和优化内存访问，减少内存占用
计算效率	较低，尤其在处理长序列时性能瓶颈明显	高效，充分利用 GPU Tensor Cores 提升计算速度
GPU 利用	未完全优化，无法充分利用 Tensor Cores	高效利用 GPU，支持低精度计算
并行化	一定程度的并行化，但存在计算瓶颈	更强的并行化能力，减少冗余计算
适用场景	适用于短序列和较小规模的模型	适用于长序列、大规模模型，尤其在大数据集下表现突出

使用更强大的 GPU：KV Cache 更大，解码器内的推理神器，加速 QKV 矩阵相乘

KV Cache 是指 键（Key） 和 值（Value） 缓存，用于加速自注意力机制（例如 Transformer 中的注意力计算）中的计算过程。

它在 自注意力计算 中特别有用，尤其是在进行 推理（inference） 时，可以显著提高效率，减少重复计算。

在推理过程中（特别是 生成式任务 如文本生成、机器翻译等），输入序列通常是逐步生成的，模型每次生成一个新的词或标记时，需要基于前面的结果进行计算。这时，KV Cache 的作用尤为重要。

KV Cache 是将 键（Key） 和 值（Value） 缓存起来，以便在推理过程中不需要每次都重新计算这些值。

尤其在 生成任务 中，随着每一步生成新单词时，模型只需要计算新的查询（Query）与之前存储的键（Key）和值（Value）进行交互，而不必从头开始计算整个注意力矩阵。

如何工作：

在生成过程中，模型会逐步生成输出。例如，在文本生成中，模型从第一个单词开始，计算它与序列中其他单词的相关性，然后生成下一个单词。
在每生成一个新的单词后，模型会将生成的 键（Key） 和 值（Value） 缓存起来。
当生成下一个单词时，模型将不需要重新计算整个输入序列的键和值，而是直接使用缓存的 键（Key） 和 值（Value）。

这种缓存机制可以显著 减少计算量，避免了每次都重新计算每个单词的键和值，尤其是当输入序列很长时，KV Cache 极大地加速了推理过程。

KV Cache 的好处：

加速推理过程：每次生成一个新单词时，只需要基于当前输入与缓存的键值进行计算，避免了从头开始计算的重复工作。
节省内存：因为缓存只存储键和值，而不需要存储整个注意力矩阵，这有效地减少了内存需求。
提高效率：KV Cache 能够加速序列生成过程，尤其在大型生成模型中，显著减少了延迟。

假设我们要生成一个句子 “The cat is on the mat”：

初始时：模型输入 “The” 后，计算其对应的键（Key）和值（Value），并将它们存入缓存。
生成下一个单词：模型根据缓存的键和值生成 “cat”。
继续生成：当生成 “is” 时，模型只需要计算查询（Query）与之前的键（Key）和值（Value）进行交互，而不需要重新计算 “The” 和 “cat” 的键和值，使用缓存中的键值即可。

通过这种方式，随着序列长度的增加，模型的计算量不会像传统的全序列计算那样指数增长，而是线性增加，从而提高生成效率。

KV Cache 是在自注意力机制中，用于存储已经计算过的 键（Key） 和 值（Value） 的缓存。

它使得在推理过程中，生成模型能够在每一步的计算中重复利用先前的计算结果，而不需要重新计算整个输入序列的注意力矩阵，从而加速计算和减少内存占用。

想象你在做一道复杂的菜肴，而每个步骤都需要用到一些配料。每次做饭时，你需要从冰箱里拿出很多配料（如肉、蔬菜等），然后开始处理这些配料。

但有些配料是重复使用的（如盐不够，可能要加几次），比如你需要多次用到相同的调料或者食材。

传统做饭过程（没有 KV Cache）

每次做饭时，你都需要重新从冰箱里取出所有的配料，再按照食谱逐步准备。
如果你在做菜的过程中需要重复使用某些食材，每次都要从冰箱重新取出来，这样就浪费了时间和精力。

使用 KV Cache（优化后的做饭过程）

假设你在做饭时将一些常用的配料（比如常用的调料、已经切好的蔬菜）放在一个小篮子里，这个篮子就是你 KV Cache。
这样，当你需要再用这些食材时，你不需要每次都去冰箱里重新拿，而是直接从篮子里取出，省时省力。

类比与 KV Cache 的关系：

冰箱里的配料：就像是 键（Key） 和 值（Value）。这些配料是你做饭时需要的食材，代表着自注意力中的输入信息。
篮子（KV Cache）：是一个临时存放已准备好的食材的地方，它缓存了你已经处理过的配料（即已经计算过的键和值）。每次你做饭时，可以直接从篮子里拿，而不需要重新从冰箱里取出。
做饭过程：类似于模型生成的每一步。在生成的每个新单词时，模型不需要重新计算所有的键和值，而是直接利用之前计算过的结果（缓存的键和值）。

就像你做饭时如果把常用的配料放在篮子里，可以重复利用它们，KV Cache 在模型推理过程中缓存了已经计算过的键和值。

这样模型在每次生成新的输出时，不需要重新计算之前已经做过的工作，从而提高效率和减少计算负担。

优化注意力权重计算方式：MHA（每个头都有 KV） --> MQA（所有头只有一个KV）、GQA（分多组，每组只有一个KV）、MLA（低秩变换优化 KV 权重）

在这里插入图片描述
MHA 占有的 KA Cache 太多，如上图。

MHA (Multi-Head Attention)
多头注意力（MHA） 是 Transformer 中自注意力机制的核心组成部分，广泛应用于自然语言处理（NLP）任务中。

工作原理：

查询（Query）、键（Key）、值（Value）：MHA 和传统的自注意力机制一样，首先将输入分为查询、键和值三个部分。
多个头（Heads）：MHA 的核心思想是使用多个“头”来并行地计算注意力。每个头都在不同的子空间中进行注意力计算，最后将这些头的输出合并。每个头在计算注意力时，使用不同的参数矩阵（不同的权重），通过这种方式可以从多个角度学习不同的特征。
合并输出：多个头的结果会通过拼接或加权平均的方式进行合并，并映射到输出空间。

优势：

捕获多样性：每个头可以关注输入数据的不同部分，从不同的角度理解数据，因此多头注意力可以捕获更加丰富的表示。
并行性：多个头可以并行计算，提高计算效率。

应用场景：

主要用于 Transformer 模型中，广泛应用于 NLP（如机器翻译、文本生成、问答等）和 计算机视觉（如图像描述生成、图像分类等）。

MQA (Multi-Query Attention)
多查询注意力（MQA） 是对 MHA 的一个优化变种，旨在减少计算复杂度，特别是在生成式任务中。

工作原理：

在标准的多头注意力中，查询（Query）、键（Key）和值（Value）都是来自输入序列中的每个元素（或者嵌入的表示）。而在 MQA 中，模型使用多个查询（Queries）来与共享的键和值进行交互。
具体来说，多个查询 会共享同一组键和值进行计算，而不是像传统的 MHA 那样，针对每个查询都计算不同的键和值。这样做可以大大减少计算量，特别是在查询数量远大于输入序列长度时。

优势：

减少计算复杂度：由于多个查询共享相同的键和值，可以减少计算量，特别是在需要同时处理多个查询的场景下（如批量推理）。
提高计算效率：尤其在生成任务（如对话系统、文本生成等）中，能够加速推理过程。

应用场景：

适用于 生成任务 和 推理任务，特别是在每次生成多个输出（例如生成多个候选文本或生成多个翻译时），常见于 对话系统、机器翻译、文本生成等领域。

但学习语义深度、丰富度是不如 MHA 的，因为都变成 1 个了。

然后就诞生了中间的平衡方案，保证学习深度和丰富的同时，还要减少计算量。

GQA (Generalized Query Attention)
广义查询注意力（GQA） 是一个更广泛的注意力机制，旨在通过优化查询、键和值的交互方式，使得注意力机制更加灵活和通用。GQA 不是一个特定的模型，而是一个通用的框架，能够适应多种不同类型的任务。

工作原理：

灵活的查询机制：GQA 允许查询、键和值之间有更加灵活的交互方式。与标准的 MHA 和 MQA 相比，GQA 的查询、键和值可以来自不同的数据源，或者根据任务需求进行定制。
多模态输入：GQA 设计允许来自多个模态的数据进行交互（如文本、图像、音频等），可以处理更复杂的任务。
任务自适应：GQA 允许根据不同任务的需求调整查询的处理方式，能够在不同的应用场景中自适应优化注意力机制的表现。

优势：

通用性强：GQA 能够适应不同的任务，不仅限于自然语言处理任务，还可以扩展到多模态学习（如视觉-语言模型）。
灵活性：能够根据任务需求灵活地调整查询、键和值之间的交互方式，提高任务的执行效率和效果。

应用场景：

多模态任务（如视觉-语言任务）：GQA 可以同时处理文本和图像的联合表示，用于图像描述生成、视觉问答（VQA）等任务。
跨模态任务：例如在处理文本和图像输入时，GQA 可以将两者的信息融合，从而提高模型对多模态输入的理解和处理能力。
适用于需要 灵活查询机制 的任务，比如 多任务学习 或 跨模态推理。

MLA 结合了低秩投影和共享 KV 权重的想法，它的关键点在于如何在保持性能的同时，显著减少内存和计算开销：

低秩投影：在 MLA 中，模型通过低秩矩阵对查询（Q）、键（K）和值（V）进行降秩变换，利用较少的参数来学习关键特征，从而减少了模型的内存消耗和计算复杂度。类似于 LoRA，低秩投影帮助模型在处理新任务时，仅优化少量参数。
私有和公用KV权重：MLA 将公用的 KV 权重 和私有的 KV 权重 分离。公用的 KV 权重可用于多个查询（如 MHA 中），而私有的 KV 权重被藏在 Q 和 V 的投影矩阵中，减少了缓存所需存储的内存量。
位置编码：MLA 采用类似于 RoPE 的方法，通过扩展 Q 和 K 的维度来处理位置编码，避免了位置编码增加缓存需求，从而进一步减少内存消耗。

MLA 通过 低秩投影 和 共享 KV 权重 等技术，在保留模型表现的前提下，显著提高了内存和计算效率，适合处理大规模、长序列的任务。

MHA、MQA 和 GQA 、MLA 对比

特性	MHA (Multi-Head Attention)	MQA (Multi-Query Attention)	GQA (Generalized Query Attention)	MLA (Multi-head Latent Attention)
基本概念	多个并行的注意力头，每个头独立计算注意力	多个查询共享相同的键和值，减少计算复杂度	灵活的查询和键值交互方式，支持多模态输入	将公共和私有的KV权重分离，进行低秩线性变换，节省内存
计算方式	每个头独立计算，通过拼接合并输出	多个查询共享同一组键和值，减少计算量和内存消耗	允许查询、键和值之间更灵活的交互，适应不同任务需求	使用低秩投影矩阵进行线性变换，实现降秩操作，减少内存需求
低秩矩阵应用	没有低秩矩阵优化	间接通过共享键和值，减少计算复杂度	通过调整查询和键值的交互方式，适应任务需求	使用低秩矩阵（如LoRA），将公共和私有的KV权重矩阵降秩
优化目标	提高表示学习的多样性，增强模型的表达能力	降低计算复杂度，特别是在生成任务和批量推理时	提供更高的灵活性和通用性，适应多模态和多任务学习	通过降秩投影优化内存使用，减少计算复杂度和训练阶段的参数量
应用场景	主要用于 NLP 和计算机视觉（如 Transformer、BERT 等）	适用于生成任务、对话系统、机器翻译、文本生成等	多模态任务、视觉-语言任务、跨模态推理、任务自适应场景	用于高效的生成任务，特别是在处理长序列时节省内存，优化推理速度
权重矩阵的形状变化	原始权重矩阵，多个注意力头并行计算	缩小KV矩阵大小，多个查询共享键和值	权重矩阵通过线性变换降低秩，适应任务需求	公共和私有KV权重通过低秩投影矩阵处理，减小内存占用
私有与公用KV权重的处理	每个头有独立的KV权重	多个查询共享KV权重	不同的任务和输入共享查询、键和值	私有KV权重投影到Q和V中，公用KV共享，减少内存占用
内存效率	计算量和内存需求较高	减少计算和内存需求，特别是在生成任务中	适应不同任务的需求，灵活调整内存使用	通过低秩投影和KV共享显著节省内存，特别适合大规模任务
位置编码	位置编码直接应用于Q和K	对位置编码的处理与MHA相似	灵活处理位置编码，允许跨模态任务	通过Q和K的维度扩展来处理位置编码，减少缓存需求
推理加速	计算量较大，推理过程较慢	通过共享KV权重提高推理效率	灵活的查询处理加速推理，尤其是跨模态任务	通过低秩投影矩阵减少推理过程中的计算负担和内存消耗
优点	捕获不同的信息，增强模型的表达能力	高效计算多个查询，减少计算开销	更加通用和灵活，适应多种任务和输入类型	降低内存占用和计算复杂度，通过低秩投影和共享 KV 权重提高效率，同时保持性能

注意力方式：全连接注意力 --> 稀疏注意力

注意力机制的本质是通过加权聚合输入的不同部分来自动决定哪些部分在当前任务中更重要，从而提高模型对关键信息的关注度。

它使得模型能够在处理数据时，灵活地选择和集中在最相关的信息上，而不是平等对待所有信息。

在这里插入图片描述

Full Attention (完整注意力)

在左上角，展示的是 Full Attention（完全注意力），即在传统的自注意力机制中，所有输入的元素（如词语）都会与其他所有元素进行交互。
这是一个 全连接 的图，意味着每个节点（如词语）与每个其他节点都有边连接，计算量非常大，特别是在处理长序列时会导致计算和内存的巨大消耗。
矩阵表示：在矩阵中，每个元素都与其它所有元素连接，因此形成一个密集矩阵，复杂度为 $O(n^2)$ ，其中 (n) 是序列长度。

自注意力机制就是完整注意力机制的一种：

在这里插入图片描述
在处理一个元素时考虑到序列中其他元素的信息。

掩码 + 自注意力：

在掩码自注意力中，掩码被用来确保模型在生成一个元素的表示时，只能看到当前或之前的元素，而不能看到未来的信息。

比如是，只能看到你。

稀疏注意力（Sparse Attention）

稀疏注意力机制尝试通过减少计算和内存消耗，避免全连接的计算，使用不同的稀疏模式（随机、相邻、全局）来进行优化。

图的下部分展示了三种稀疏模式，它们分别是：

Random (随机连接)：
- 在这个模式下，注意力矩阵中的部分位置是随机连接的，而不是与所有元素都有连接。
- 这种方法减少了计算量，但仍然保持了一些随机的全局依赖关系。
- 矩阵表示：稀疏的随机连接形式是矩阵中某些位置的元素为非零值，其他位置为零。它可以显著减少计算量。
Window (窗口连接)：
- 窗口模式将注意力局限在一个固定大小的窗口内，只计算相邻位置的关系。
- 这种方法非常适合处理局部依赖的任务，比如在语言建模中，许多词语与周围词语的关系更为紧密。
- 矩阵表示：窗口中的元素是连续的非零元素，其他区域为零，从而减少了计算范围。
Global (全局连接)：
- 全局模式表示对某些特定位置（如某些关键字或特殊标记）保持全连接，而其他部分保持稀疏。
- 这种方法允许模型对重要的全局信息（如段落的开头或特殊的标记）有较强的感知能力，同时保持其他部分的稀疏性。
- 矩阵表示：矩阵中会有部分全局连接的区域，其他位置则为零。

BigBird (结合多种稀疏模式)

BigBird 是结合了上述三种稀疏模式（随机连接、窗口连接和全局连接）的一种方法，它利用这些不同的稀疏模式来减少计算量并提高效率，同时保持较高的模型性能。
- BigBird的连接：BigBird 在矩阵中混合了随机、窗口和全局连接。这样，它既能捕捉到局部依赖，也能通过随机连接和全局连接来保持长距离依赖的表达。
优势：这种结合多种稀疏模式的方法大大降低了计算复杂度，尤其是在长序列的处理上。通过将全连接转换为稀疏连接，BigBird 显著减少了计算和内存开销，但仍然能够捕捉全局信息。

在这里插入图片描述

无限注意力【Gemini、Kimi 超长上下文秘密】

无限注意力论文：Leave No Context Behind: Efficient Infinite Context Transformers with Infini-attention

经过测试，谷歌 100 万超长上下文，有 40% 的信息丢失。

因为算法处理核心逻辑是：压缩记忆 + 局部与长时线性提取。

假设我们有一段非常长的文本，长度超过了传统Transformer模型的最大上下文长度（例如1M个token）。

传统的Transformer模型会将超过最大上下文长度的部分丢弃，导致丢失重要的信息。

使用 Infini-attention 机制时，模型并不会丢弃旧的上下文，而是将之前处理过的输入（例如之前的token的key-value对）存储在压缩记忆中。

当处理新的输入时，模型会通过查询（query）来从压缩记忆中检索到旧的信息，并将这些信息与当前输入的局部上下文结合，生成最终的输出。

假设你正在阅读一本书，书的内容有一百万个字。

在传统模型中，如果你只看到前两千个字，模型就无法“记住”后面的内容。

而使用 Infini-attention 时，模型能够通过压缩记忆保存之前的内容，并在读取新章节时不断“回忆”这些内容，从而理解整个书的情节，即使输入的长度非常长。

谷歌论文中的Infini-attention机制也涉及了类似的压缩记忆和长距离信息提取的方式。

谷歌的线性提取，参考论文：

线性提取论文：Efficient Attention: Attention with Linear Complexities

首先计算 $K^T V)$ 得到一个合成的全局上下文向量（即“模板”），然后通过查询矩阵 (Q) 对这些模板进行加权，得到最终的输出。

这样，信息的提取不再依赖于每个位置之间的直接计算，而是通过已聚合的全局上下文（模板）进行查询。

在这里插入图片描述

原来计算：【Q * K 大矩阵】 x 【V】。

Q[4096, 512] * K[512, 4096] = Q*K[4096 * 4096] 维【俩俩文字间特征值加权和，计算每个位置之间的相似度】 x V[4096, 512] = [4096, 512]

现在计算：【K * V 相当于做了一个总结，变成一个超小矩阵】 x 【Q】。

K[512, 4096] * V[4096, 512] = K*V[512, 512] 维【过去所有文字每个特征值的总和，对所有历史文字的压缩总结】 x Q[4096, 512] = [4096, 512]

位置编码方式：默认的正余弦位置编码 -> ALiBi、RoPE、YaRN 等

预训练使用小窗口训练（如 4k 上下文），微调阶段使用大窗口（如 50 k 上下文） + 长上下文的位置编码方式（相对位置编码）。

正余弦位置编码属于绝对位置编码。

通过使用正弦和余弦函数为每个位置生成一个独特的向量，表示输入序列中元素的绝对位置。

这些位置向量会与输入的词向量相加，从而将位置信息融入到模型中。

绝对位置编码关注的是每个元素在序列中的固定位置，而不考虑元素之间的相对关系。

相对位置编码则是关注元素之间的相对距离。

在这里插入图片描述

相对位置编码 — 能学习文字间的相对信息，但是无法使用 KV Cache。

【大模型上下文长度扩展】线性偏差注意力 ALiBi

【大模型上下文长度扩展】RoFormer：一种结合了旋转位置编码（RoPE）的Transformer模型

【大模型上下文长度扩展】YaRN：旋转位置编码，以文匹意，精细化衔接长篇

【大模型上下文长度扩展】位置内插 PI：基于Positional Interpolation扩大模型的上下文窗口

比如正余弦位置编码和 RoPE。

相同点：

两者的目标都是为Transformer模型提供位置信息，以便模型能够理解序列中元素的相对位置。
两者都基于正弦和余弦函数生成位置编码，都利用周期性函数来表达不同位置的编码。

差异：

正余弦位置编码：为每个位置生成一个固定的编码向量，这些向量通过正弦和余弦函数与不同频率的参数计算。
RoPE的基本思想是将位置编码与词向量通过旋转操作结合，而不是直接相加。它通过在每个维度上应用旋转（通过正余弦函数）来为每对词之间的关系提供动态的相对位置编码。这种方法能够更自然地表示长距离依赖。

正余弦位置编码：就像 地图上的固定坐标。地图上标记了每个地点的绝对位置，每个地点都有一个明确的坐标，但地图本身并不动态改变，它只提供静态的地理位置。

RoPE (Rotary Position Encoding)：类似于 使用指南针定位。指南针不仅告诉你当前位置，还能指引你如何根据当前方位旋转和移动，帮助你了解不同地点之间的相对方位和距离。RoPE通过旋转来动态调整词语之间的相对位置，使得模型能够捕捉到更细腻的相对依赖关系。

绝对位置编码相当于一条直线，因为它通过为每个位置生成固定的编码，并直接将其加到词向量中，表现为每个位置的绝对坐标信息。这种编码是静态的，位置和词的关系通过一个固定的、线性顺序来表示。

RoPE (Rotary Position Encoding) 相当于一条螺旋线，因为它通过旋转操作将位置编码动态地应用到词向量中，类似于沿着一个三维空间的螺旋路径旋转。RoPE不仅考虑了词的绝对位置，还根据相对位置关系进行旋转，这样在长序列中，词之间的相对距离和依赖关系能够通过旋转的方式进行动态表达，捕捉到更复杂的相对关系。

YaRN（动态曲线）：YaRN 在 PI、NTK 基础上，对 RoPE 扩展，会涉及多维旋转或更多动态的调整，因此它可以视为在更复杂的、非线性的曲线空间中进行位置编码。

总结来说，YaRN 比 RoPE 更加灵活和复杂（Qwen、Llama 采用 YaRN），涉及多维度的旋转或变换，因此它可以类比为在 更复杂的曲线 中表示位置编码，旨在更有效地处理序列中的复杂依赖关系。