数据结构PTA 案例6-1.3 哥尼斯堡的“七桥问题”

题目

哥尼斯堡是位于普累格河上的一座城市，它包含两个岛屿及连接它们的七座桥，如下图所示。

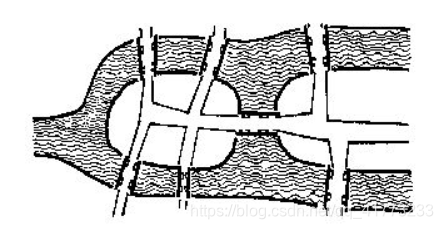
可否走过这样的七座桥，而且每桥只走过一次？瑞士数学家欧拉(Leonhard Euler，1707—1783)最终解决了这个问题，并由此创立了拓扑学。

这个问题如今可以描述为判断欧拉回路是否存在的问题。欧拉回路是指不令笔离开纸面，可画过图中每条边仅一次，且可以回到起点的一条回路。现给定一个无向图，问是否存在欧拉回路？

输入格式:
输入第一行给出两个正整数，分别是节点数N (1≤N≤1000)和边数M；随后的M行对应M条边，每行给出一对正整数，分别是该条边直接连通的两个节点的编号（节点从1到N编号）。

输出格式:
若欧拉回路存在则输出1，否则输出0。

输入样例1:

6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6

输出样例1:

1

输入样例2:

5 8
1 2
1 3
2 3
2 4
2 5
5 3
5 4
3 4

输出样例2:

0

解法

思路
如果一个图需要满足以下两个条件，那么欧拉回路必存在，任意一个不满足，则不存在。（当然这是充要条件）

1. 每个顶点的度为偶数
2. 图是连通的

要想判断条件一，可以给图的类型中加一个Data数组，用来记录每个顶点的度，这个记录过程可以放在插入边InsertEdge函数中进行。
要想判断条件二，可以用深度遍历，只要从任意一点出发遍历后，每个顶点都访问到，那么图就是连通的。

因此这是一道简单的图的问题。注意在文本的实现中，Graph->G, Graph->Data, Visited都是动态数组，这样不浪费空间。

实现

#include<stdio.h>
#include<stdlib.h>

#define INFINITY 100000
#define MAXN 1000

typedef int Vertex;
typedef int WeightType;
typedef int DataType;

typedef struct GNode *PtrToGNode;
typedef PtrToGNode MGraph;
struct GNode
{
    int Nv;
    int Ne;
    WeightType **G;
    DataType *Data;     //calculate the degree of vertex
};

typedef struct ENode *PtrToENode;
typedef PtrToENode Edge;
struct ENode
{
    Vertex V1, V2;
    WeightType W;
};

MGraph CreateGraph(int VertexNum)
{
    int i,j;
    MGraph Graph = (MGraph)malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->G = (WeightType **)malloc(Graph->Nv*sizeof(WeightType *));
    for(i=0; i<Graph->Nv; i++)
    {
        Graph->G[i] = (WeightType*)malloc(Graph->Nv*sizeof(WeightType));
    }

    for(i=0; i<Graph->Nv; i++)
    {
        for(j=0; j<Graph->Nv; j++)
            Graph->G[i][j] = INFINITY;
    }

    Graph->Data = (DataType *)malloc(Graph->Nv*sizeof(DataType));
    for(i=0; i<Graph->Nv; i++)
        Graph->Data[i] = 0;

    return Graph;
}

void InsertEdge(MGraph Graph, Edge E)
{
    Graph->G[E->V1][E->V2] = E->W;
    Graph->G[E->V2][E->V1] = E->W;
    Graph->Data[E->V1]++;
    Graph->Data[E->V2]++;
}

MGraph BuildGraph()
{
    int i,N,M;
    scanf("%d %d", &N, &M);
    MGraph Graph = CreateGraph(N);
    Graph->Ne = M;

    if(Graph->Ne != 0)
    {
        Edge E = (Edge)malloc(sizeof(struct ENode));
        for(i=0; i<Graph->Ne; i++)
        {
            scanf("%d %d", &E->V1, &E->V2);
            E->V1--;
            E->V2--;
            E->W = 1;
            InsertEdge(Graph, E);
        }
    }

    return Graph;

}



int *Visited;

void DFS(MGraph Graph, Vertex V)
{
    Visited[V] = 1;
    int i;
    for(i=0; i<Graph->Nv; i++)
    {
        if(Graph->G[V][i] == 1 && Visited[i] == 0)     //V is adjacent to i, and i is not visited
        {
            DFS(Graph, i);
        }
    }
}


int main()
{
    int i;
    MGraph Graph = BuildGraph();
    Visited = (int *)malloc(Graph->Nv*sizeof(int));
    for(i=0; i<Graph->Nv; i++)
        Visited[i] = 0;
    
    
    DFS(Graph, 0);
    int flag;
    flag = 1;
    for(i=0; i<Graph->Nv; i++)
    {
        if(Visited[i] == 0 || Graph->Data[i]==0 || Graph->Data[i]%2 != 0)
        {
            flag = 0;
            break;
        }

    }
    printf("%d", flag);

    return 0;
}