对于微积分的核心概念,个人感觉有一句话描述的非常到位,"导数是变化的原因,积分是变化的结果"!
书上对微积分基本定理的描述以及证明如下:
设  在闭区间
在闭区间![[a,b]](https://i-blog.csdnimg.cn/blog_migrate/4a3fed74916c2fcfdc496b1a7bdcf662.gif) 上连续,
上连续,  是
是 在
在![[a,b]](https://i-blog.csdnimg.cn/blog_migrate/4a3fed74916c2fcfdc496b1a7bdcf662.gif) 上的一个原函数,则:
上的一个原函数,则:

给出的证明过程是:
因 与
与
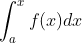
均是 在
在![[a,b]](https://i-blog.csdnimg.cn/blog_migrate/4a3fed74916c2fcfdc496b1a7bdcf662.gif) 上的原函数,只能相差一个常数,即:
上的原函数,只能相差一个常数,即:
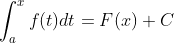
让
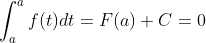
所以
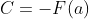
则:
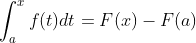
令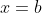
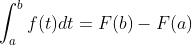
得证。
这个证明比较突兀,尤其是
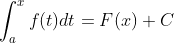 ,一笔带过,很是气人,究竟为什么函数的积分和它的原函数之间有此种联系呢?并未说明,下面用数形结合的方式尝试说明这个问题。
,一笔带过,很是气人,究竟为什么函数的积分和它的原函数之间有此种联系呢?并未说明,下面用数形结合的方式尝试说明这个问题。
首先,插入一个只要介绍微积分必会用来做例子的经典题目,求方程

在闭区间![[0,1]](https://i-blog.csdnimg.cn/blog_migrate/3943a1ea6262eda3459ef08fb65c48fa.gif) 上的面积。
上的面积。

经典做法是,上图绘制每个区域都选择这个区域的最大速度,这种取法叫做上和,还也可以取下和,就是每个区的最小速度,甚至是中和,都没有关系,根据夹逼定理,无论哪种取法,当n趋进于 时都是一样的,
时都是一样的,
将区间![[0,1]](https://i-blog.csdnimg.cn/blog_migrate/3943a1ea6262eda3459ef08fb65c48fa.gif) 平均分成n等份,每一份的长度是
平均分成n等份,每一份的长度是 ,那么面积S等于:
,那么面积S等于:
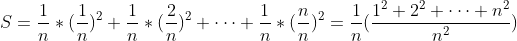
这个和有一个专门的名字,叫做黎曼和,它的通用形式是:
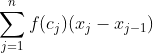
这里
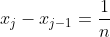
其中根据平方和公式:
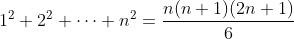
所以
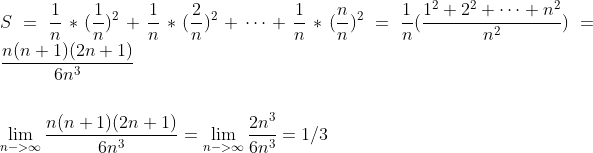
这个结果和通过微积分基本定理得到的结果是一致的。
接下来我们用上图一样的原来来证明微积分基本定理:
第一步,联接函数图形上n个分点相邻点,我们可以用这条线段的斜率作为导函数的近似。

设从原点开始的每个线段的为
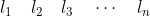
则
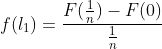
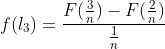






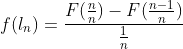
那么,由于
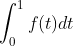
可以表示成函数曲线和坐标轴以及定义域围城的图形的面积,也就是:
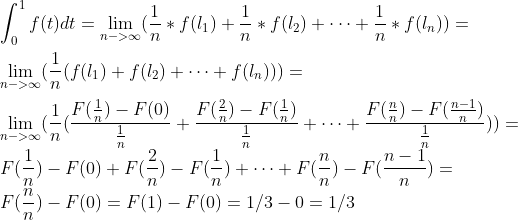
我们也可以进行一下代数推导,如下图所示:
 '
'
设:
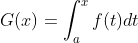
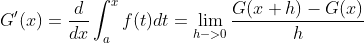
其中:
就是上图中阴影部分的面积(包括顶部弯的部分).
当h很小的时候,可以用阴影矩形区域替代.

所以
 是f(x)的原函数.
是f(x)的原函数.
得证!
图形化说明:

geogebra说明

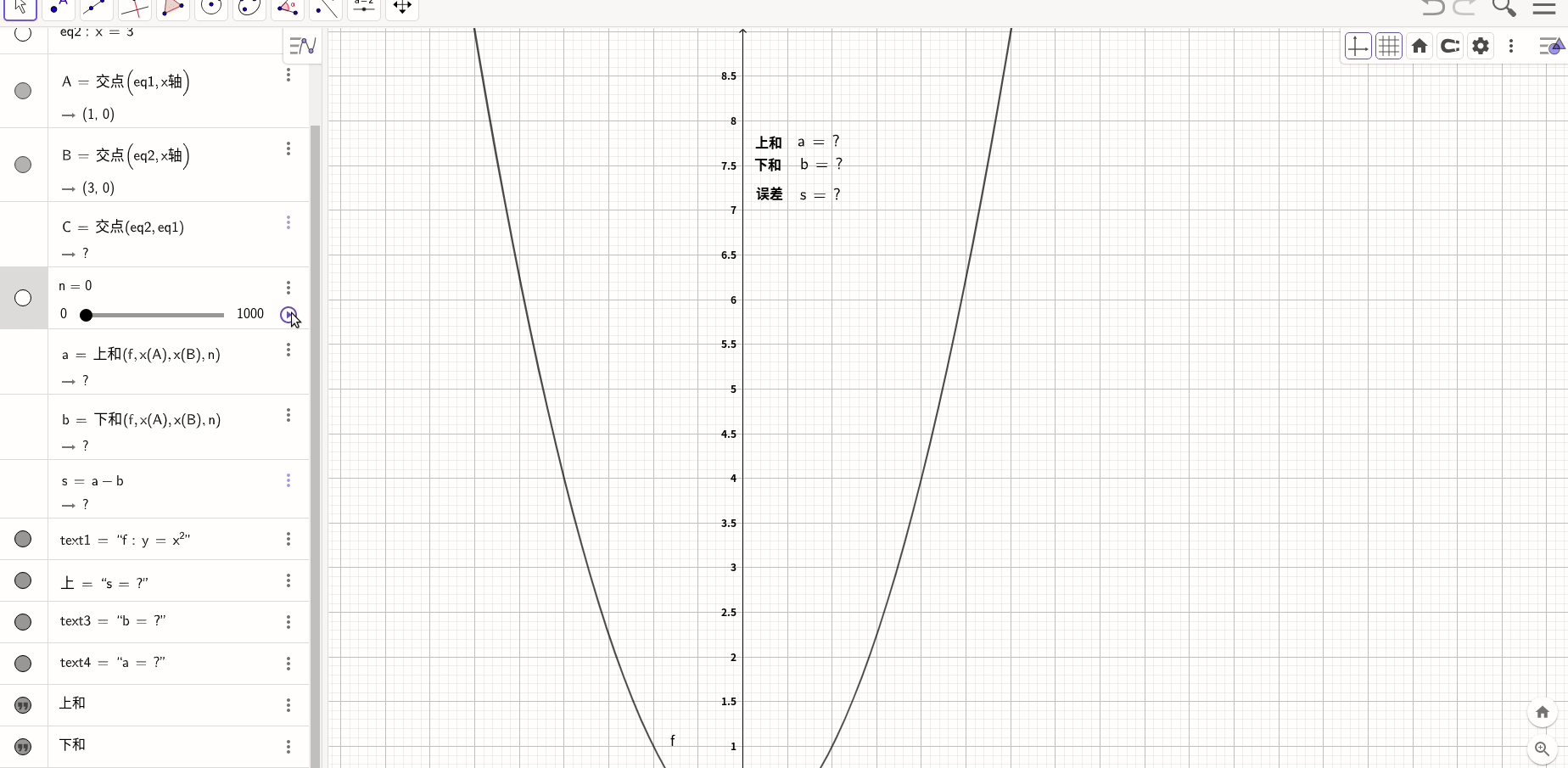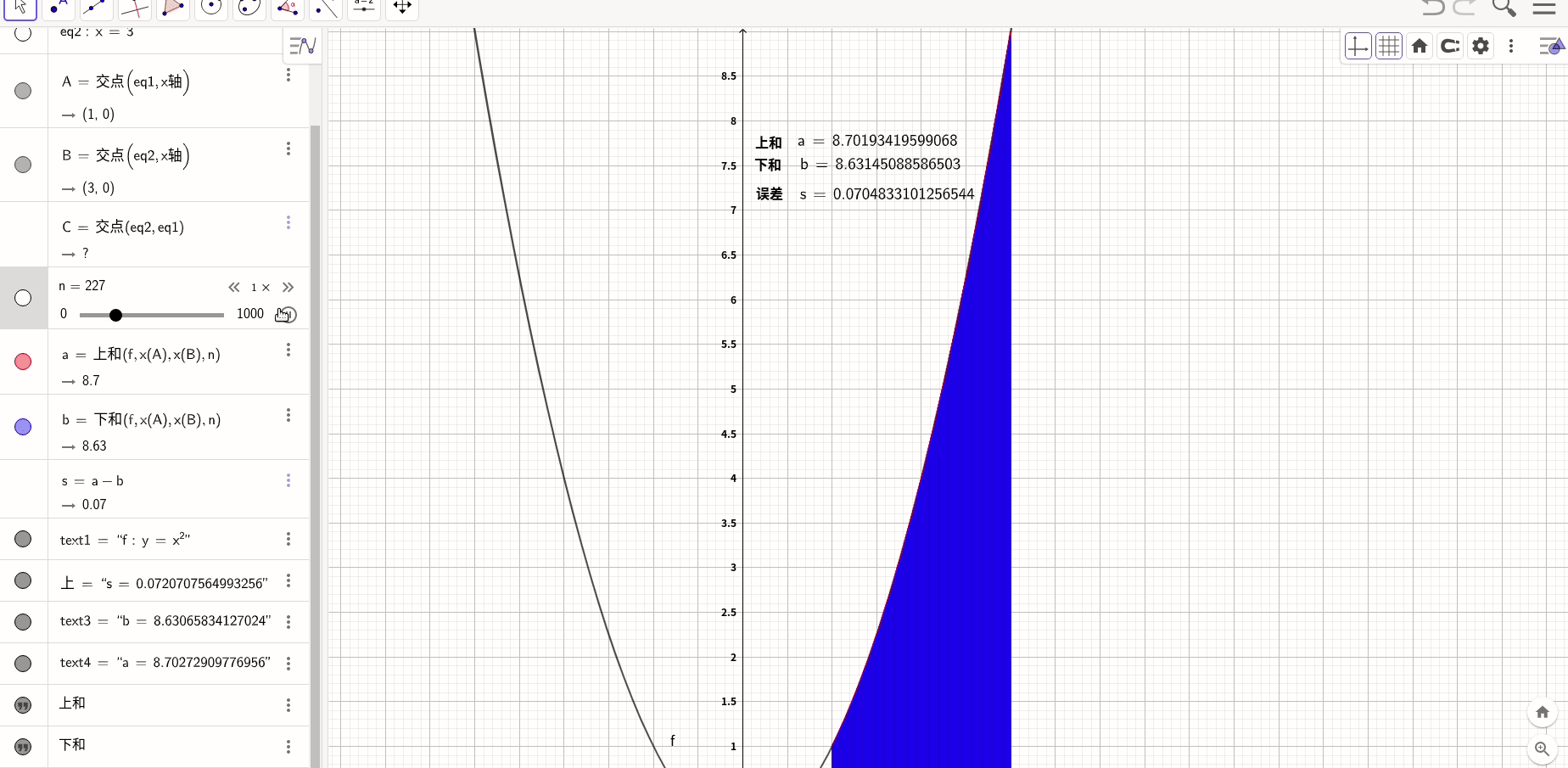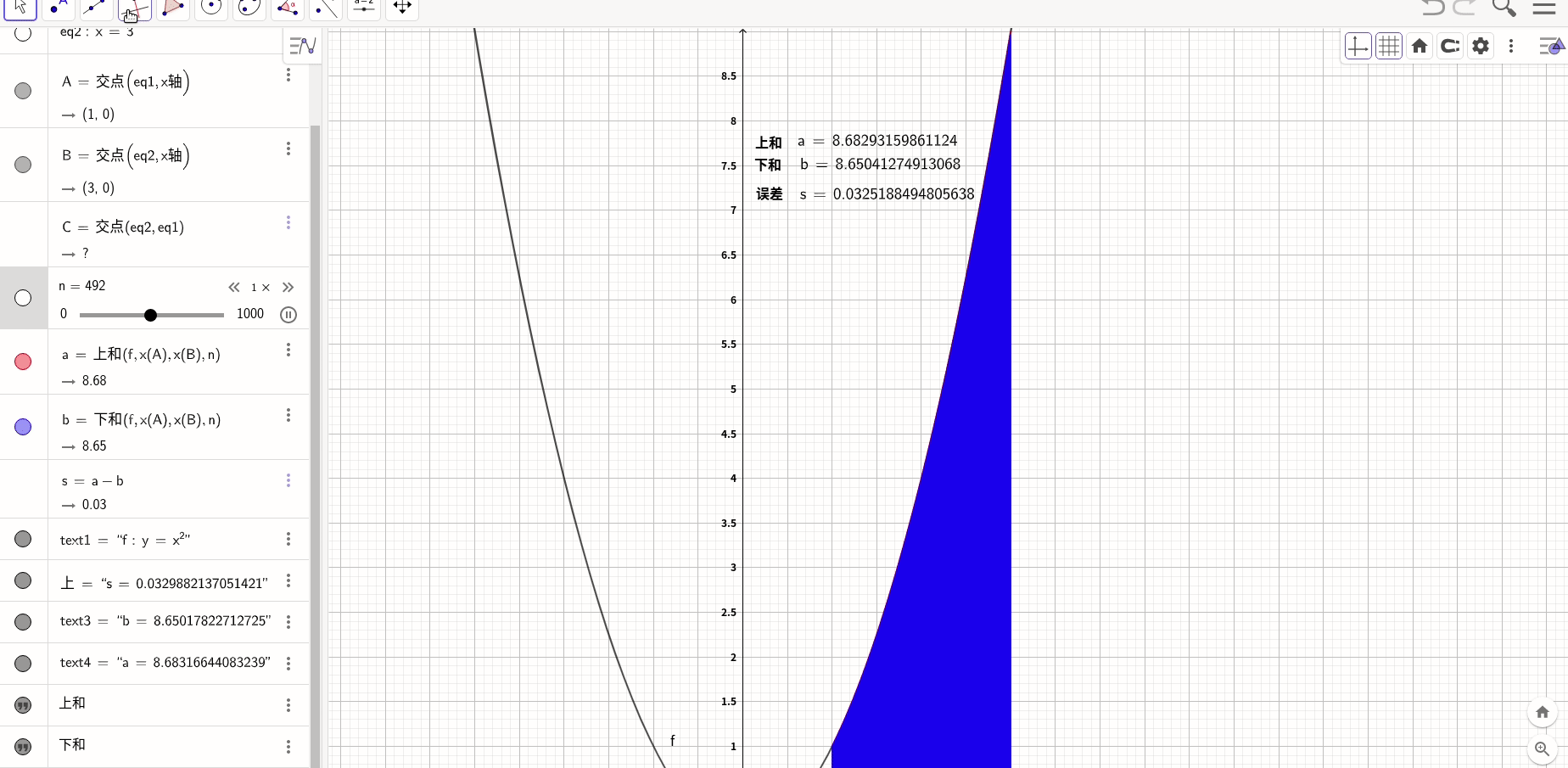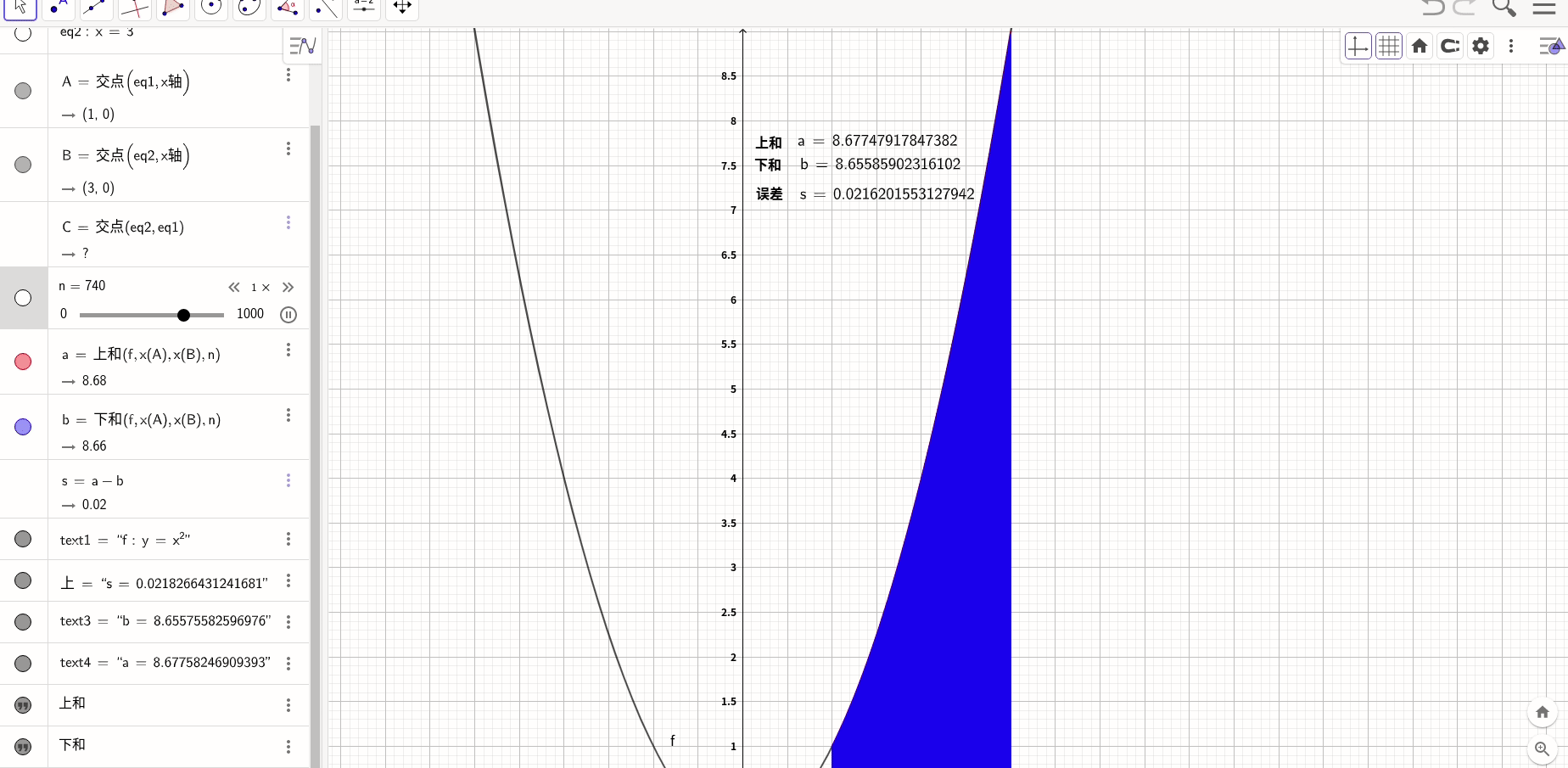
求PI
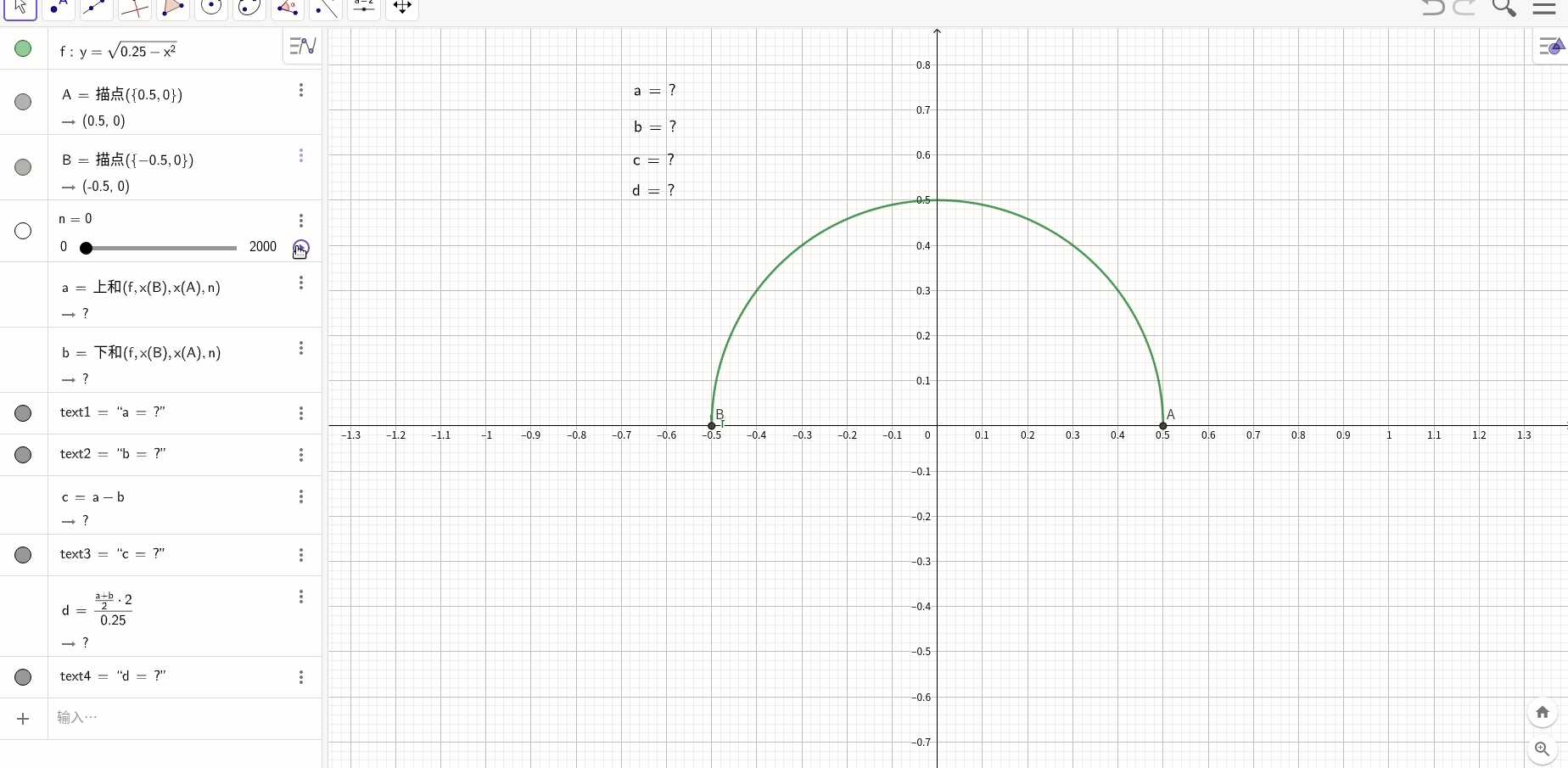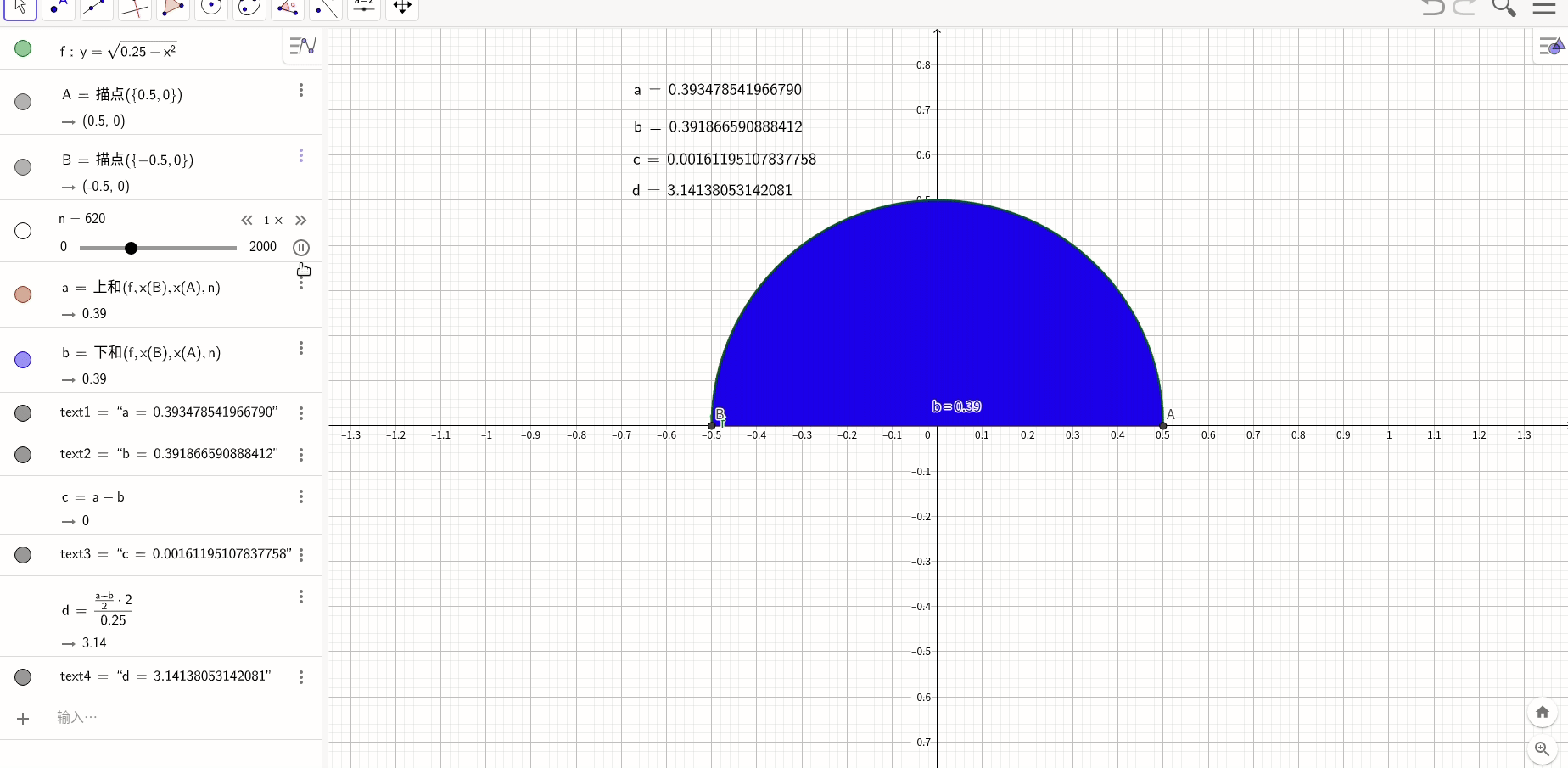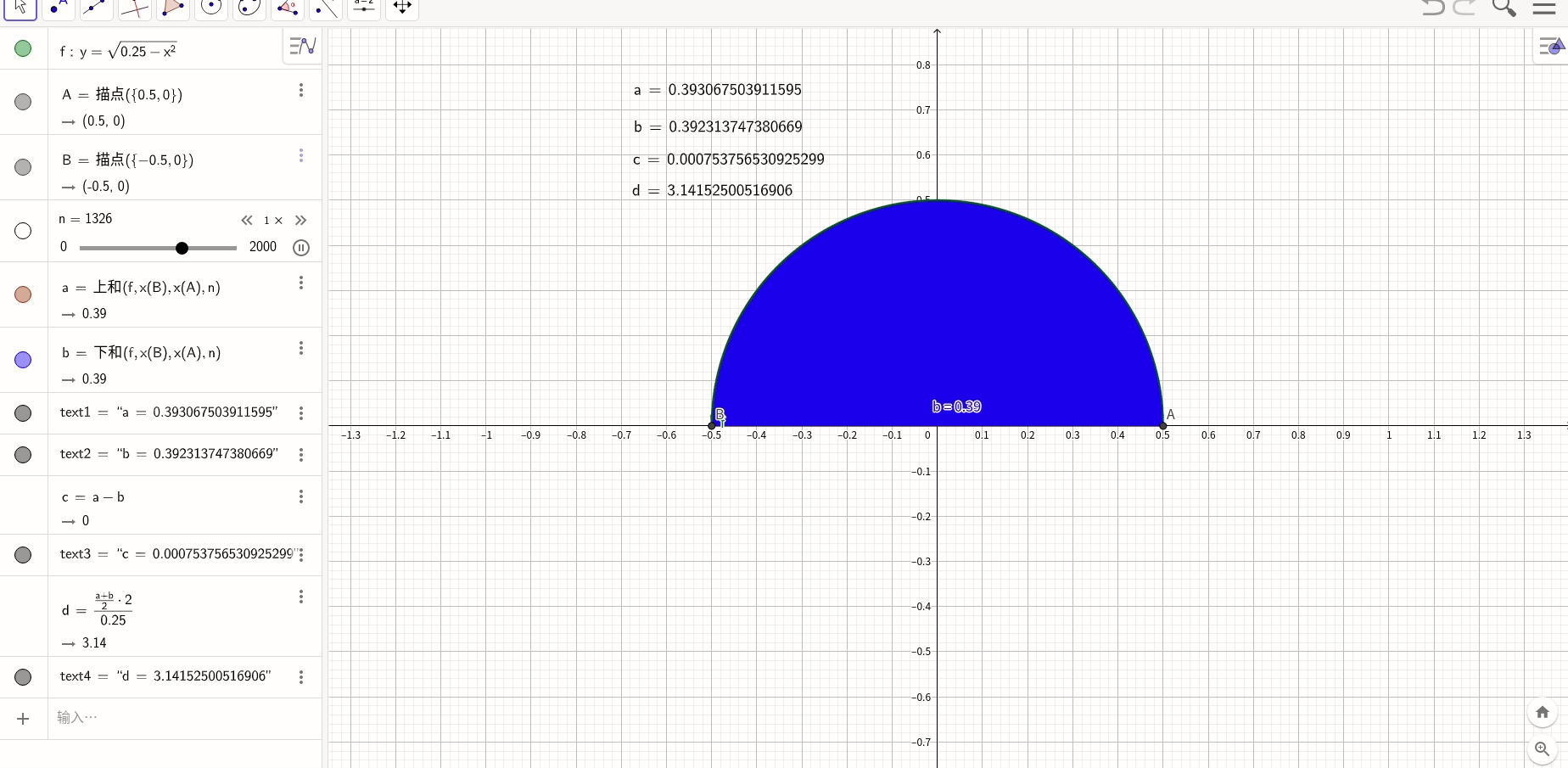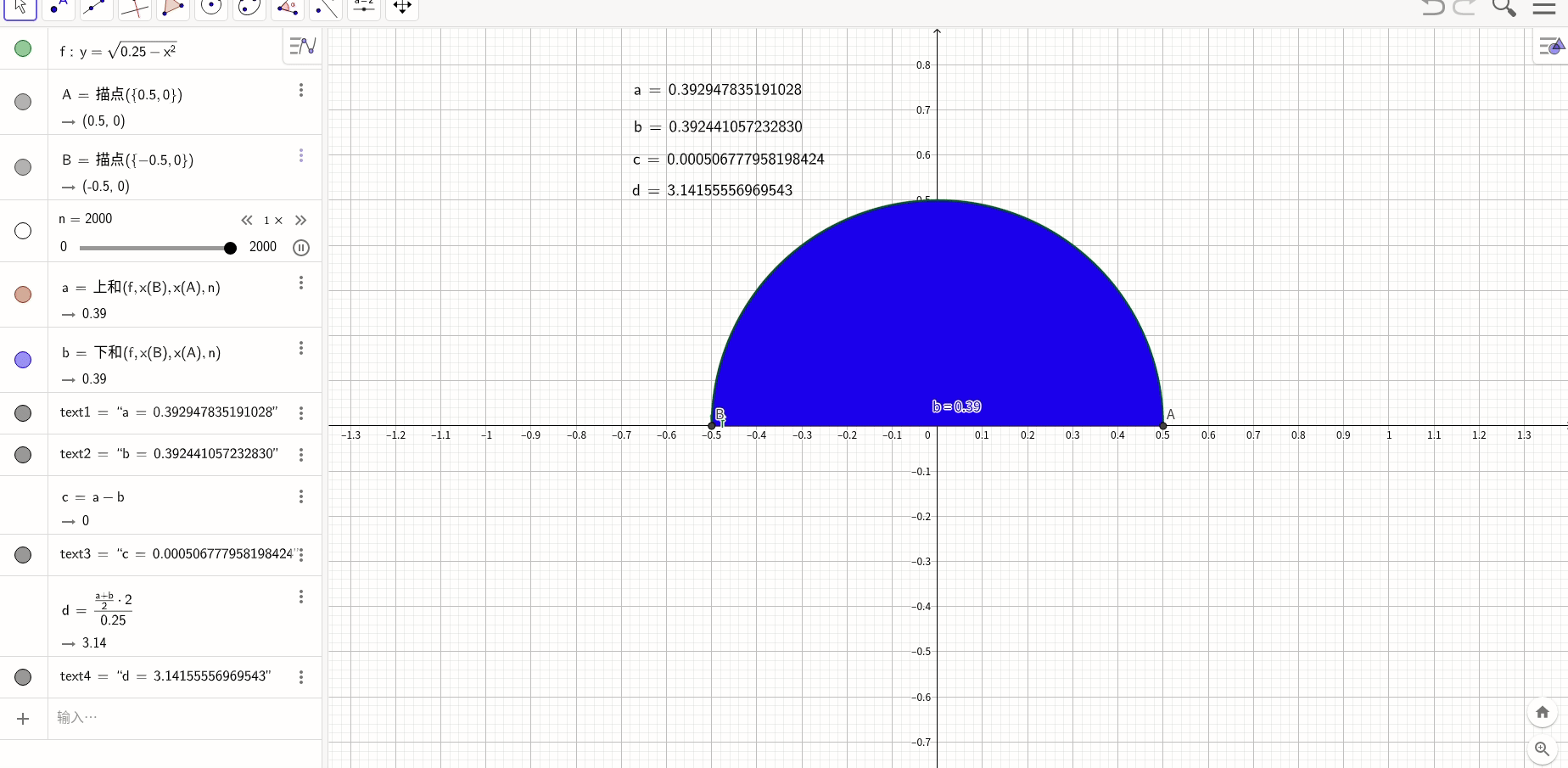
微积分的理解
有一些人认为微积分是错的,理由是推导过程中把不规则的图形分成若干小块,每一块近似成长方形后,都会产生误差,那么累加在一起之后,这些误差也会累积,所以最终肯定不等于原面积。
微积分理论是一套逻辑严谨,高度专业化的学术理论,遵循着专业的研究范式,微积分理论是建立在极限的集论之上的,在现代数学中,使用语言体系,对极限进行了严谨的定义,然后以此为基础,发展出了整套的微积分体系,这一过程复杂且严格。
在国外的专业教材上,采用的是和国内等价,但是略有不同表述的方式定义定积分的。就是,对于任意划分,以子区间的上确界作黎曼和做为达布上和,以下确界作黎曼和作为达布下和,如果所有达布上和的下确界等于所有达布下和的上确界,那么就称此界限为该函数的定积分。
微积分的定义是很严谨的,在现行体系下,我们可以证明定积分结果和实际是严格相等的。
求导数和求积分像是一把尺子,在丈量着这个世界无处不在的变化。
为什么积分比导数看起来难?
逆运算往往会突破原来的界限,导致跨域,加法的逆运算出现了负数,乘法的逆运算出现了小数,开方出现了无理数,数学上把这种突破界限叫做打破了封闭性。积分是求导的逆运算,也打破了封闭性。一个初等函数求导数还是一个初等函数,但是给一个初等函数求积分,可能是一个超越函数或者不知道是什么的函数,从一个哲学的角度来思考这个问题,求导数是已知全貌,要去判断局部变化性质。而求积分是知道局部,要去窥探全貌,后者就像盲人摸象一样,难以看清全局。这就是积分比导数难的原因。
曲线长度曲线积分
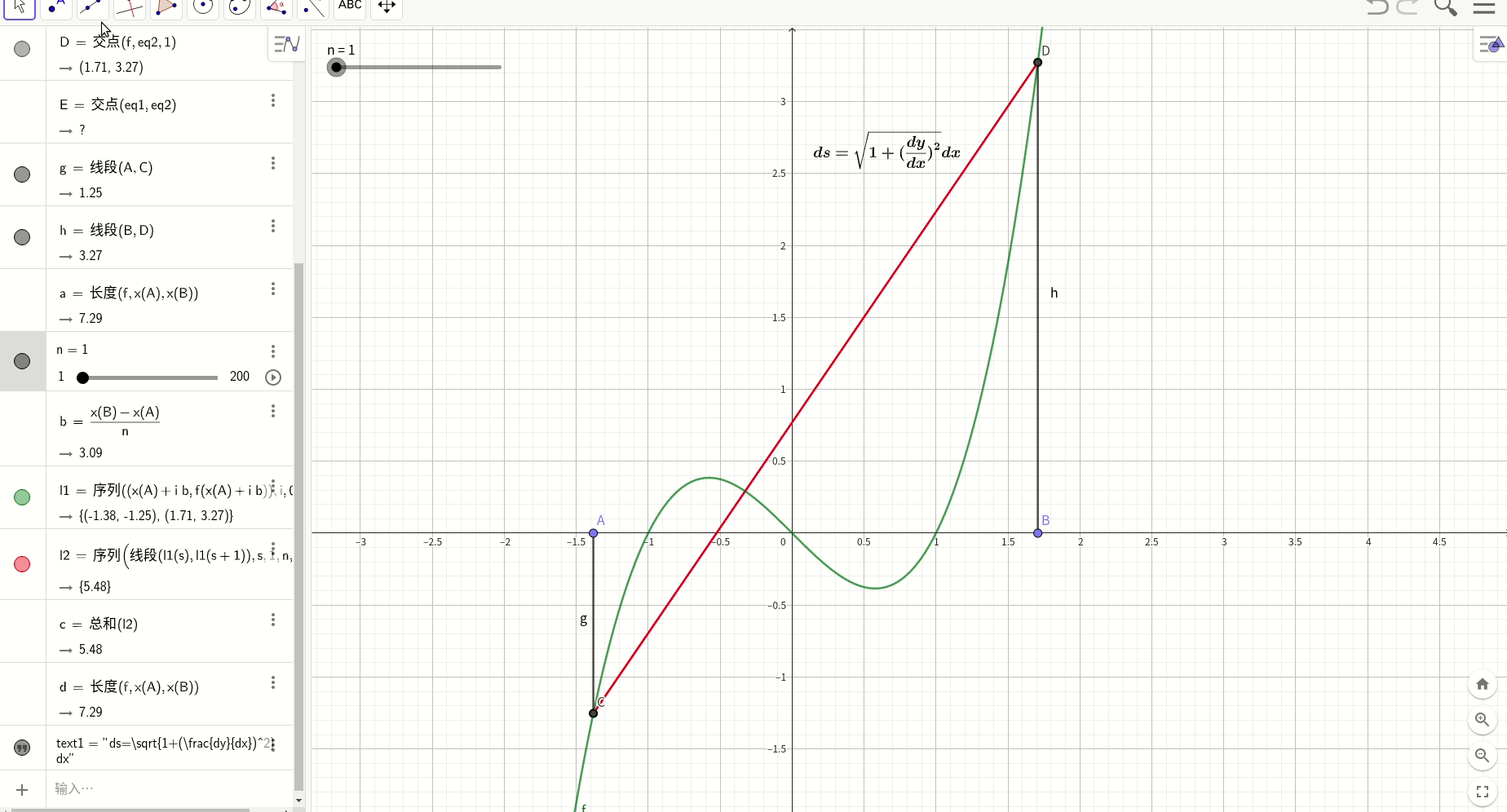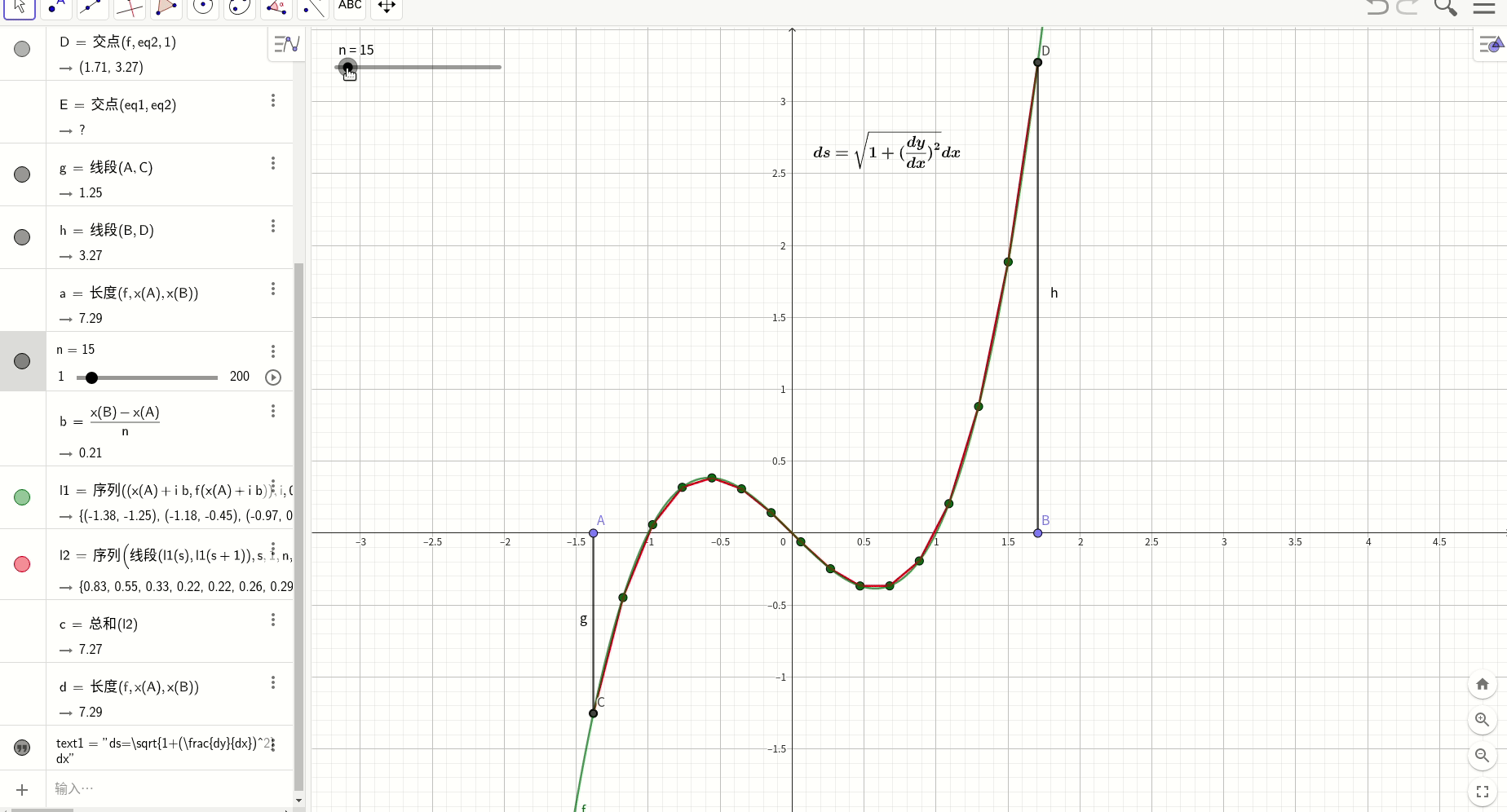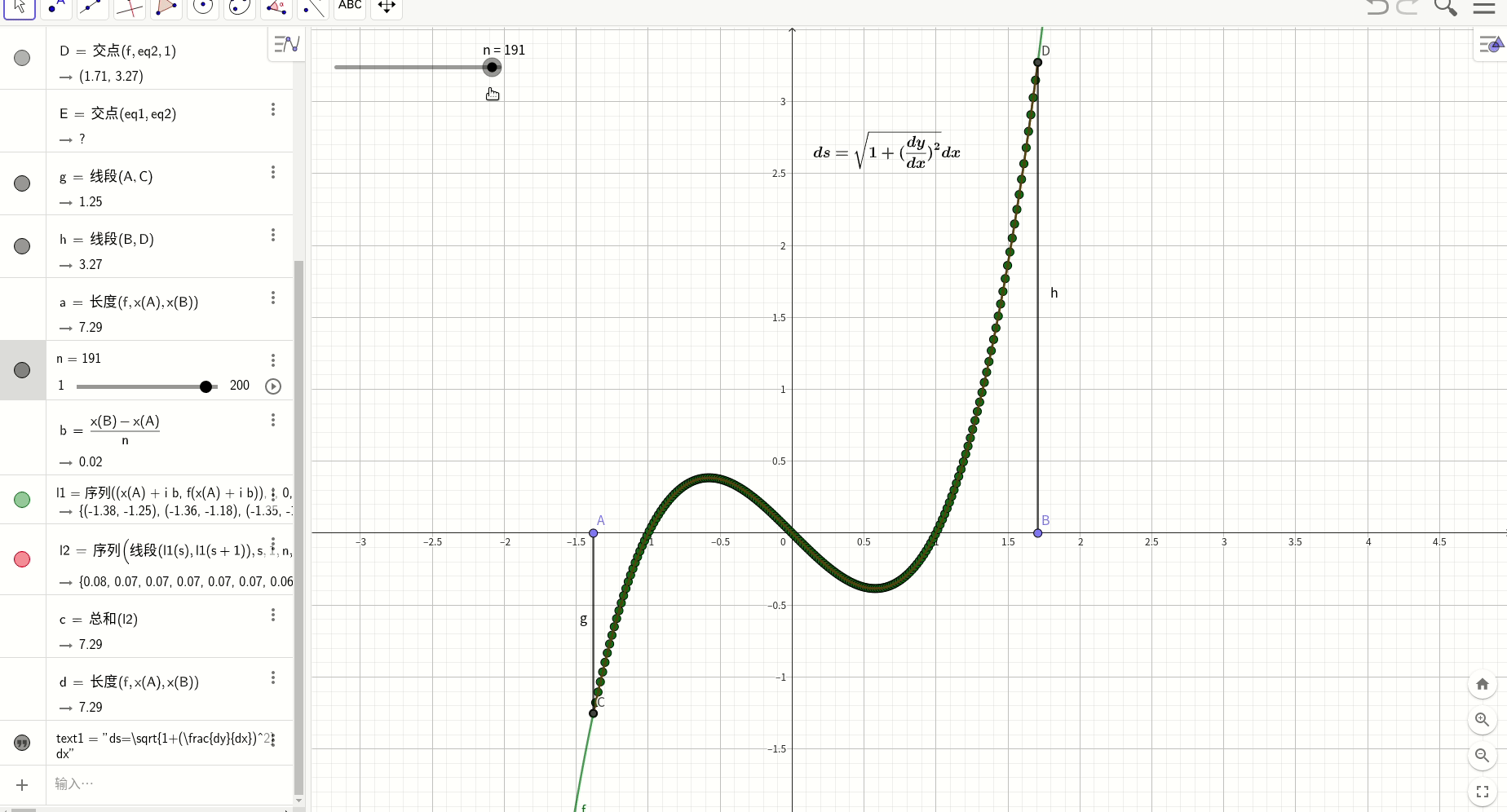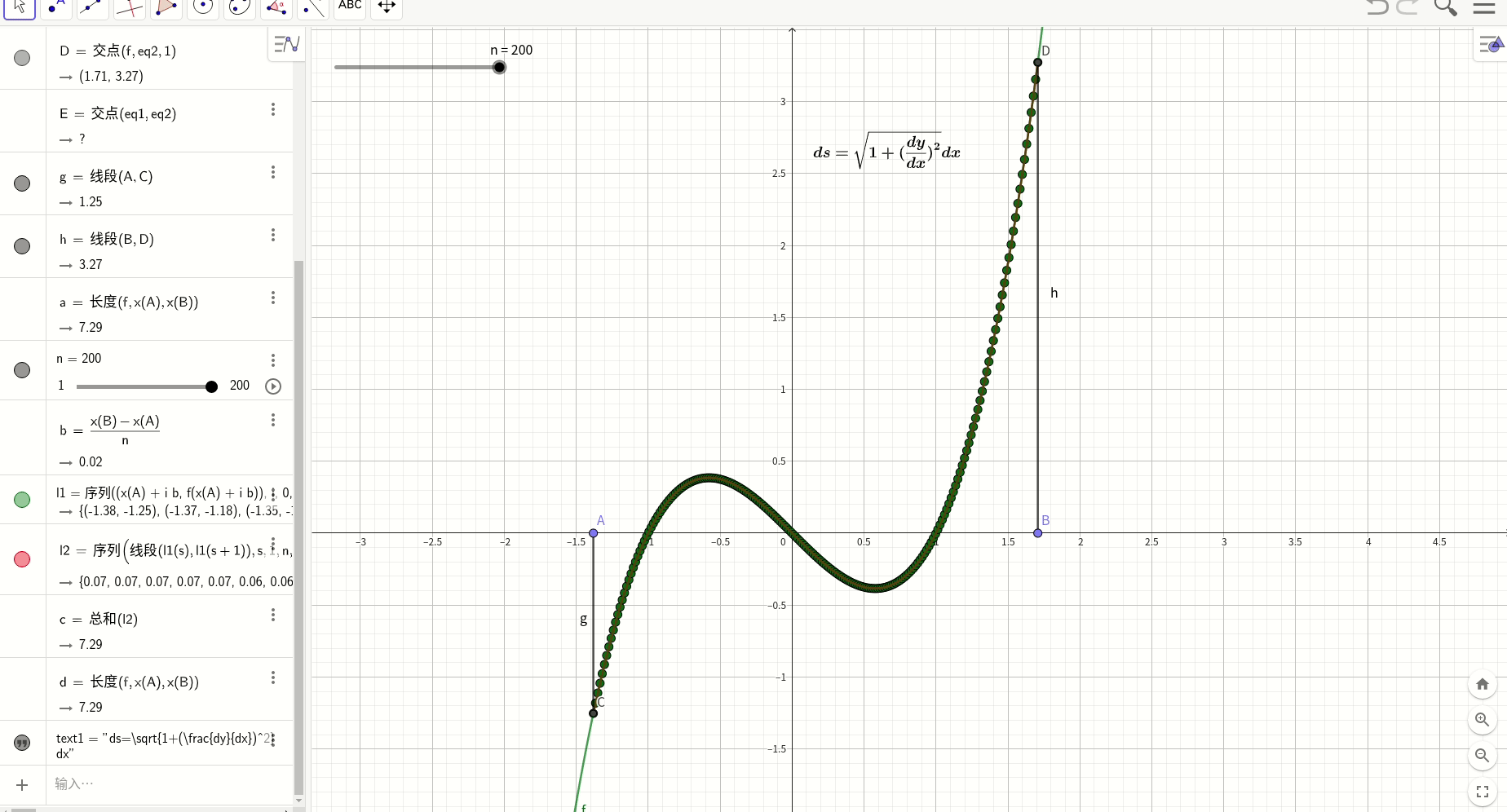
定积分图形化工具desmos
计算定积分的图形化工具desmos:Desmos | 图形计算器

差分机原理
差分机是英国数学家把巴贝奇的天才发明,利用它,可以用机械方法计算多项式。其原理是通过一组多项式系数对函数进行插值制表的方法,这种差分机的具体计算方案也很好理解,一次函数的结果是个等差数列,这个差值就是一阶差;二次函数的结果数列,其一阶差的值是个等差数列,而这个等差数列的差值就是二阶差。也就是说,几次函数就有几阶差,而计算函数的值就只需要将阶差加上去往回推就可以了,整个过程大中只需要用到加减法。
三次函数有三阶差,其三阶差是6,而x^3的三阶导数也是6,似乎有某种相通之处。
差分机的原理如下图所示:

二阶

二阶多项式:






























 1428
1428

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










