升维与降维硬核分析干货【全面无坑版】

在现代计算机视觉领域，数据通常具有高维度特性，例如高清图像、视频帧以及复杂的特征表示。高维数据虽然能够提供丰富的信息，但同时也带来了计算复杂度高、存储需求大以及模型训练困难等问题。为了解决这些挑战，升维（Dimensionality Expansion）和降维（Dimensionality Reduction）成为了两种关键的技术手段。本文将深入探讨升维与降维的数学基础、具体操作以及它们在计算机视觉任务中的实际应用与意义，通过具体例子帮助读者更好地理解这些概念的实质。

一、升维与降维的概述

1.1 升维

升维是指将数据从低维空间映射到高维空间的过程。其主要目的是通过引入新的特征，增强数据的表达能力，使得复杂的模式和关系在高维空间中更加显著，从而提升模型的性能。升维常用于处理非线性可分的数据，使其在高维空间中变得线性可分

1.2 降维

降维则是将高维数据映射到低维空间的过程，旨在减少数据的维度，同时尽可能保留原始数据中的关键信息。降维不仅能够降低计算复杂度，还能消除数据中的冗余和噪声，提高模型的泛化能力。常见的降维技术包括主成分分析（PCA）、奇异值分解（SVD）、t-SNE和UMAP等

二、升维与降维的数学理论基础

2.1 升维的数学基础

特征映射（Feature Mapping）

特征映射是一种将原始数据通过特定函数转换到高维空间的方法。假设有一个二维数据点 (x1,x2),通过特征映射函数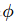可以将其映射到一个更高维的空间，例如

这种映射引入了新的特征，如平方项和交叉项，使得在高维空间中能够捕捉到数据的非线性关系

核技巧（Kernel Trick）

核技巧是一种在不显式计算高维特征空间映射的情况下，进行内积运算的方法。支持向量机（SVM）等算法常用核技巧，通过选择合适的核函数（如高斯核、多项式核等），隐式地在高维空间中进行升维操作，从而在高维空间中找到线性可分的超平面

希尔伯特空间（Hilbert Space）

升维通常涉及将数据映射到一个希尔伯特空间（无限维或高维的内积空间），利用高维空间的几何性质进行数据分析和处理。

实质

升维的本质在于通过映射函数为原始数据引入新特征，以便在更高维空间中更易寻找数据结构的内在规律或分类边界。升维经常与核方法（Kernel Methods）紧密相连：在核技巧（Kernel Trick）中，我们无需显式构造高维特征，只需定义满足Mercer条件的核函数便可在隐式高维空间中实现线性分割与拟合。这为传统的线性模型（如线性SVM）赋予了处理非线性问题的能力
深度学习中的升维也常体现在特征映射与通道扩展上。例如，卷积神经网络（CNN）在通过层叠的卷积和激活函数不断扩大特征维度（例如通道数），从而提取更具辨识度的中高层抽象特征。近期流行的Transformer架构中，Attention机制通过多头注意力（Multi-head Attention）对输入特征进行升维与重组，使得模型在更高维度的表示空间中捕捉数据的多重关系，从而提高特征表征的丰富度

2.2 降维的数学基础

主成分分析（PCA）

PCA是一种线性降维技术，通过线性变换将数据投影到新的坐标系中，使得投影后的数据在新坐标系上的方差最大。PCA的核心在于计算数据的协方差矩阵，并通过特征值分解找到主成分，这些主成分捕捉了数据中最大方差的方向

奇异值分解（SVD）

SVD将一个矩阵分解为三个矩阵的乘积，常用于数据压缩和降维。通过保留奇异值较大的部分，可以有效地减少数据的维度，同时保留主要信息

流形学习（Manifold Learning）

流形学习假设高维数据分布在一个低维流形上，常见的方法有t-SNE和UMAP。它们通过保持数据点之间的局部结构，实现非线性降维

信息理论（Information Theory）

降维过程中常涉及保留数据中的关键信息，如最大化信息保留量或最小化信息损失

实质

降维的实质是通过数学方法寻找数据中方差或信息量最集中的方向，并在保留主要信息的前提下压缩数据维度。线性降维方法中，主成分分析（PCA）借助协方差矩阵的特征值分解（Eigendecomposition）或奇异值分解（SVD）来选取主成分，从而在较低维的空间中保留数据最大的信息量。非线性降维方法（如t-SNE、UMAP、Isomap、LLE）则将降维问题视为流形学习（Manifold Learning）问题，假设高维数据分布在低维流形上，通过保持局部邻域结构进行降维，展现数据的内在低维结构。
在深度学习中，降维常与特征提取（Feature Extraction）、表示学习（Representation Learning）和自监督学习方法结合，用于减少模型输入的冗余性，缓解“维度灾难”（Curse of Dimensionality）。在大规模模型（如Vision Transformer、CLIP）中，对中间特征进行降维不仅有利于模型的推理与存储效率，也有助于提高模型的泛化性能和解释性。

三、升维与降维的具体操作与实例

3.1 升维的具体操作与实例

EXP1：支持向量机中的核技巧

假设我们有一个二维数据集，其中两类数据点在原始空间中呈现环形结构，难以用线性分类器分开。通过使用多项式核函数，将数据映射到高维空间：

在高维空间中，数据点可能变得线性可分，允许支持向量机找到一个线性超平面将两类数据分开。

EXP2: 矩阵升维示例

假设有一个 2×2 的数据矩阵：

通过升维操作，添加平方项和交叉项，得到一个 2×5 的矩阵

新增的特征帮助捕捉数据中的非线性关系，增强模型的表达能力

EXP3: 从非线性到线性可分

假设我们有一组二维数据分布在圆环上（即类别分布呈同心圆结构）。在线性模型的二维空间中，这两类数据不可线性区分,但如果通过映射将数据升维到三维空间，则同心圆数据变为不同高度的曲面分布，使得线性分割成为可能
在计算机视觉任务中，例如传统特征工程时代的HOG特征、SIFT特征等，通过构造空间梯度、方向梯度直方图等特征映射，实现了等效的升维过程：从原图像像素的原始空间迁移到具有判别力的特征空间

3.2 降维的具体操作与实例

EXP1：主成分分析在图像处理中的应用

考虑一个包含1000个特征的图像数据集，通过PCA将其降维到50维。PCA通过选择方差最大的前50个主成分，保留了大部分的信息，同时显著减少了计算和存储的需求。这在图像分类任务中尤为重要，因为降维后的特征更具代表性，能够提升分类器的效率和准确性

EXP2: 矩阵降维示例

假设有一个 3×3 的数据矩阵：

通过PCA将其降至3x2:

• 中心化数据：减去每列的均值。

• 计算协方差矩阵：
  

• 特征值分解：发现数据主要沿一个方向有方差

• 选择主成分：选择前两个主成分，得到降维后的矩阵：
  
  虽然降维后的矩阵维度减少，但通过保留主要的主成分，尽可能保留了数据中的重要信息

EXP3: 特征压缩与信息保留

给定一个1000维的图像特征描述子，使用PCA选取前100个主成分进行降维。这些主成分最大化了数据的方差，从而在很大程度上保留了数据的主要信息并去除冗余特征。这在图像检索、目标检测以及视频分析中尤为重要。例如，在使用大规模图像数据库进行相似度匹配时，降维后的特征向量能够显著加快相似检索的速度并减少存储成本。
在深度学习时代，降维还与知识蒸馏（Knowledge Distillation）或模型压缩（Model Compression）技术相结合，将大型模型的内部高维特征表示投影到较低维空间，从而在保持精度的前提下降低计算量和能耗。

四、应用场景

4.1 升维的应用场景

升维（增维）指的是通过某种方式将数据从一个较低的维度映射到较高的维度。升维的目的通常是为了引入更多的信息、帮助发现数据中的复杂模式或使某些算法（如线性分类器）变得有效

何时进行升维？

1、非线性可分问题：有时候，数据在原始空间中是线性不可分的，但通过映射到更高维度的空间后，数据可能变得线性可分。升维帮助将数据从低维空间“拓展”到高维空间，使得复杂的非线性问题变得线性可分

• 例子：支持向量机（SVM）中的核技巧（Kernel trick）就是典型的升维操作。通过将数据映射到一个高维空间，SVM能够找到一个更优的决策超平面，解决非线性可分的问题

2、引入更多信息：在一些情况下，升维是为了引入更多的特征，尤其是在数据的维度较低时，原始数据可能无法包含足够的语义信息或复杂的模式。升维可以通过增加新的特征、引入交叉特征等方式，扩展数据的表达能力

• 例子：在图像处理中，将原始的灰度图像通过增加颜色通道转为彩色图像，从而引入更多的颜色信息，有助于更好地进行图像识别

3、增加多模态数据的融合：多传感器数据（如RGB图像与深度图像、雷达数据与视觉数据等）通常会涉及到升维。不同的数据类型可能有不同的维度，融合这些数据时会涉及升维，确保不同模态数据的统一表示。

• 例子：在自动驾驶系统中，通常需要将激光雷达（LiDAR）的点云数据与相机图像数据进行融合。在这个过程中，相机图像的2D数据可能会通过某些方式（例如通过相机内参与外参）映射到3D空间，与激光雷达的3D点云数据融合

4、特征映射和生成特征空间：在机器学习中，尤其是对于那些没有明确特征空间定义的数据，升维有助于构建适合的特征空间。例如，通过使用多项式特征映射或者高斯核，原始的低维数据通过升维转化为一个高维空间，使得模型能在新的空间中有效工作

• 例子：多项式回归中，特征从原始的线性空间升维到高次多项式空间，允许模型学习到非线性关系

何时避免升维？

升维虽然能够增加数据表达能力，但也会带来一些潜在的问题：

• 维度灾难：在高维空间中，数据变得稀疏，计算复杂度急剧上升，模型容易陷入“过拟合”。
• 数据过于复杂：升维后可能引入过多的冗余信息，导致数据的复杂度增加而无法有效训练模型。

因此，在数据已经足够表达问题时，或者已经有足够的特征信息时，升维往往是不可取的。

4.2 降维的应用场景

降维是指通过某些方法将数据从一个高维空间映射到一个低维空间。降维的目的是简化数据的结构，去除冗余信息，减少计算复杂度，或者发现数据的潜在结构。

何时使用降维？

1、减少噪声和冗余特征：高维数据往往包含大量冗余的或无关的特征，这些特征可能会干扰模型的训练，导致过拟合。降维能够去除不必要的特征，简化模型

• 例子：在基于PCA（主成分分析）进行降维时，通过选择数据中最具方差的主成分，可以去除噪声，保留最有用的信息

2、降低计算复杂度：当数据维度过高时，处理和存储这些数据的计算代价会急剧增加。降维可以显著减少数据的存储和计算成本，尤其在数据量大、计算资源有限时尤为重要

• 例子：在自然语言处理中，文本数据通常是非常高维的，通过TF-IDF或者Word2Vec等方法进行降维（例如将词向量降到200维或更低），可以大大提高计算效率

3、可视化：当数据的维度较高时，人类难以直观地理解数据的结构和分布。通过降维，可以将数据映射到2D或3D空间进行可视化，帮助理解数据的内在结构

• 例子：在高维数据集（如文本数据或基因数据）中，使用t-SNE或PCA将数据降到二维或三维，可以帮助我们发现不同类别数据之间的关系和分布

4、提高模型泛化能力：降维有助于去除数据中的噪声，减少过拟合的风险。通过将数据压缩到一个更简洁的空间，模型能够专注于重要的模式和特征

• 例子：在深度学习中，通过卷积操作进行降维（如卷积层的步长和池化操作），可以减少特征的空间维度，提升模型的计算效率，防止过拟合

5、特征选择与重要性评估：有时我们进行降维是为了选择最重要的特征，去除不相关的特征，这对于提高算法效率和可解释性非常有帮助

• 例子：使用LDA（线性判别分析）等方法进行降维，选择能最好区分不同类别的特征，进行后续的分类或聚类。

何时避免降维？

• 信息丢失：降维可能会丢失一些关键信息，尤其是当数据的维度降低得过多时，可能会丧失对问题的准确描述。因此，降维的过程中必须平衡信息保留和数据简化之间的关系。
• 复杂度增加：某些降维技术，如t-SNE等，可能会增加计算复杂度，尤其是在数据量巨大时，可能不适合使用。

升维与降维的权衡

升维和降维之间的选择需要基于任务需求和数据特点：

• 升维：适合用于提升模型的表达能力，解决非线性可分问题，引入更多的特征信息。在数据维度较低且问题复杂时升维可以显著提升模型的性能，但也可能引发“维度灾难”
• 升维主要用于解决非线性可分问题、引入更多信息或在多模态数据融合时提供统一的表示。其典型应用包括SVM核技巧和多传感器数据融合
• 降维：适合用于去除冗余特征、简化计算、提高模型效率。在高维数据中，降维能够帮助消除噪声、减少计算复杂度，防止过拟合
• 降维则常用于去除冗余特征、简化计算、提高效率或进行数据可视化。其典型应用包括PCA、t-SNE等方法

五、应用与意义

5.1 升维

特征工程和深度学习

在深度学习中，特别是卷积神经网络（CNN）中，升维通过堆叠多个卷积层和增加特征图的通道数，使得模型能够学习到更高阶的特征。例如，初级卷积层可能学习到边缘和纹理，而更深层的卷积层则能够捕捉到更复杂的形状和对象部分。这种逐层升维的过程增强了模型的表达能力，提高了其在复杂视觉任务中的性能。

核方法与非线性分类

使用核方法（如RBF核）将数据映射到高维空间，使得在高维空间中数据变得线性可分，从而提升分类器的性能。例如，在人脸识别中，通过升维可以更好地区分不同人的面部特征，增强识别的准确性。

5.2 降维

图像压缩与存储

降维技术，如PCA和SVD，广泛应用于图像压缩。通过减少图像的维度，可以显著降低存储需求，同时保留图像的主要视觉信息。例如，使用SVD对图像进行分解，仅保留最大的奇异值和对应的奇异向量，可以实现高效的图像压缩。

特征提取与去噪

在特征提取过程中，降维有助于去除数据中的噪声和冗余信息，提升特征的质量。例如，在手写数字识别中，降维可以减少特征空间的复杂性，提升分类器的泛化能力。同时，降维还能提高计算效率，加快模型训练和推理的速度。

数据可视化

高维数据的可视化是理解和分析数据的重要手段。通过降维技术，如t-SNE和UMAP，可以将高维数据映射到二维或三维空间，便于人类直观地观察数据的分布和结构。例如，在图像分类任务中，降维后的特征可以用来可视化不同类别的数据分布，帮助识别数据中的潜在模式和关系

5.3 意义

与深度神经网络的融合

在深度学习中，升维和降维并不仅仅是数据预处理的手段，而是嵌入在模型架构本身的策略。以Transformer为例，多头注意力机制通过线性映射将输入特征升维到更高维的查询（Q）、键（K）、值（V）空间，使模型能够在高维空间中灵活地匹配上下文关联。在输出层，降维操作则可将高维嵌入投影回较低维输出空间，提高模型的推理速度

大模型与多模态数据

随着AI模型规模的指数级增长（如GPT、CLIP、PaLM、Vision-Language Models）和多模态数据的广泛应用（图像、文本、点云、音频和视频同时处理），高维特征空间的结构愈发复杂。升维与降维在此类大模型中有如下意义：

• 升维：通过扩张特征空间的维度，大模型可以更高效地融合不同模态信息。例如，在多模态Transformer中，通过升维的投影层将图像特征与文本特征映射到共享的高维表示空间，以便进行统一建模。

• 降维：在多模态场景中，数据往往异常高维且存在冗余。降维技术可帮助简化特征表示，使模型以更低的计算成本获得良好的性能，并有助于在后处理阶段进行可视化、解释和调试。

信息瓶颈与表示学习

在表示学习领域，“信息瓶颈”（Information Bottleneck）理论为降维提供了新的视角。模型在训练过程中通过内部表示的降维与信息压缩，过滤掉与任务无关的噪声特征，凸显核心判别信息。升维与降维在此层面体现为对信息流动路径的精巧设计：网络通过升维增强特征表达能力，通过降维凝练信息，从而达到更高的性能与鲁棒性。

六、总结

升维与降维是计算机视觉中处理高维数据的两种基本而重要的技术手段。升维通过引入新的特征，增强了模型的表达能力，使其能够捕捉到更复杂的模式和关系；而降维则通过减少数据的维度，去除冗余和噪声，提高了数据处理的效率和模型的泛化能力。两者在计算机视觉的多个任务中发挥着关键作用，如图像分类、目标检测、图像压缩和特征提取等。理解升维与降维的数学基础和实际操作，不仅有助于更好地应用这些技术，还能为设计更高效、更精准的计算机视觉模型提供理论支持。随着计算机视觉技术的不断发展，升维与降维将在数据处理和模型优化中继续扮演重要角色