Collective Matrix Factorization Hashing for Multimodal Data--文献翻译

MT_Joy

已于 2022-03-15 10:12:29 修改

阅读量1.3k

点赞数 2

分类专栏：有监督的跨模态哈希 # 1、基于标签矩阵语义的跨模态哈希 # 2、基于矩阵分解的方法文章标签：算法哈希算法矩阵人工智能

于 2022-03-08 15:19:24 首次发布

本文链接：https://blog.csdn.net/qq_42014059/article/details/123312452

版权

有监督的跨模态哈希同时被 3 个专栏收录

6 篇文章

订阅专栏

1、基于标签矩阵语义的跨模态哈希

5 篇文章

订阅专栏

2、基于矩阵分解的方法

5 篇文章

订阅专栏

本文提出了一种名为集体矩阵分解散列（CMFH）的新方法，用于在多模态数据的跨视图相似性搜索中学习哈希函数。CMFH通过集体矩阵分解和潜在因子模型从不同视图学习统一的哈希码，不仅支持跨视图搜索，还能通过融合多视图信息提高搜索精度。实验结果显示，CMFH在多个数据集上优于现有先进方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

摘要：

基于散列的最近邻搜索方法在计算机视觉和信息检索社区中有效和高效的大规模相似性搜索引起了相当大的关注。在本文中，我们研究了在跨视图相似性搜索的多模态数据上下文中学习哈希函数的问题。我们提出了一种新颖的散列方法，称为集体矩阵分解散列（CMFH）。 CMFH通过集体矩阵分解和潜在因子模型从一个实例的不同模态中学习统一的哈希码，不仅可以支持跨视图搜索，还可以通过合并多个视图信息源来提高搜索精度。我们还证明了CMFH，一种保持相似性的散列学习方法，具有上限和下限。大量实验证实，CMFH 在三个不同的数据集上显着优于几种最先进的方法。

1、介绍

最近邻搜索在许多重要应用中发挥着重要作用，例如信息检索、数据挖掘和计算机视觉。基于散列的最近邻搜索是最知名的将高维数据嵌入到紧凑二进制码字中的方法，近年来因其在海量数据中的巨大效率提升而引起了相当大的兴趣[8]。最著名的基于散列的模型之一是局部敏感散列（LSH）[6]，其基本思想是将原始数据映射到汉明空间，同时以高概率保持它们的相似性。 LSH 可以非常有效地处理相似性搜索，因为在计算二进制码之间的汉明距离时应用了位 XOR 操作 [24]。作为标准 LSH 的扩展，一些机器学习方法被用于设计有效的紧凑散列，例如流形学习、监督学习、内核学习、深度学习、量化学习、线性判别分析 (LDA)、K-means 和 PCA，它们分别生成光谱散列 [22]、监督散列 [13]、核散列 [11]、语义散列 [17]、迭代量化散列 [7]、LDA 散列 [20]、Kmeans 散列 [9] 和 PCA 散列 [21]。

随着相似性搜索在不同视图中的扩展，上述的单视图方法被扩展到多视图场景。跨视图哈希函数学习的核心问题是如何处理从不同概率分布中采样的多模态数据。最近，已经开发了一些交叉视图哈希方法。通常，交叉视图哈希方法可以分为两类：视图特定的哈希方法和集成方法。特定于视图的哈希方法学习实例的每个视图的独立哈希代码，然后连接多个特定于视图的二进制代码，以获得集成的哈希代码。在[3]中，通过将不可通约的数据嵌入到一个公共度量空间来解决交叉模态相似度搜索哈希(CMSSH)的求解，并利用特征分解和标准的AdaBoost来学习哈希函数。在[12]中，Kumar等人将光谱哈希扩展到多视图场，并提出了一个交叉视图哈希模型(CVH)，该模型通过求解一个广义特征值问题，使对象对的加权平均多视图2-范数距离最小化。共正则化哈希(CRH)[26]的目标函数旨在投影远离0的数据以获得良好的泛化，同时有效地保持模态间的相似性。媒体间哈希(IMH)[19]引入了媒体间一致性和媒体内一致性来发现一个共同的汉明空间，并使用线性回归与正则化模型来学习特定于视图的哈希函数。上述的哈希方法主要用于不同视图之间的相似性搜索。例如，给定一个图像作为查询，搜索引擎可以返回一些文档来准确地描述细节。要实现交叉视图搜索，每个视图都需要存储独立的哈希代码，这就增加了存储和搜索的成本。

集成哈希方法为每个实例学习统一的散列码。具有多个信息源的复合散列（CHMIS）[23] 通过优化松弛散列码和组合系数，将来自不同来源的信息组合成最终的集成散列码。或者。多视图频谱散列（MVSH）[10]将多视图信息集成到二进制代码中，并使用代码字的乘积来避免不希望的嵌入。这种散列方法一般用于通过组合一个实例的多个信息源来提高散列码的搜索精度，而不是用于跨视图相似搜索。只有当所有信息源都可用时，它们才能正常工作，这在现实世界中要求太高。

在本文中，我们提出了一种新颖的散列方法，称为集体矩阵分解散列（CMFH）。 CMFH 假设一个实例的每个视图都生成相同的哈希码，而不是来自不同视图的一些哈希码的组合或串联。图 1 说明了上述两类方法与 CMFH 之间的区别。对于每个实例，我们通过使用来自不同视图信息源的潜在因子模型的集体矩阵分解来学习统一代码。为了确保学习的哈希码可以被搜索到不同的视图，我们还为每个视图学习线性哈希函数以确定未见过实例的二进制代码。我们的论文有以下贡献：

1、我们提出了一种跨视图场景下的统一哈希方法，不仅可以支持跨视图搜索，还可以通过合并多个视图信息来提高搜索精度。

2、我们的工作是首次尝试使用集体矩阵分解（CMF）技术来学习交叉视图散列函数。我们的实验表明，当有多个视图信息源可用时，CMF 是一种有效的散列方法。

3、我们表明，所提出的 CMFH 是一种具有近似 biLipschitz 连续性的相似性保留散列方法，如 3.6 所示。

我们对三个不同数据集的广泛实验研究突出了我们的方法在交叉视图场景下的优势，并验证 CMFH 显着优于几种最先进的方法。本文的其余部分安排如下。我们在第 2 节中简要介绍了集体矩阵分解和代表性交叉视图散列方法的相关工作。第 3 节介绍了我们提出的方法。第 4.1 节提供了对三个数据集的广泛实验验证。结论在第 5 节中给出。

图 1. 三种方法的区别。

2 相关工作

2.1协同矩阵分解

在关系学习方面，[18]提出了协同矩阵分解方法来预测给定一个实体数据集的未知关系值，并观察到两者之间的多个关系实体CMF联合分解了可能具有不同值类型的多个关系矩阵，当实体出现在多个关系中时，这些因子共享参数。以[18]中的电影评分预测为例。设 $X\in R^{m\times n}$ 为表示用户评级的整数矩阵，元素 $X_{ij}$ 表示用户i对电影j的评级。设Y∈ $R^{r\times n}$ 是一个二进制矩阵，表示每个电影所属的类型， $Y_{ij}$ 表示电影j是否属于类型i。因子是U∈ $Y^{m\times k}$ ，V∈ $R^{n\times k}$ 和Z∈ $R^{r\times k}$ ，V是重构中的共享因子：X≈ $f_{1}$ (U $V^{T}$ )和Y≈ $f_{2}$ (Z $V^{T}$ )，其中fi是一个可能的非线性链接函数，k>0是秩。平均可分解损失为：

其中，L1，L2分别为X≈ $f_{1}$ (U $V^{T}$ ))和Y≈ $f_{2}$ (Z $V^{T}$ )和 $a_{t}$ =1的可分解损失函数。

不局限于电影评级预测，CMF是一种简单而强大的方法来处理许多应用程序，其中有多个相互关联的数据源可用，它们不能用一个邻接矩阵[2]来表示。在多媒体领域中，对象通常以几个不同的视图呈现，例如，维基百科的相同主题的页面可能以图像、文本或两者的形式出现。据我们所知，我们是第一个应用CMF来学习在多模态数据上搜索的相似性的哈希函数。

2.2.视图特定的哈希方法

特定于视图的哈希方法为实例的每个视图学习独立的哈希代码，然后连接特定于视图的二进制代码，以获得集成的哈希代码。

CVH[12]为对象 $o_{i}$ 、∀t、i的视图t设计了一组二进制码{ $y_{i}^{(t)}$ }，并最小化加权累积汉明距离：

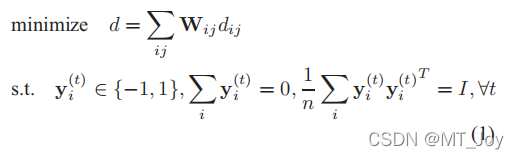
其中，≥t||(t)−yj(t)||2表示oi和oj之间的累积汉明距离，Wij表示oi和oj之间的相似性。最后，假设了一个低维的线性嵌入：yi(t)=a(t)tx(it)，它将方程（1）转化为一个广义特征值问题

CMSSH[3]以监督的方式将两个任意空间的输入数据嵌入到汉明空间。给定对(xk，yk)和相似性标签sk∈{+1，−1}，这里xk∈Rm，yk∈Rn从不同的空间采样。CMSSH定义了形式为fi(x)=pTix+ai和gi(y)=qTiy+bi的仿射投影，然后通过最大化生成第i位：

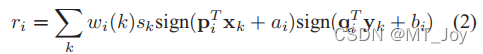
其中，wi(k)是Adaboost[1]中的加权系数，wi(k)为(xk，yk)增加，否则减少。放弃符号函数，方程（2）与一个更简单的函数密切相关：

其中，xk和yTk是xk和yk，以它们的加权均值为中心，以及vk=wi(k)sk。方程（3）可以通过奇异值分解求解，通过数据库框架可以生成多个哈希位。

2.3.集成的哈希方法

集成的哈希方法只为每个实例学习一组统一的哈希代码。CHMIS[23]使用一个码字yi∗来表示一个对象，并测量每个单独源上的汉明距离并将它们相加：tijW(t)ijyi∗−yj∗2，，其中W(t)是第t个源的亲和矩阵。为了方便地将解扩展到样本外数据点，CHMIS假设yi∗=符号(tαt(M(t))x(it))，其中M(t)是t-th源的权重矩阵，α={αt}是与tαt=1的非负凸组合。CHMIS最小化值：

MVSH[10]构造了一个平均相似度矩阵W，并将多个视图信息集成到统一的二进制码中，命名为yi∗=符号(tM(t)xi(t))，其中M(t)为投影矩阵。为了避免不良的嵌入，MVSH定义了dij=(yi∗)Tyj∗来测量oi和oj之间的汉明距离。因此，MVSH可以最小化了：

3.协同矩阵分解哈希

在本节中，我们将介绍我们针对多种模态数据的哈希方法，即集体矩阵分解哈希(CMFH)。在不失一般性的情况下，我们首先在双峰情况下引入CMFH，因为它简单易理解。

3.1.问题公式

假设O={oi}ni=1是一组多视图对象和 $X^{1}$ =[ $X_{1}^{(1)}$ ，...， $X_{n}^{(1)}$ ]， $X^{(2)}$ =[ $X_{1}^{(2)}$ ，...， $X_{n}^{(2)}$ ]是两个不同的视图矩阵，其中 $X_{i}^{(1)}$ ∈ $R^{d_{1}}$ ， $X_{i}^{(2)}$ ∈ $R^{d_{2}}$ (通常，d1=d2)。给定码字长度k，CMFH的目的是学习oi，i=，1,2，...，n的统一哈希码yi∈{−1,1}k，这样 $y_{i}$ ， $y_{j}$ 以高概率保持 $o_{i}$ 和 $o_{j}$ 之间的相似性。

3.2.框架概述

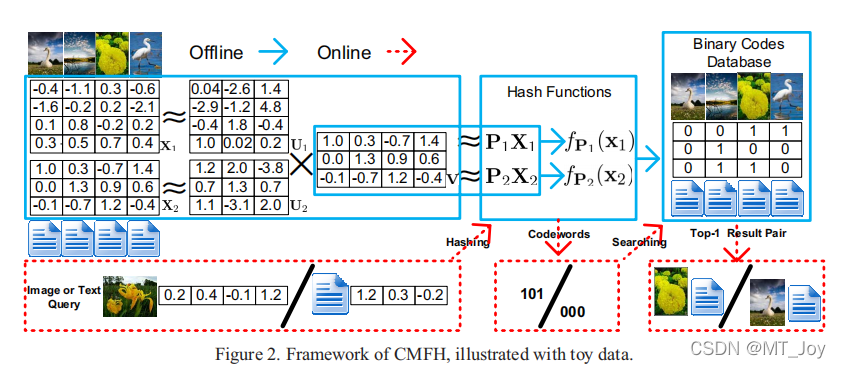
如图2所示，建议的CMFH包括两个阶段。一个是离线哈希函数学习和数据库生成，另一个是在线编码和搜索。在离线阶段，CMFH学习统一的哈希码Y=[y1，...，yn]。对于样本外实例，CMFH学习视图特定于t的哈希函数。与之前的工作[21,12,3]类似，我们只考虑该形式的仿射投影。

其中 $P_{t}$ ∈Rk×dt是投影矩阵，在 $a_{t}$ ∈Rk是偏移单位向量。在在线阶段，任何类型的查询都将根据相关学习到的哈希函数映射到紧凑的代码，即给定查询x(t0)，通过y=符号(ft0(x(t0))生成统一的哈希字。然后，CMFH返回给定映射查询的所有视图的类似结果。CMFH对于在线相似度搜索任务是非常有效的，因为在计算二进制码之间的汉明距离时采用了位XOR操作。

3.3.集体矩阵分解哈希

我们可以通过矩阵分解[5]从源数据集中学习潜在的语义特征：

1、其中 $U_{t}$ $\in$ $R^{d_{t}\times k}$ ， $V_{t}$ $\in$ $R^{k\times n}$ 和k为潜在因素的数量。每个列向量vt都是第t个视图数据x(t)的潜在语义表示。我们假设,相互关联的数据应该具有相同的潜在语义表示；

2、哈希码可以从潜在的语义表示中学习，即y=符号(v)。

其中Ut∈Rdt×，Vt∈Rk×n和×为潜在因素的数量。每个列向量vt都是第t个视图数据x(t)的潜在语义表示。我们假设

基于假设1，我们联合分解X（1）和约束V1=（2）：

这里的λ是平衡参数。数据库的Y可以根据假设2直接得到，但不能推广到直接查询。对于样本外实例，CMFH学习公式（4）中形式的第t个视图ft的哈希函数特定视图。一个平衡的哈希函数，它满足i符号sign( $f_{t}$ ( $x_{i}^{(t)}$ ))=0，将最大限度地增加x(t)[21]上的信息。下降符号函数，平衡约束将导致在=−iPtx(t)i/n，然后我们可以将方程（4）重写为ft(x(t))=Pt(x(t)−ix(it)/n)=Ptx(t)。但是，为了方便起见，我们仍然使用x(t)来表示中心数据x(t)。

总体目标函数结合了方程（6）中给出的集体矩阵分解部分，方程（4）中的线性嵌入部分和正则化项：

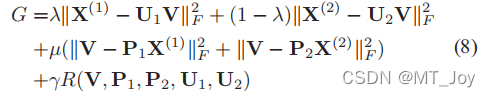
3.4学习哈希函数

优化问题（7）是非凸的，有五个矩阵变量U1、U2、P1、P2、v。幸运的是，在固定其他四个矩阵变量时，它对五个矩阵变量中的任何一个都是凸的。因此，优化问题可以通过按照列出的三个步骤迭代来解决，直到收敛。

5、结论

在本文中，我们提出了一种新的哈希方法，称为集体矩阵分解哈希，以实现对多模态数据的交叉查看相似性搜索。CMFH通过对一个实例的潜在因子模型的集体矩阵分解来学习统一的哈希码，这样就可以搜索到不同的视图。我们还证明了CMFH是一种具有近似双利普希茨连续性的保相似哈希方法。

我们进行了实验来验证所提出的CMFH的有效性。我们表明，在所有的交叉视图和大多数单视图相似度搜索实验中，CMFH取得了比几种最先进的哈希方法更好的性能。参数分析表明，CMFH对参数设置不敏感，在较大的参数值范围下具有显著的性能。此外，CMFH能够轻松地处理样本外实例，并且可以从大规模数据库的小训练集学习稳定的哈希函数，这使其适用于现实场景。

总结：