LQR控制算法及其仿真实现

---

1 离散有限时间系统

1.1 LQR问题描述

离散系统方程：
$$x_{t+1}=A_{n\times n}{x}_t+B_{n\times m}{u}_t,x_0=x^{init}$$
问题: 选取$u_0,u_1,\dots$使得：

• $x_0,x_1,\dots$较小，获得较好的状态控制；
• $u_0,u_1,\dots$较小，使用较少的输入控制；

较大的$u$可以使$x$快速趋于0。

定义二次代价函数：
$$J(U)=\sum _{\tau =0}^{N-1}(x_{\tau }^{T}Q{x}_{\tau }+u_{\tau }^{T}R{u}_{\tau })+x_N^T{Q}_f{x}_N$$
其中，$U=(u_0,u_1,\dots ,u_{N-1})$
$$Q=Q^T\ge 0,Q_f=Q_f^T\ge 0,R=R^T>0$$
分别为状态代价权重矩阵，终态代价权重矩阵和输入权重矩阵。

$N$为时间范围，可有限也可无限，后续分开讨论。

• $R>0$ 表示任何非零输入都会影响代价$J$

LQR问题：找到$u_0^{lqr},u_1^{lqr},\dots ,u_{N-1}^{lqr}$使$J$最小。

1.2 最小二乘法求解

令$X=[x_0^T,x_1^T,\dots ,x_N^T{]}^T,U=[u_0^T,u_1^T,\dots ,u_{N-1}^T{]}^T$，则有：
$$X_{Nn\times 1}={\left[\begin{array}{ccccccc}B& & 0& & \cdots & & 0\\ AB& & B& & \cdots & & 0\\ ⋮& & ⋮& & ⋮& & ⋮\\ A^{N-1}B& & A^{N-2}B& & \cdots & & B\end{array}\right]}_{Nn\times Nm}{U}_{Nm\times 1}+{\left[\begin{array}{c}A\\ ⋮\\ A^N\end{array}\right]}_{Nn\times n}{x}_0$$
写做：
$$X=GU+H{x}_0$$
则有：
$$J=U^T\tilde{R}U+X^T\tilde{Q}X=U^T\tilde{R}U+(GU+H{x}_0{)}^T\tilde{Q}(GU+H{x}_0)$$
其中$\tilde{R}=diag(\underset{N\text{个}}{\underbrace{R,R,\cdots ,R}})$，$\tilde{Q}=diag(\underset{N\text{个}}{\underbrace{Q,Q,\cdots ,Q}})$
$J$可以表示为关于$U$的二次型形式：
$$J(U)=U^T(\tilde{R}+G^T\tilde{Q}G)U+2x_0^T{H}^T\tilde{Q}GU+x_0^T{H}^T\tilde{Q}H{x}_0$$
可以证明求$J$的最小值是一个凸优化问题，可直接求导得到$J$取最小值时的$U$。
$$\frac{dJ}{dU}=2(\tilde{R}+G^T\tilde{Q}G)U+2G^T\tilde{Q}H{x}_0$$
令$\frac{dJ}{dU}=0$，则有
$$U^{\ast }=-(\tilde{R}+G^T\tilde{Q}G{)}^{-1}{G}^T\tilde{Q}H{x}_0$$

1.3 最小二乘法编程实现

以下为一个简单的例子：

%% Problem description:
% Suppose there is a car moving along the trajectory, and the current speed
%   is 0.1m/s. The current state of the car is that the lateral error is 0.5m, 
%   and the lateral error angle is 5 degrees. Now that the car wants to eliminate 
%   the lateral error by entering the angular velocity, we need to design the LQR
%   target and solve it.

% state function:
% [dx1, dx2]' = [0, v; 0, 0] * [x1, x2]' + [0, 1]' * u
% where x1 is the the lateral error, x2 is the the lateral error
%   angle, and u is the angular velocity
% Initial state: x1 = 0.5, x2 = 0.0872;
% End state: x1 = 0

%%
clear;clc;
close all;

A = [0, 0.1; 0, 0];
B = [0, 1]';
x0 = [0.5, 0.0872]';
[state_num, input_num] = size(B);

dt = 0.05;
N = 80/dt;

Ak = eye(2) + dt*A;
Bk = dt*B;

Q = eye(2);
R = 1;

% X = G * U + H * x0
G = zeros(N*state_num, N*input_num);
H = zeros(N*state_num, state_num);

tic;
for i = 1:N
    for j = 1:i
        G((state_num*(i-1)+1):(state_num*(i)), (input_num*(j-1)+1):(input_num*(j))) = Ak^(i-j)*Bk;
        H((state_num*(i-1)+1):(state_num*(i)), 1:state_num) = Ak^(i);
    end
end

H_q = diag(repmat(diag(R), N, 1)) + G'*diag(repmat(diag(Q), N, 1))*G;
f_q = x0'*H' * diag(repmat(diag(Q), N, 1)) *G;
U = - H_q \ f_q';
X = G*U+H*x0;
X1 = [x0(1); X(1:2:end-2)];
X2 = [x0(2); X(2:2:end-2)];
toc;

figure;
subplot(2, 1, 1);
hold on;
plot(X1, 'b');

subplot(2, 1, 2);
plot(X2, 'b');

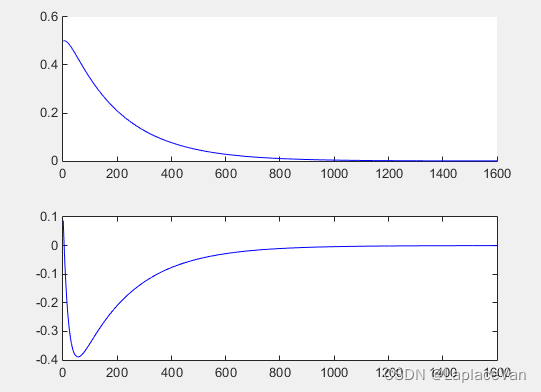
运行时间为71s，讲义里说明这种解法时间复杂度为$O(N^{3}n{m}^2)$，确实效率不高。

1.4 动态规划算法

定义函数$V_t:{\mathbf{R}}^n\to \mathbf{R}$
$$V_t(z)=\underset{u_t,\cdots ,u_{N-1}}{\min }\sum _{\tau =t}^{N-1}(x_{\tau }^{T}Q{x}_{\tau }+u_{\tau }^{T}R{u}_{\tau })+x_N^T{Q}_f{x}_N$$
满足$x_t=z,x_{\tau +1}=A{x}_{\tau }+B{u}_{\tau }$。则有一下几个性质：

• $V_t(z)$即为从$t$时刻，初始状态为$z$开始的LQR代价函数；
• $V_0(x_0)$为系统LQR代价函数；
• 可以证明$V_t$可以写成二次型形式，即$V_t(z)=z^T{P}_{t}z$，并且有$P_t=P_t\ge 0$；
• $P_t$可以从$t=N$开始反向递归求解；
• 最优控制$u$可以用$P_t$表示。

假设我们知道$V_{t+1}(z)$，需要选取$u_t$使得系统代价函数最小，$u_t$的选取会影响$u_t^{T}R{u}_t$，以及从下一个时刻开始的代价函数$V_{t+1}(Az+B{u}_t)$。
动态规划基本公式：
$$V_t(z)=\underset{w}{\min }(z^{T}Qz+w^{T}Rw+V_{t+1}(Az+Bw))$$
$w$即为使得$V_t(z)$取最小值的$u_t$。
根据上面的第三条性质，有：
$$V_{t+1}(Az+Bw)=(Az+Bw{)}^T{P}_{t+1}(Az+Bw)$$
代入上式可得：
$$V_t(z)=\underset{w}{\min }(z^{T}Qz+w^{T}Rw+(Az+Bw{)}^T{P}_{t+1}(Az+Bw))$$
同时也可以证明该问题为凸优化，最小值取在导数为0处。
$$\frac{d{V}_t}{dw}=2w^{T}R+2(Az+Bw{)}^T{P}_{t+1}B=0$$
可得：
$$w^{\ast }=-(R+B^T{P}_{t+1}B{)}^{-1}{B}^T{P}_{t+1}Az$$
则有：
$$\begin{array}{rl}{V}_t(z)& =z^{T}Qz+w^{\ast T}R{w}^{\ast }+(Az+B{w}^{\ast }{)}^T{P}_{t+1}(Az+B{w}^{\ast })\\ & =\cdots \\ & =z^T(Q+A^T{P}_{t+1}A-A^T{P}_{t+1}B(R+B^T{P}_{t+1}B{)}^{-1}{B}^T{P}_{t+1}A)z\\ & =z^T{P}_{t}z\end{array}$$
所以：
$$P_t=Q+A^T{P}_{t+1}A-A^T{P}_{t+1}B(R+B^T{P}_{t+1}B{)}^{-1}{B}^T{P}_{t+1}A$$
同时又有$P_N=Q_f$，所以可以根据时间序列反向求解$P_{N-1},P_{N-2},\cdots ,P_0$，根据$w^{\ast }$表达式可以顺序求解$u_t^{lqr}$。动态规划算法总结如下：

1. 令$P_N=Q_f$；
2. 对于$t=N,\cdots ,1$，$$P_{t-1}=Q+A^T{P}_{t}A-A^T{P}_{t}B(R+B^T{P}_{t}B{)}^{-1}{B}^T{P}_{t}A$$
3. 对于$t=0,\cdots ,N-1$，定义$$K_t=(R+B^T{P}_{t+1}B{)}^{-1}{B}^T{P}_{t+1}A$$
4. 对于$t=0,\cdots ,N-1$，最优控制为：$$u_t^{lqr}=K_t{x}_t$$

1.5 动态规划算法实现

问题描述：
两自由度，单输入单输出系统：
$$x_{t+1}=\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]x_t+\left[\begin{array}{c}0\\ 1\end{array}\right]u_t,y_t=\left[\begin{array}{cc}1& 0\end{array}\right]x_t$$
初始状态$x_0=(1,0),N=20$，权重矩阵：$Q=Q_f=C^{T}C,R=\rho I$，可取${\rho }_1=0.3,{\rho }_2=10$。

clear;clc;
close all;

A = [1,1;0,1];
B = [0;1];
C = [1,0];
x0 = [1;0];

N = 20;
Q = C'*C;
Q_f = Q;
rho = 0.3;
R = rho*eye(size(B, 2));

P = zeros(2, 2, N);
P(:,:,N) = Q_f;

for i = N-1:-1:1
    P(:,:,i) = Q+A'*P(:,:,i+1)*A-A'*P(:,:,i+1)*B/(R+B'*P(:,:,i+1)*B)*B'*P(:,:,i+1)*A;
end

K = zeros(1, 2, N);
u = zeros(1,N);
x = zeros(2, N);
x(:, 1) = x0;
y = zeros(1, N);

for i = 1:1:N-1
   K(:, :, i) = -(R+B'*P(:,:,i+1)*B)\B'*P(:,:,i+1)*A;
   u(i) = K(:,:,i)*x(:,i);
   x(:, i+1) = A*x(:, i)+B*u(i);
   y(i) = C*x(:, i);
end

figure(1);
subplot(2,2,1);
plot(u, '-ob');
hold on;grid on;
subplot(2,2,3);
plot(y, '-ob');
hold on;grid on;
K1 = reshape(K(1,1,:), 1, N);
K2 = reshape(K(1,2,:), 1, N);
subplot(2,2,2);
hold on;grid on;
plot(K1, '-b');
ylabel('K1');
subplot(2,2,4);
hold on;grid on;
plot(K2, '-b');
ylabel('K2');

%%
rho = 10;
R = rho*eye(size(B, 2));

P = zeros(2, 2, N);
P(:,:,N) = Q_f;

for i = N-1:-1:1
    P(:,:,i) = Q+A'*P(:,:,i+1)*A-A'*P(:,:,i+1)*B/(R+B'*P(:,:,i+1)*B)*B'*P(:,:,i+1)*A;
end

K = zeros(1, 2, N);
u = zeros(1,N);
x = zeros(2, N);
x(:, 1) = x0;
y = zeros(1, N);

for i = 1:1:N-1
   K(:, :, i) = -(R+B'*P(:,:,i+1)*B)\B'*P(:,:,i+1)*A;
   u(i) = K(:,:,i)*x(:,i);
   x(:, i+1) = A*x(:, i)+B*u(i);
   y(i) = C*x(:, i);
end

figure(1);
subplot(2,2,1);
plot(u, '-*r');
ylabel('u');
hold on;grid on;
legend('\rho = 0.3', '\rho = 10');
subplot(2,2,3);
plot(y, '-*r');
ylabel('y');
hold on;grid on;
legend('\rho = 0.3', '\rho = 10');

K1 = reshape(K(1,1,:), 1, N);
K2 = reshape(K(1,2,:), 1, N);
subplot(2,2,2);
hold on;grid on;
plot(K1, '-r');
ylabel('K1');
legend('\rho = 0.3', '\rho = 10');
subplot(2,2,4);
hold on;grid on;
plot(K2, '-r');
ylabel('K2');
legend('\rho = 0.3', '\rho = 10');

运行结果如下：

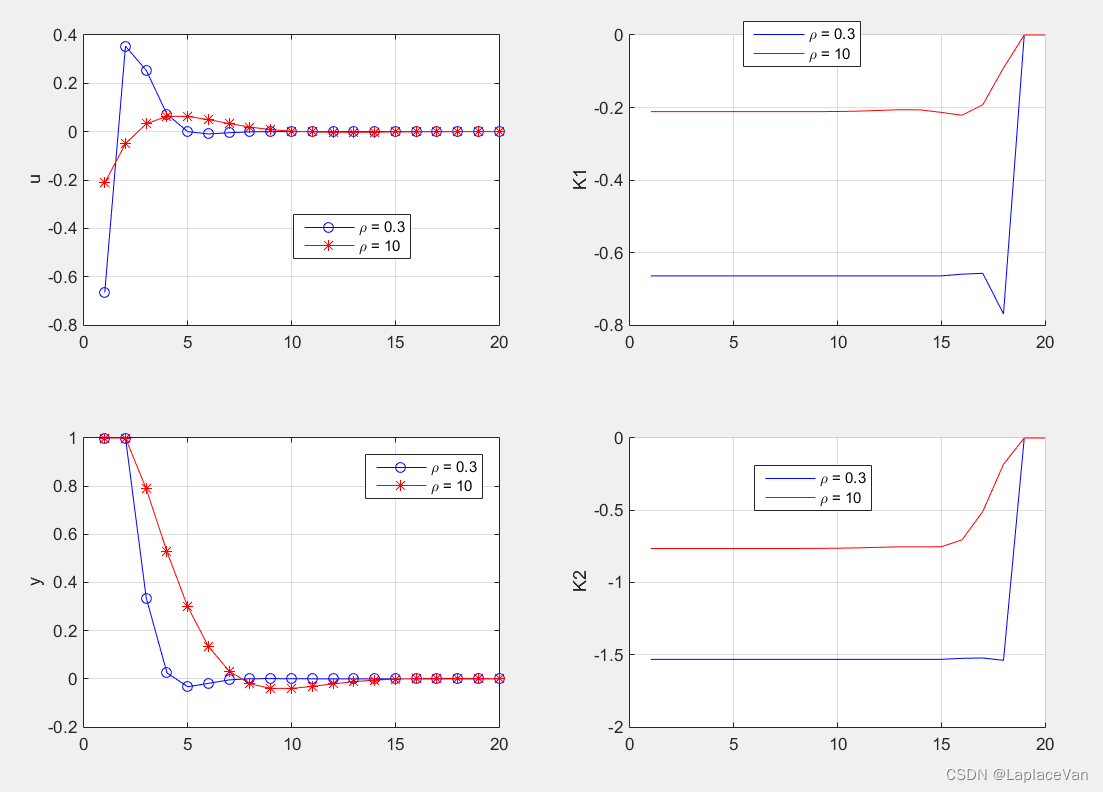
从上图结果可以发现，$K_t$从$t=0$开始一段时间内为恒定值，或者说$P_t$从$N$反向开始后很快就能收敛到恒定值。
即有：
$$P_{ss}=Q+A^T{P}_{ss}A-A^T{P}_{ss}B(R+B^T{P}_{ss}B{)}^{-1}{B}^T{P}_{ss}A$$
同时说明，对于不是很接近最终时刻的$t$时刻，LQR控制可以看作是一个线性定常反馈系统：
$$u_t=K_{ss}{x}_t,K_{ss}=-(R+B^T{P}_{ss}B{)}^{-1}{B}^T{P}_{ss}$$
这在实际中经常用到。
另外讲义中也提到，最终态的权重矩阵对反馈增益没有影响，即$P_t$的初始值对其收敛值没有影响：

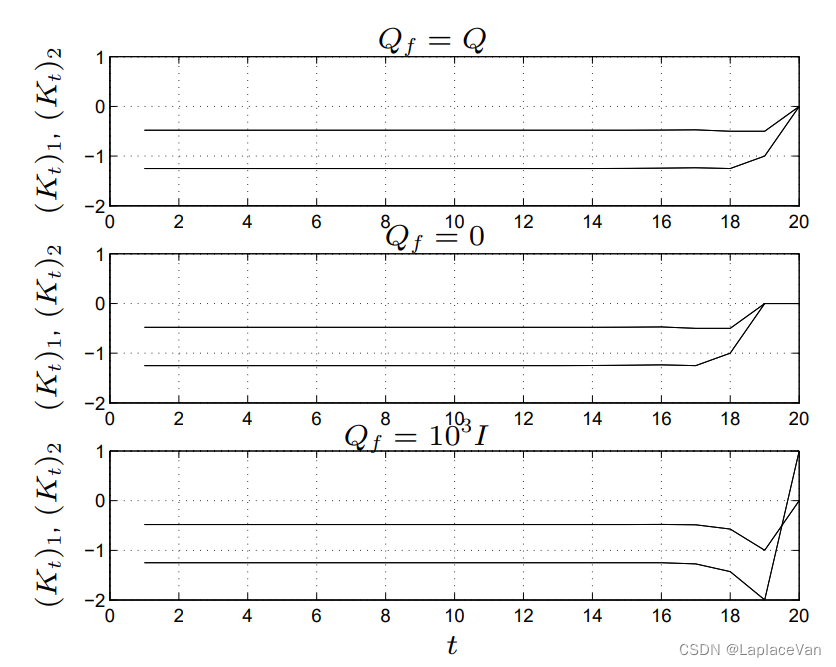
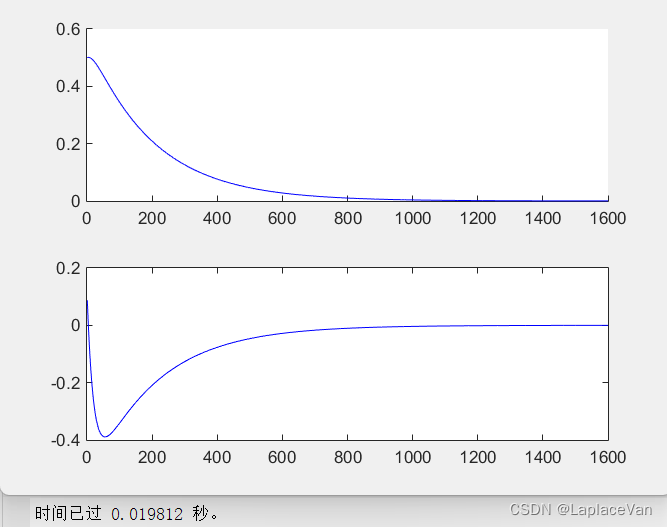
另外用DP方法求解第一个问题耗时不超过0.02s。

2 拉格朗日乘子法求解LQR

2.1 一些实用的矩阵特征

（1）
$$Z(I+Z{)}^{-1}=I-(I+Z{)}^{-1}$$
其中$(I+Z)$可逆。证明右边同乘$(I+Z)$即可。
（2）
$$(I+XY{)}^{-1}=I-X(I+YX{)}^{-1}Y$$
证明：
$$\begin{array}{rl}(I-X(I+YX{)}^{-1}Y)(I+XY)& =I+XY-X(I+YX{)}^{-1}Y(I+XY)\\ & =I+XY-X(I+YX{)}^{-1}(I+YX)Y\\ & =I+XY-XY=I\end{array}$$
（3）
$$Y(I+XY{)}^{-1}=(I+YX{)}^{-1}Y$$
证明左乘$(I+YX)$右乘$(I+XY)$即可。速记：左边$Y$移进去，右边$Y$移出来。
（4）
$$(I+X{Z}^{-1}Y{)}^{-1}=I-X(Z+YX{)}^{-1}Y$$
证明直接使用公式（2）即可。
（5）
$$(A+BC{)}^{-1}=A^{-1}-A^{-1}B(I+C{A}^{-1}B{)}^{-1}C{A}^{-1}$$
证明：
$$\begin{array}{rl}(A+BC{)}^{-1}& =(A(I+A^{-1}BC){)}^{-1}\\ & =(I+A^{-1}BC{)}^{-1}{A}^{-1}\\ & =(I-A^{-1}B(I+C{A}^{-1}B{)}^{-1}C)A^{-1}(使用公式(2))\\ & =A^{-1}-A^{-1}B(I+C{A}^{-1}B{)}^{-1}C{A}^{-1}\end{array}$$
（6）根据之前关于$P_t$的表达式可以进行化简：
$$\begin{array}{rl}{P}_t& =Q+A^T{P}_{t+1}A-A^T{P}_{t+1}B(R+B^T{P}_{t+1}B{)}^{-1}{B}^T{P}_{t+1}A\\ & =Q+A^T{P}_{t+1}(I-B(R+B^T{P}_{t+1}B{)}^{-1}{B}^T{P}_{t+1})A\\ & =Q+A^T{P}_{t+1}(I-B((I+B^T{P}_{t+1}B{R}^{-1})R{)}^{-1}{B}^T{P}_{t+1})A\\ & =Q+A^T{P}_{t+1}(I-B{R}^{-1}(I+B^T{P}_{t+1}B{R}^{-1}{)}^{-1}{B}^T{P}_{t+1})A\\ & =Q+A^T{P}_{t+1}(I+B{R}^{-1}{B}^T{P}_{t+1}{)}^{-1}A(使用公式(2))\\ & =Q+A^T(I+P_{t+1}B{R}^{-1}{B}^T{)}^{-1}{P}_{t+1}A\end{array}$$

2.2 线性约束最优化问题

$$\begin{array}{rl}min& f(x)\\ s.t.:& Fx=g\end{array}$$

• $f:{\mathbf{R}}^n\to \mathbf{R}$
• $F\in {\mathbf{R}}^{m\times n}$

拉格朗日表达式：
$$L(x,\lambda )=f(x)+{\lambda }^T(g-Fx)$$
其中，$\lambda$为拉格朗日乘子。若$x$是最优解，则有：
$${\nabla }_{x}L=\nabla f(x)-F^T\lambda =0,{\nabla }_{\lambda }L=g-Fx=0$$
即$\nabla f(x)=F^T\lambda$

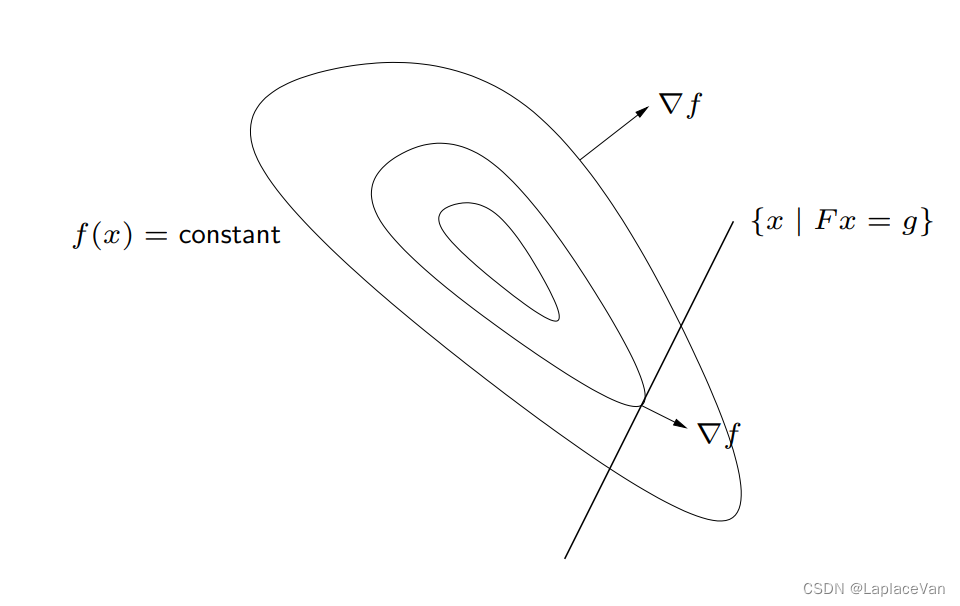
• 假设当前位置为$x$，为可行点，即$Fx=g$；
• 考虑沿$v$方向移动很小距离$h$，到达$x+hv$位置；
• 为了移动后仍为可行点，则需$F(x+hv)=g+hFv=g$，即$Fv=0$，所以$v\in \mathrm{N}(F)$，称为可行方向；
• 需要移动后得到更小目标函数：$$f(x+hv)\approx f(x)+h\nabla f(x{)}^{T}v<f(x)$$

当$\nabla f(x{)}^{T}v<0$时，为目标函数下降方向。当存在下降方向时，$x$不为最优解，所以当$x$为最优解时，应满足$\nabla f(x{)}^{T}v=0$

2.3 LQR约束最优化求解

把LQR问题写成最优化问题：
$$\begin{gathered} minJ=\frac{1}{2}\sum _{t=0}^{N-1}(x_t^{T}Q{x}_t+u_t^{T}R{u}_t)+\frac{1}{2}{x}_N^T{Q}_f{x}_N \\ s.t.x_{t+1}=A{x}_t+B{u}_t,t=0,1,\cdots ,N-1 \end{gathered}$$
则有拉格朗日表达式：
$$L=J+\sum _{t=0}^{N-1}{\lambda }_{t+1}(A{x}_t+B{u}_t-x_{t+1})$$
则有：
$$\begin{gathered} {\nabla }_{u_t}L=R{u}_t+B^T{\lambda }_{t+1}=0,u_t=-R^{-1}{B}^T{\lambda }_{t+1} \\ {\nabla }_{x_t}L=Q{x}_t+A^T{\lambda }_{t+1}-{\lambda }_t=0,{\lambda }_t=A^T{\lambda }_{t+1}+Q{x}_t \\ {\nabla }_{x_N}L=Q_f{x}_N-{\lambda }_N=0,{\lambda }_N=Q_f{x}_N \end{gathered}$$
对于原系统有：
$$x_{t+1}=A{x}_t+B{u}_t,x_0=x^{init}$$
迭代计算是从0时刻向后进行，初始条件为起始状态。
现在有：
$${\lambda }_t=A^T{\lambda }_{t+1}+Q{x}_t,{\lambda }_N=Q_f{x}_N$$
迭代计算从$N$时刻开始向前进行，初始条件为最终状态。
所以称$\lambda$为伴随状态，上式也称为伴随系统的状态方程。

可以用归纳法证明 ${\lambda }_t=P_t{x}_t$:
对于$t=N$，有${\lambda }_N=Q_f{x}_N$，现在假设${\lambda }_{t+1}=P_{t+1}{x}_{t+1}$成立，证明${\lambda }_t=P_t{x}_t$：
有：$${\lambda }_{t+1}=P_{t+1}(A{x}_t+B{u}_t)=P_{t+1}(A{x}_t-B{R}^{-1}{B}^T{\lambda }_{t+1})$$
所以：
$${\lambda }_{t+1}=(I+P_{t+1}B{R}^{-1}{B}^T{)}^{-1}{P}_{t+1}A{x}_t$$
所以：
$${\lambda }_t=A^T{\lambda }_{t+1}+Q{x}_t=A^T(I+P_{t+1}B{R}^{-1}{B}^T{)}^{-1}{P}_{t+1}A{x}_t+Q{x}_t=P_t{x}_t$$
其中$$P_t=Q+A^T(I+P_{t+1}B{R}^{-1}{B}^T{)}^{-1}{P}_{t+1}A$$与之前化简后结果一致。

持续更新中…

reference

• stanford EE363 Linear Dynamical Systems