论文翻译和解读 A Tutorial on Energy-Based Learning （一）

论文地址
这篇论文提出了一个概念Energy-based Models（EBMs）。由于原文篇幅较多，将分成多篇博客进行学习。

摘要

EBMs通过将每种配置的变量与一个标量（就是能量energy）相关联，来捕获变量之间的依赖关系。推理（Inference）阶段的工作是：固定观测变量，找到使得能量函数（energy function）最小的其他变量的配置。学习（Learning）阶段的工作是：找到一个能量函数，该函数能够使得观测到的变量配置具有低能量值，未观测到的变量配置具有高能量值。

作者可能意思是指：找到一个能量函数，能够让已知正确的变量配置具有低能量值，让错误变量配置具有高能量值。

EBM方法为很多学习模型提供了一个通用的理论框架，包括传统的判别模型和生成模型，以及graph-transformer网络，条件随机场，最大间隔马尔可夫网络以及多种流学习方法（manifold learning methods）。
概率模型必须能够很好地被正则化，这通常情况下需要计算所有可能的变量配置上的积分，而这个积分一般是非常棘手的。由于EBMs不需要正则化步骤，这个问题也就很好地被规避了。EBMs可以被视为一种非概率因子图（non-probabilistic factor graph），在体系结构和训练准则的设计上比概率方法提供了相当大的灵活性。

1.简介

统计建模和机器学习的主要目的是编码变量之间的依赖关系。通过捕获这些依赖关系，一个模型可以用于在给定了已知变量的情况下，回答未知变量值。

EBMs通过关联每种变量配置和一个标量的能量值（可以看成一种兼容性的度量），来捕捉上文提到的依赖关系。推理（Inference）阶段做出预测或决策：给定了观测变量的值，寻找使得能量函数最小的其他变量的值；学习（Learning）阶段找到一个能量函数：该能量函数能够将低能量值关联到其他变量的正确的值，高能量值关联到不正确的值；损失函数（A loss functional）：在学习（Learning）阶段最小化，用来衡量能量函数的质量。在这样一个普通的推理/学习框架中，有很多可供选择的能量函数和损失函数，从而可以设计多样的统计模型，包括概率的和非概率的。

基于能量的学习为多种概率的或非概率的方法提供了同一的框架进行学习，特别是概率图的非概率学习和其他的结构化的模型。基于能量的学习可以看成用于预测、分类或者决策问题的概率估计的一种替代方案。因为不需要合适的正则化，基于能量的方法避免了在概率模型中估计正则化参数（normalization constant）的问题。另外，不需要正则化的处理使得学习机制的设计更加灵活。大多数概率模型可以被看做EBMs的一个特别的类型，其中，能量函数满足某种特定的正则化条件，且损失函数也有着某种特别的形式。

下面是这篇论文的文章结构安排：

1. 第一章介绍EBMs和通过最小化能量函数的判别式推理；
2. 第二章介绍基于能量的学习以及损失函数的概念。描述了多种标准的和非标准的损失函数，包括感知器损失（perceptron loss）、多种基于margin的损失以及负对数似然损失。负对数似然函数可以用于训练一个模型产生条件概率估计；
3. 第三章展示了如何将简单的回归和分类模型规范化为EBM框架；
4. 第四章关注了包含隐变量的EBMs；
5. 第五章详细地分析了多种损失函数，并且给出了损失函数必须满足的充分条件，这样才能使得使其最小化能够使得模型接近人们期待的行为；

疑惑：必须满足的不应该是必要条件吗，后面介绍的好像说的是充分条件，但不是必要条件，也就是不一定必须满足……

6. 第六章介绍了非概率因子图的概念，并且讨论了高效的推理算法；
7. 第七章关注于序列化标记和结构化输出的模型。在EBM框架下重新构造了最大边际Markov网络和条件随机场等线性模型。回顾了上世纪80 90年代的语音和手写识别的判别式学习，这包括集成非线性判别函数的全局训练系统，如神经网络，以及序列比对方法，如动态时间规整和隐马尔可夫模型。并对graph-transformer网络结构等分层模型进行了评述；
8. 基于能量的方法、概率的方法和基于采样的近似方法（如contrastive divergence）的区别、共性和相对优势。

1.1 Energy-Based Inference（基于能量的推断）

上图是一个EBM的例子，用能量函数$E(X,Y)$衡量观测变量$X$和待预测变量$Y$之间的相容性。例如$X$是一幅图片，$Y$是一个离散变量，表示图片的类别。给定$X$时，这个模型产生了使得能量函数$E(X,Y)$最小化的答案$Y$。

现在我们来考虑一个模型，如上图有两个变量集合：$\mathcal{X}$和$\mathcal{Y}$，变量$X\in \mathcal{X}$是一个向量，包含某个物体图片的像素，变量$Y\in \mathcal{Y}$是一个离散变量，描述了该物体是什么可能的类别。例如$\mathcal{Y}$包含六个可能的值：动物、人体形态、飞机、货车、汽车以及都不是。这个模型可以看成一个能量函数，衡量每个可能的$X$和$Y$的配置的好坏。输出的数字可以被解读为$X$和$Y$之间的兼容程度。接下来，我们使用这样一个约定：小能量值对应着变量的高兼容性的配置，大能量值对应着变量的高不兼容性的配置。这种函数在不同的技术场景中被给定了不同的名字：也许会叫做对比函数（contrast functions）、值函数（value functions）或者负对数似然函数。接下来，我们将使用能量函数（energy function）$E(X,Y)$来表示。我们需要注意，能量函数和损失函数的区别：能量函数是在推理（inference）阶段最小化的，而损失函数是在学习（learning）阶段最小化的。

在大多数常见的模型使用中，给定$X$，模型产生了与观测值$X$最匹配的答案$Y$，更精确地说，就是这个模型模型必须产生一个值$Y^{\ast }$，该值属于$\mathcal{Y}$集合，使得$E(X,Y)$最小。
$$Y^{\ast }=argmi{n}_{Y\in \mathcal{Y}}(E(X,Y))$$如果集合$\mathcal{Y}$很小，我们可以对于任何的$Y$都计算出$E(X,Y)$，然后选择最小的。

然而实际上，选择最好的$Y$也许并不会这么简单。

上图提供了多种场景，在这些场景中$\mathcal{Y}$很大，以至于穷举搜索并不实际。模型(a)用于面部识别，$\mathcal{Y}$是离散且有限的，但其基数也许是成千上万的。（b）用于在图片中找到人脸，并且估计这些人脸的位置，此时$\mathcal{Y}$包含两种值，其中一个是二进制值，每个表示对应的位置是否有面部信息，另一个是一系列连续值，表示面部信息的尺寸和范围。（不翻译了，这一段都是举例子。）

对上述场景，一个特别的策略，叫做“inference procedure”（推理过程），用于找到使得$E(X,Y)$最小的$Y$值。在很多实际的场景中，对于给定$X$，推理过程将会产生一个近似的最小化的$E(X,Y)$，可能是也可能不是全局最优解。事实上，可能存在$E(X,Y)$有多个最小值的情况，最好的推理过程取决于模型内部结果。例如：

• 如果$\mathcal{Y}$是连续值，且$E(X,Y)$相对于$Y$是光滑且表现良好的，我们也许可以使用基于梯度的算法。
• 如果$\mathcal{Y}$是一个离散值的聚合，能量函数可以表示成一个factor graph（因子图），能量函数的和依赖于不同的变量子集。我们可以使用因子图的高效的推理过程，如min-sum。
• 当每个$\mathcal{Y}$的元素可以被表示成带权有向无环的图上的一个路径，特定$Y$的能量函数便是该值对应的路径上的边和节点值的和。这种场景常常会发生在序列标记问题如语音识别，手写识别，自然语言处理以及生物序列分析中。

不同的情况可能需要使用其他优化程序，包括连续优化方法，如线性规划、二次规划、非线性优化方法，或离散优化方法，如模拟退火、图切割或图匹配。在许多情况下，精确的优化是不切实际的，我们必须求助于近似方法，包括使用替代能量函数的方法（如变分方法）。

1.2 这样一个模型可以回答什么问题呢

在前面的讨论中，我们已经暗示了模型要回答的问题是：“哪个$Y$与$X$最匹配？”，这个场景发生在预测、分类或者决策任务中。然而，一个模型也许可以回答多种类型的问题：

1. 预测，分类和决策：“哪个$Y$与$X$最匹配？” 这个场景将会发生在当模型用于做一个艰难的决策时或者产生一个动作时，例如模型用于驱动一个机器人并且避免障碍，它必须要产生一个最好的决策比如“左转”，“右转”，“直走”。
2. 排序：“$Y_1$和$Y_2$哪个和$X$更匹配？” 这是一个比分类更复杂点的问题，因为系统必须训练以产生所有答案的完整排序，而不是只产生最好的那个。这种场景发生于很多数据挖掘应用中，模型用于筛选出多个满足给定准则的样本。
3. 检测任务：“$Y$值和$X$匹配吗？”典型的检测任务如检测图片中的人脸，比较一个人脸类别与阈值。因为通常在系统建立时阈值是未知的，因此这个系统必须被训练，使得随着图片看起来不像人脸的程度增加，能量值也会增加。
4. 条件密度估计：给定$X$时$Y$满足什么样的条件概率分布呢？”这个场景在：当系统的输出不是用于直接产生决策，而是提供给人类决策者，或者输入另一个单独构建的系统。

通常我们认为$X$是一个高维变量，$Y$是一个离散变量，但相反的情况也是常见的。当一个模型用于图像重建，计算机图形学，语音和语言生成等应用中就会出现这种情况。最常见的情况是$X$和$Y$都是高维的。

1.3 Decision Making versus Probabilistic Modeling

对于决策任务，例如操作机器人，需要系统对正确的答案给出一个最低的能量，只要其他能量的值更大，它们便无足轻重。但一个系统的输出有时必须和另一个系统的输出结合，或者输入另一个系统（或者提供给人类决策者）。由于能量值没有标定（即以任意单位进行度量），将两个单独训练的EBM结合起来并不简单：没有先验保证它们的能量值尺度是一致的。校准能量使得这样的结合可以通过多种方式完成。然而，唯一一致的方法是将所有可能输出的能量集合变成归一化的概率分布。将能量值转化为0-1之间的值，且总和为1的最简单、最常用的方法就是通过Gibbis分布：
$$P(Y|X)=\frac{e^{-\beta E(Y,X)}}{{\int }_{y\in \mathcal{Y}}{e}^{-\beta E(Y,X)}}$$其中$\beta$是一个任意的正实数，类似于逆温度。分母叫配分函数。Gibbis分布的选择也许看起来很随意，但其他的概率分布都可以通过能量函数$E(X,Y)$一个很好的重定义来获得（或者近似获得）。这种方法获取的数据是否是好的，不取决于能量如何转化为概率，而是取决于如何从数据中估计能量值$E(X,Y)$。

需要注意的是，上述能量到概率的转化只有当分母${\int }_{y\in \mathcal{Y}}{e}^{-\beta E(Y,X)}$是收敛的时候才有可能。这一定程度上限制了可以使用的能量函数和$\mathcal{Y}$。更重要的是，很多实际的场景下，计算配分函数是不切实际的（比如当$\mathcal{Y}$基数很大），或者直接不可能（比如$\mathcal{Y}$包含的是高维变量，并且这个积分没有可以解决的办法）。因为概率建模具有很大的成本，当应用不需要时应该被避免。

2.Energy-Based Training: Architecture and Loss Function

训练一个EBM在于找到一个能量函数，能够对任何$X$产生最好的$Y$，寻找最好的能量函数在一个能量函数簇$\mathcal{E}$中进行，该簇中的元素以参数$W$为索引。
E = { E ( W , X , Y ) : W ∈ W } \mathcal{E}=\{E(W,X,Y): W\in W\} E={E(W,X,Y):W∈W}EBM的结构是参数化的能量函数$E(W,X,Y)$的内部结构。此时，我们对$X$，$Y$，$W$和$E$的性质没有特别的限制。当$X$和$Y$是实数向量时，$\mathcal{E}$可以是简单的线性基函数集合，或者是一系列神经网络结构。第三章给出了常见的分类和回归的应用例子。当$X$和$Y$是可变大小的图像、符号或者向量的序列，或者更复杂的结构化实体，$\mathcal{E}$也许展示一个更丰富的函数类。第四、六、七章讨论了多种这样架构的例子。基于能量方法的一个优点是对$\mathcal{E}$的性质限制很小。

为了训练模型进行预测、分类或者决策，我们给定了一系列训练样本 S = { ( X i , Y i ) : i = 1 … P } S=\{(X^i,Y^i): i=1\ldots P\} S={(Xi,Yi):i=1…P}，当$X^i$是第$i$个训练样本的输入，$Y^i$是对应的理想的输出。为了在$\mathcal{E}$中找到最好的能量函数，我们需要有一种方法来获取任何一个特定的能量函数的质量，这基于两个元素：训练集和我们关于这个任务的先验知识。这个质量度量就叫做能量函数（loss functional），表示为$L(E,S)$。为了简化，我们通常表示为$L(W,S)$。学习任务就是简单的找到$W$使得该损失函数最小：
$$W^{\ast }=mi{n}_{W\in W}L(W,S)$$对于大多数场景，损失函数被表示为：
$$L(E,S)=\frac{1}{P}\sum _{i=1}^{P}L(Y^i,E(W,\mathcal{Y},X^i))+R(W)$$此时会在训练集上计算每个样本的损失函数值并求和。单个样本的损失函数值表示为$L(Y^i,E(W,\mathcal{Y},X^i))$（文中称为per-sample loss functional），依赖于目标答案$Y^i$和固定输入样本变化答案$Y$获取的能量值。因此，对于每个样本，我们估计了一个能量表面的切片。

能量表面的切片是什么意思？？？

$R(W)$是正则项，可以用来嵌入我们关于能量函数簇中哪个能量函数比其他的能量函数好的先验知识。有了这个定义，损失值在训练样本的排列下和训练集的多次重复下是不变的。

自然，学习的最终目的是为了产生一个模型，对训练过程中没有看到的新输入样本给出很好的答案，我们可以依赖于统计学习理论中的一般结果来保证，在简单的样本上的可交换性的条件下，以及通常的能量函数簇上的条件下，在训练集上最小化的损失值和在一个大的、独立的测试集上的损失值受到一个量的限制，这个量随着训练集样本数的增大，而逐渐收敛到0。

Designing a Loss Functional

直观地说，per-sample loss functional的设计方式应该是，它将低损失值分配给行为良好的能量函数，行为良好的能量函数应该是这样的：给正确答案提供最低能量和给所有其他(不正确)答案提供更高能量。相反，能量函数给正确答案以最高能量而给错误答案以最低能量，将会具有很高的损失。下文将进一步讨论损失函数(选择最佳能量函数的损失函数)的适当性。

只考虑训练一个模型来回答预测、分类以及决策问题，基于能量的方法的主要直觉如下（啥叫直觉，不知道怎么翻译好）：训练一个EBM在于构建一个能量函数，可以对于任何一个给定的$X$，推理算法将会产生我们理想的$Y$。由于推理算法选择最低能量的$Y$，学习过程必须调整能量表面，使得理想的$Y$值具有相比其他所有值最低的能量值。

下面给出了两个图，这两个图分别展示了对于给定输入样本$X^i$，当$Y$是离散变量和连续变量时的能量。


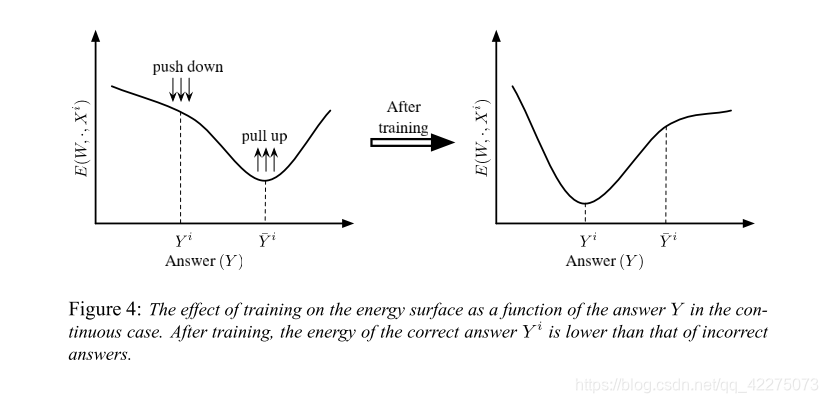
在这两幅图中，有三种类别的答案：

• $Y^i$：正确的答案；
• $Y^{\ast i}$：模型产生的答案，也就是最低能量的答案；
• ${\overline{Y}}^i$：the most offending incorrect answer，在错误的答案中，具有最低能量值的答案。为了在连续的场景中（$\mathcal{Y}$是连续的）定义这个类别的答案，我们可以简单地认为与$Y^i$距离在$ϵ$之内的都是正确的，所有距离超过$ϵ$都是错误的。

很好地定义损失函数后，学习过程应该拉低$E(W,Y^i,X^i)$，并且拉高所有错误答案的值，特别是$E(W,{\overline{Y}}^i,X^i)$。不同的损失函数通过不同的方式来完成这个过程。第5章将会给出一个损失函数满足的充分条件，保证了能量表面是被正确地塑造了。我们发现了一些广泛使用的损失函数不满足这个条件，同时也有其他的损失函数满足。

总结：给定一个训练集$S$，构建和训练一个基于能量的模型（EBM）需要设计下面四个组件：

1. 架构：能量函数$E(W,Y,X)$的内部结构；
2. 推理算法：一个方法，能够使得对任意给定的$X$，找到最小化$E(W,Y,X)$的$Y$值；
3. 损失函数：$L(W,S)$，使用训练集度量能量函数的质量；
4. 学习算法：一个方法，给定一个训练集，在能量函数簇$\mathcal{E}$中找到一个$W$，该$W$值使得损失函数最小。

合理的设计架构和损失函数是非常重要的。我们拥有的任何关于该任务的先验知识都被嵌入到架构和损失函数（特别是正则项）中。不幸的是，不是所有架构和损失函数的结合都是被允许的。一些结合中，最小化损失函数并不能使得模型产生最好的答案。选择可以有效、高效学习的架构和损失函数的结合对于一个基于能量的方法是非常重要的，因此是这篇论文的主要议题。